3-اتم هیدروژن
تابع موج [ ویرایش ]
همیلتونی اتم هیدروژن عملگر انرژی جنبشی شعاعی و نیروی جاذبه کولن بین پروتون مثبت و الکترون منفی است . با استفاده از معادله شرودینگر مستقل از زمان، نادیده گرفتن تمام فعل و انفعالات اتصال اسپین و استفاده از جرم کاهش یافته 
بسط لاپلاسین در مختصات کروی:
این یک معادله دیفرانسیل جزئی قابل تفکیک است که بر حسب توابع خاص قابل حل است. وقتی تابع موج به عنوان حاصلضرب توابع جدا می شود


- شعاعی:
- قطبی:
- آزیموت:
توابع موج موقعیت نرمال شده ، که در مختصات کروی آورده شده اند عبارتند از:
تصویر سه بعدی از حالت ویژه
جایی که :
- ∗
،
- ∗
کاهش شعاع بور است ،
،
یک چند جمله ای تعمیم یافته لاگر درجه است
، و
تابع هارمونیک کروی درجه است
و مرتبه
. توجه داشته باشید که چند جمله ای های لاگر تعمیم یافته توسط نویسندگان مختلف به طور متفاوتی تعریف شده اند. استفاده در اینجا با تعاریف استفاده شده توسط مسیحا، [7] و ریاضی سازگار است. [8] در جاهای دیگر، چند جملهای لاگر شامل یک عامل است
، [9] یا چند جمله ای تعمیم یافته لاگر که در تابع موج هیدروژن ظاهر می شود
بجای. [10]
اعداد کوانتومی می توانند مقادیر زیر را بگیرند:
( عدد کوانتومی اصلی )
( عدد کوانتومی ازیموتال )
( عدد کوانتومی مغناطیسی ).
علاوه بر این، این توابع موج نرمال می شوند (یعنی انتگرال مربع مدول آنها برابر با 1 است) و متعامد :




توابع موج در فضای تکانه با توابع موج در فضای موقعیت از طریق تبدیل فوریه مرتبط هستند.
که برای حالتهای محدود، منجر به [12] میشود.
جایی که 


راهحلهای معادله شرودینگر برای هیدروژن تحلیلی هستند و بیانی ساده برای سطوح انرژی هیدروژن و بنابراین فرکانسهای خطوط طیفی هیدروژن میدهند و مدل بور را به طور کامل بازتولید میکنند و فراتر از آن میروند. همچنین دو عدد کوانتومی دیگر و شکل تابع موج الکترون («اوربیتال») را برای حالتهای مکانیکی کوانتومی ممکن به دست میدهد، بنابراین ویژگی ناهمسانگرد پیوندهای اتمی را توضیح میدهد.
معادله شرودینگر برای اتمها و مولکولهای پیچیدهتر نیز کاربرد دارد . هنگامی که بیش از یک الکترون یا هسته وجود دارد، راه حل تحلیلی نیست و یا محاسبات کامپیوتری ضروری است یا فرضیات سادهسازی باید انجام شود.
از آنجایی که معادله شرودینگر فقط برای مکانیک کوانتومی غیر نسبیتی معتبر است، راه حل هایی که برای اتم هیدروژن به دست می دهد کاملاً صحیح نیستند. معادله دیراک نظریه کوانتومی نسبیتی این راه حل ها را بهبود می بخشد (به زیر مراجعه کنید).

![{\displaystyle -{\frac {\hbar ^{2}}{2\mu }}\left[{\frac {1}{r^{2}}}{\frac {\partial }{\partial r} }\left(r^{2}{\frac {\partial \psi }{\partial r}}\right)+{\frac {1}{r^{2}\sin \theta }}{\frac { \partial }{\partial \theta }}\left(\sin \theta {\frac {\partial \psi }{\partial \theta }}\right)+{\frac {1}{r^{2}\ sin ^{2}\theta }}{\frac {\partial ^{2}\psi }{\partial \varphi ^{2}}}\right]-{\frac {e^{2}}{4\ pi \varepsilon _{0}r}}\psi =E\psi }](https://wikimedia.org/api/rest_v1/media/math/render/svg/fed150abb1693ab2493937b669446a54865b9562)




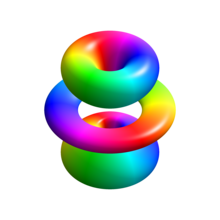


 در این وبلاگ به ریاضیات و کاربردهای آن و تحقیقات در آنها پرداخته می شود. مطالب در این وبلاگ ترجمه سطحی و اولیه است و کامل نیست.در صورتی سوال یا نظری در زمینه ریاضیات دارید مطرح نمایید .در صورت امکان به آن می پردازم. من دوست دارم برای یافتن پاسخ به سوالات و حل پروژه های علمی با دیگران همکاری نمایم.در صورتی که شما هم بامن هم عقیده هستید با من تماس بگیرید.
در این وبلاگ به ریاضیات و کاربردهای آن و تحقیقات در آنها پرداخته می شود. مطالب در این وبلاگ ترجمه سطحی و اولیه است و کامل نیست.در صورتی سوال یا نظری در زمینه ریاضیات دارید مطرح نمایید .در صورت امکان به آن می پردازم. من دوست دارم برای یافتن پاسخ به سوالات و حل پروژه های علمی با دیگران همکاری نمایم.در صورتی که شما هم بامن هم عقیده هستید با من تماس بگیرید.