تاریخچه [ ویرایش ]

فیلسوف یونان باستان زنون ایلیا مشکل جمع کردن یک سری نامتناهی را برای رسیدن به یک نتیجه متناهی در نظر گرفت، اما آن را غیرممکن رد کرد. [2] نتیجه پارادوکس زنو بود . بعدها، ارسطو یک راه حل فلسفی برای پارادوکس پیشنهاد کرد، اما محتوای ریاضی ظاهراً حل نشده بود تا زمانی که ارشمیدس آن را مطرح کرد، همانطور که قبل از ارسطو توسط دموکریتوس اتمیست پیشسوکرات بود . از طریق روش فرسودگی ارشمیدس بود که می‌توان تعداد نامحدودی از تقسیم‌بندی‌های پیشرونده را برای دستیابی به یک نتیجه محدود انجام داد. [3] لیو هوی به طور مستقل از روش مشابهی چند قرن بعد استفاده کرد. [4]

در قرن چهاردهم، اولین نمونه‌های سری خاص تیلور (اما نه روش عمومی) توسط مادهاوا از Sangamagrama ارائه شد . [5] [6] اگرچه هیچ سابقه‌ای از کار او باقی نمانده است، نوشته‌های پیروانش در مکتب نجوم و ریاضیات کرالا نشان می‌دهد که او سری تیلور را برای توابع مثلثاتی سینوس ، کسینوس و تتانژانت پیدا کرده است (به سری مدهاوا مراجعه کنید ). در طول دو قرن بعد، پیروان او بسط های سری و تقریب های عقلانی بیشتری را توسعه دادند.

در اواخر سال 1670، جیمز گرگوری در نامه‌ای از جان کالینز چندین سری مکلارین نشان داده شد .⁡،{\textstyle \sin x,} cos⁡، {\textstyle \cos x,}،{\textstyle \arcsin x,}و{\textstyle x\cot x}) توسط ایزاک نیوتن مشتق شده است و گفته می شود که نیوتن یک روش کلی برای بسط توابع در سری ایجاد کرده است. نیوتن در واقع از روشی دست و پا گیر استفاده کرده بود که شامل تقسیم طولانی سری ها و انتگرال ترم به ترم بود، اما گرگوری آن را نمی دانست و به دنبال کشف یک روش کلی برای خود شد. در اوایل سال 1671، گرگوری چیزی شبیه به سری کلی مکلارین را کشف کرد و نامه‌ای برای کالینز ارسال کرد که شامل مجموعه‌هایی برای ،{\textstyle \tan x,} ⁡،{\textstyle \sec x,} ⁡{\textstyle \ln \,\sec x}(انتگرال از\ قهوهای مایل به زرد) لوگاریتم {\textstyle \ln \,\tan {\tfrac {1}{2}}{{\bigl (}{\tfrac {1}{2}}\pi +x{\bigr )}}}( انتگرال sec ، تابع گودرمن معکوس )،arcsec⁡(2ه)،{\textstyle \operatorname {arcsec} {\bigl (}{\sqrt {2}}e^{x}{\bigr )}،}و{\textstyle 2\arctan e^{x}-{\tfrac {1}{2}}\pi }(عملکرد گودرمانی). با این حال، گرگوری با این فکر که او صرفاً روشی را توسط نیوتن دوباره توسعه داده است، هرگز توضیح نداد که چگونه این مجموعه ها را به دست آورده است، و تنها می توان استنباط کرد که او با بررسی کارهای خراشیده ای که در پشت نامه دیگری از سال 1671 نوشته بود، روش کلی را درک کرد. [7]

در سال‌های 1691-1692، آیزاک نیوتن بیانیه‌ای صریح از سری تیلور و مکلارین را در نسخه‌ای منتشر نشده از کار خود De Quadratura Curvarum نوشت . با این حال، این کار هرگز تکمیل نشد و بخش‌های مربوطه از بخش‌هایی که در سال 1704 تحت عنوان Tractatus de Quadratura Curvarum منتشر شد حذف شد .

تا اینکه در سال 1715 یک روش کلی برای ساخت این سری‌ها برای همه توابعی که برای آنها وجود دارند، سرانجام توسط بروک تیلور منتشر شد ، [8] که این سری‌ها اکنون به نام او نامگذاری شده‌اند.

نام مجموعه مکلورن به افتخار کالین مکلارین ، استادی در ادینبورگ، که مورد خاص نتیجه تیلور را در اواسط قرن 18 منتشر کرد، نامگذاری شد.

توابع تحلیلی [ ویرایش ]

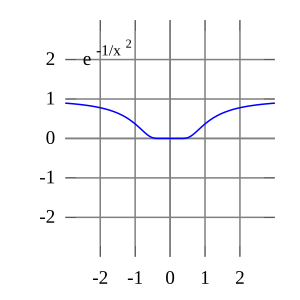
تابع e (-1/ x2 ) در x = 0 تحلیلی نیست : سری تیلور یکسان 0 است، اگرچه تابع نیست.

مقاله اصلی: تابع تحلیلی

اگر f  ( x ) توسط یک سری توان همگرا در یک دیسک باز با مرکز b در صفحه مختلط (یا بازه ای در خط حقیقی) داده شود، گفته می شود که در این ناحیه تحلیلی است. بنابراین برای x در این ناحیه، f توسط یک سری توان همگرا به دست می آید

.f(x)=\sum _{n=0}^{\infty }a_{n}(xb)^{n}.

با x متمایز کردن فرمول بالا n بار، سپس با تنظیم x = b به دست می آید:

{\frac {f^{(n)}(b)}{n!}}=a_{n}

و بنابراین بسط سری قدرت با سری تیلور مطابقت دارد. بنابراین یک تابع در یک دیسک باز با مرکز b تحلیلی است اگر و تنها در صورتی که سری تیلور آن به مقدار تابع در هر نقطه از دیسک همگرا شود.

اگر f  ( x ) برابر با مجموع سری تیلور آن برای تمام x در صفحه مختلط باشد، کل نامیده می شود . چند جمله ای ها، تابع نمایی ex ، و توابع مثلثاتی سینوس و کسینوس، نمونه هایی از کل توابع هستند. نمونه هایی از توابع که کامل نیستند عبارتند از: جذر ، لگاریتم ، مماس تابع مثلثاتی ، و معکوس آن، تان . برای این توابع اگر x از b دور باشد ، سری تیلور همگرا نمی شوند . یعنی اگر فاصله بین x و b بزرگتر از شعاع همگرایی باشد، سری تیلور در x واگرا می شود . اگر مقدار تابع و همه مشتقات آن در یک نقطه مشخص باشد، می‌توان از سری تیلور برای محاسبه مقدار کل تابع در هر نقطه استفاده کرد.

موارد استفاده از سری تیلور برای توابع تحلیلی عبارتند از:

  1. مجموع جزئی ( چند جمله ای های تیلور ) سری را می توان به عنوان تقریبی از تابع استفاده کرد. این تقریب ها در صورتی خوب هستند که اصطلاحات به اندازه کافی گنجانده شوند.
  2. تمایز و انتگرال سری های توانی را می توان به صورت ترم انجام داد و از این رو بسیار آسان است.
  3. یک تابع تحلیلی به طور منحصر به فردی به یک تابع هولومورفیک در یک دیسک باز در صفحه مختلط گسترش می یابد . این باعث می شود که ماشین تجزیه و تحلیل مختلط در دسترس باشد.
  4. سری (قطع شده) را می توان برای محاسبه مقادیر توابع به صورت عددی استفاده کرد (اغلب با ریختن مجدد چند جمله ای به شکل چبیشف و ارزیابی آن با الگوریتم کلنشاو ).
  5. عملیات جبری را می توان به راحتی بر روی نمایش سری توان انجام داد. برای مثال، فرمول اویلر از بسط های سری تیلور برای توابع مثلثاتی و نمایی پیروی می کند. این نتیجه در زمینه هایی مانند تحلیل هارمونیک از اهمیت اساسی برخوردار است .
  6. تقریب با استفاده از چند عبارت اول یک سری تیلور می تواند مشکلات غیر قابل حل را برای یک دامنه محدود ممکن کند. این روش اغلب در فیزیک استفاده می شود.

خطای تقریب و همگرایی [ ویرایش ]

مقاله اصلی: قضیه تیلور

تابع سینوس (آبی) با چند جمله ای تیلور درجه 7 (صورتی) برای یک دوره کامل در مرکز مبدأ تقریباً تقریب دارد.

چند جمله ای های تیلور برای ln(1 + x ) فقط تقریب های دقیقی را در محدوده −1 < x≤ 1 ارائه می دهند . برای x > 1 ، چند جمله ای های تیلور با درجه بالاتر تقریب بدتری ارائه می دهند.

تقریب های تیلور برای ln(1 + x ) (سیاه). برای x > 1 ، تقریب ها واگرا می شوند.

تصویر تقریب دقیق sin x حول نقطه x = 0 است . منحنی صورتی یک چند جمله ای درجه هفت است:

.{\displaystyle \sin {x}\approx x-{\frac {x^{3}}{3!}}+{\frac {x^{5}}{5!}}-{\frac {x^ {7}}{7!}}.\!}

خطا در این تقریب بیشتر از | نیست x | 9/9  ! . برای یک چرخه کامل در مرکز مبدا ( -π < x < π ) خطا کمتر از 0.08215 است. به طور خاص، برای -1 < x < 1 ، خطا کمتر از 0.000003 است.

در مقابل، همچنین تصویری از تابع لگاریتم طبیعی ln(1 + x ) و برخی از چندجمله ای های تیلور آن در اطراف a = 0 نشان داده شده است . این تقریب ها فقط در ناحیه -1 < x ≤ 1 به تابع همگرا می شوند . در خارج از این منطقه، چند جمله ای های درجه بالاتر تیلور تقریب بدتری برای تابع هستند.

خطایی که در تقریب یک تابع با چند جمله ای تیلور درجه n آن رخ می دهد، باقی مانده یا باقیمانده نامیده می شود و با تابع Rn ( x ) نشان داده می شود . از قضیه تیلور می توان برای به دست آوردن حدی در اندازه باقیمانده استفاده کرد .

به طور کلی، سری های تیلور به هیچ وجه نیازی به همگرایی ندارند . و در واقع مجموعه توابع با سری تیلور همگرا مجموعه ای ناچیز در فضای فریشه از توابع هموار است . و حتی اگر سری تیلور یک تابع f همگرا شود، نیازی نیست حد آن به طور کلی برابر با مقدار تابع f  ( x ) باشد . به عنوان مثال، تابع

{\displaystyle f(x)={\begin{cases}e^{-1/x^{2}}&{\text{if }}x\neq 0\\[3mu]0&{\text{if } }x=0\end{موارد}}}

بی نهایت در x = 0 مشتق پذیر است و تمام مشتقات آن صفر است. در نتیجه، سری تیلور از f  ( x ) در حدود x = 0 به طور یکسان صفر است. با این حال، f  ( x ) تابع صفر نیست، بنابراین با سری تیلور آن در اطراف مبدا برابر نیست. بنابراین، f  ( x ) مثالی از یک تابع هموار غیر تحلیلی است .

در تجزیه و تحلیل حقیقی ، این مثال نشان می دهد که توابع بی نهایت مشتق پذیر f  ( x ) وجود دارند که سری های تیلور آنها با f  ( x ) برابر نیستند ، حتی اگر همگرا شوند. در مقابل، توابع هولومورفیک مورد مطالعه در تحلیل مختلط همیشه دارای یک سری تیلور همگرا هستند، و حتی سری تیلور از توابع مرومورفیک ، که ممکن است دارای تکینگی باشند، هرگز به مقداری متفاوت از خود تابع همگرا نمی شوند. با این حال، تابع مختلط e -1/ z2 وقتی z در امتداد محور فرضی به 0 نزدیک می شود به 0 نزدیک نمی شود ، بنابراین در صفحه مختلط پیوسته نیست و سری تیلور آن در 0 تعریف نشده است.

به طور کلی تر، هر دنباله ای از اعداد حقیقی یا مختلط می تواند به عنوان ضرایبی در سری تیلور از یک تابع بی نهایت متمایز تعریف شده بر روی خط حقیقی ظاهر شود که نتیجه لم بورل است . در نتیجه، شعاع همگرایی یک سری تیلور می تواند صفر باشد. حتی توابع بی‌نهایت مشتق پذیر روی خط حقیقی تعریف شده‌اند که سری تیلور در همه جا شعاع همگرایی 0 دارند. [9]

یک تابع را نمی توان به عنوان یک سری تیلور با محوریت تکینگی نوشت . در این موارد، اگر قدرت های منفی متغیر x را نیز مجاز بدانیم، اغلب می توان به یک بسط سری دست یافت . سری لران را ببینید . برای مثال، f  ( x ) = e −1/ x 2 را می توان به صورت سری لران نوشت.