نشانه گذاری دیراک

برای حل معادله الکترونیکی شرودینگر در رایانه، تبدیل همه چیز به جبر خطی بسیار راحت است. ما می توانیم توابع موج را $\Psi({\bf r})$ به صورت بردار نشان دهیم:

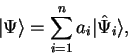$\begin{displaymath} \vert \Psi \rangle = \sum_{i=1}^{n} a_i \vert {\hat \Psi}_i \rangle , \end{displaymath}$

(5)

جایی که "بردار حالت" نامیده می شود، ضرایب بسط هستند (که ممکن است پیچیده باشند)، و بردارهای "مبنا" ثابت هستند. فضای برداری خطی مناسب (بی‌بعدی) برای چنین تجزیه‌هایی «فضای هیلبرت» نامیده می‌شود. $\vert \Psi \rangle$ $\vert {\hat \Psi}_i \rangle$

می توانیم مجموعه ضرایب را به صورت بردار ستونی بنویسیم، $\چپ\{ a_i \راست\}$

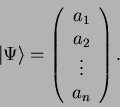$\begin{displaymath} \vert \Psi \rangle = \left( \begin{array}{c} a_1 \\ a_2 \\ \vdots \\ a_n \end{array} \right). \پایان{نمایشنامه}$

(6)

در نماد "براکت" (یا bra-ket) دیراک، ما "کت" می نامیم. در مورد الحاق این بردار چطور؟ این یک بردار ردیفی است که با علامت گذاری شده است ، که به آن "bra" (برای املای "bra-ket") می گویند. $\vert \Psi \rangle$ $\langle \Psi \vert$

$\begin{displaymath} \langle \Psi \vert = (a_1^* a_2^* \cdots a_n^*). \پایان{نمایشنامه}$

(7)

در جبر خطی، حاصل ضرب اسکالر بین دو بردار و فقط است $(\Psi_a,\Psi_b)$ $\Psi_a$ $\Psi_b$

$\begin{displaymath} (\Psi_a,\Psi_b) = (a_1^* a_2^* \cdots a_n^*) \left( \begin{a... ...\vdots \\ b_n \end{array} \ راست) = \sum_{i=1}^{n} a_i^* b_i، \end{displaymath}$

(8)

با فرض اینکه دو بردار در یک مجموعه مبنا نشان داده شده اند و بردارهای پایه متعامد هستند (در غیر این صورت، همپوشانی بین بردارهای پایه، به عنوان مثال، "متریک" باید لحاظ شود). مختصر مکانیکی کوانتومی برای محصول اسکالر فوق در نماد bra-ket درست است

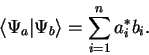$\begin{displaymath} \langle \Psi_a \vert \Psi_b \rangle = \sum_{i=1}^{n} a_i^* b_i. \پایان{نمایشنامه}$

(9)

اغلب، فرد فقط زیرنویس ها و در نماد دیراک را می نویسد، به طوری که ضرب نقطه ای بالا ممکن است به عنوان فقط نامیده شود . ترتیب بردارها و در حاصل ضرب نقطه ای در صورتی مهم است که بردارها بتوانند اعداد مختلط برای اجزای خود داشته باشند، زیرا . $\langle a \vert b \rangle$ $\Psi_a$ $\Psi_b$ $(\Psi_a, \Psi_b) = (\Psi_b, \Psi_a)^*$

حال فرض کنید که می خواهیم مجموعه پایه ما هر مقدار ممکن مختصات باشد . جدا از اینکه یک مجموعه پایه پیوسته (و نامتناهی) به ما می دهد، هیچ مشکل رسمی در این مورد وجود ندارد. سپس می توانیم یک حالت دلخواه را به صورت زیر نمایش دهیم:

$\begin{displaymath} \vert \Psi \rangle = \int_{-\infty}^{\infty} a_x \vert x \rangle dx. \پایان{نمایشنامه}$

(10)

ضرایب چیست ؟ معلوم می شود که این ضرایب به سادگی مقدار تابع موج در هر نقطه هستند . به این معنا که،

$\begin{displaymath} \vert \Psi \rangle = \int_{-\infty}^{\infty} \Psi(x) \vert x \rangle dx. \پایان{نمایشنامه}$

(11)

از آنجایی که هر دو مختصات متعامد در نظر گرفته می شوند (و همپوشانی آنها تابع دلتای دیراک می دهد)، حاصل ضرب اسکالر دو تابع حالت در فضای مختصات تبدیل می شود.

$\begin{displaymath} \langle \Psi_a \vert \Psi_b \rangle = \int_{-\infty}^{\infty} \Psi_a^*(x) \Psi_b(x) dx. \پایان{نمایشنامه}$

(12)

اکنون توجه خود را به نمایش ماتریسی عملگرها معطوف می کنیم. یک عملگر را $\hat{A}$ می توان با تأثیر آن بر بردارهای پایه مشخص کرد. عمل بردار $\hat{A}$ پایه مقداری بردار جدید به دست می‌دهد که تا زمانی که مجموعه پایه کاملی داشته باشیم، می‌توان آن را از نظر بردارهای پایه گسترش داد. $\vert \hat{\Psi}_j \rangle$ $\vert \Psi'_j \rangle$

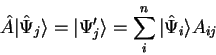$\begin{displaymath} \hat{A} \vert \hat{\Psi}_j \rangle = \vert \Psi'_j \rangle = \sum_i^{n} \vert \hat{\Psi}_i \rangle A_{ ij} \end{نمایشنامه}$

(13)

اگر تأثیر $\hat{A}$ بردارهای مبنا را بدانیم، $\hat{A}$ به دلیل خطی بودن $\hat{A}$ .

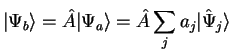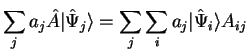$\displaystyle \vert \Psi_b \rangle = \hat{A} \vert \Psi_a \rangle = \hat{A} \sum_j a_j \vert \hat{\Psi}_j \rangle$	$\textstyle =$	$\displaystyle \sum_j a_j \hat{A} \vert \hat{\Psi}_j \rangle = \sum_j \sum_i a_j \vert \hat{\Psi}_i \rangle A_{ij}$	(14)
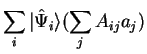	$\textstyle =$	$\displaystyle \sum_i \vert \hat{\Psi}_i \rangle ( \sum_j A_{ij} a_j )$

یا

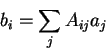$\begin{displaymath} b_i = \sum_j A_{ij} a_j \end{displaymath}$

(15)

این ممکن است به صورت نماد ماتریسی نوشته شود

$\begin{displaymath} \left( \begin{array}{c} b_1 \\ b_2 \\ \vdots \\ b_n \end{... ...n{array}{c} a_1 \\ a_2 \\\ vdots \\ a_n \end{array} \right) \end{displaymath}$

(16)

می توانیم ضرایب را $A_{ij}$ با گرفتن حاصل ضرب داخلی هر دو طرف معادله 13 به دست آوریم $\hat{\Psi}_i$ .

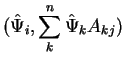$\displaystyle (\hat{\Psi}_i, \hat{A} \hat{\Psi}_j)$	$\textstyle =$	$\displaystyle (\hat{\Psi}_i، \sum_k^{n} \hat{\Psi}_k A_{kj})$	(17)
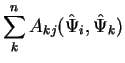	$\textstyle =$	$\displaystyle \sum_k^{n} A_{kj} (\hat{\Psi}_i، \hat{\Psi}_k)$
	$\textstyle =$	$\displaystyle A_{ij}$

از آنجایی که به دلیل متعارف بودن پایه. در نماد bra-ket، ممکن است بنویسیم $(\hat{\Psi}_i، \hat{\Psi}_k) = \delta_{ik}$

$\begin{displaymath} A_{ij} = \langle i \vert \hat{A} \vert j \rangle \end{displaymath}$

(18)

کجا و دو بردار پایه را نشان می دهد. اگر متوجه شویم که فقط یک بردار دیگر است، این استفاده از نماد bra-ket با استفاده قبلی آن سازگار است . $\hat{A} \vert j \rangle$ $\vert j' \rangle$

به راحتی می توان نشان داد که برای یک عملگر خطی $\hat{A}$ ، حاصلضرب داخلی برای دو بردار کلی (نه لزوما بردارهای پایه) و با $(\Psi_a، \hat{A} \Psi_b)$ $\Psi_a$ $\Psi_b$

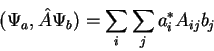$\begin{displaymath} (\Psi_a, \hat{A} \Psi_b) = \sum_i \sum_j a_i^{*} A_{ij} b_j \end{displaymath}$

(19)

یا در نماد ماتریسی

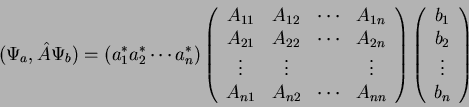$\begin{displaymath} (\Psi_a, \hat{A} \Psi_b) = \left( a_1^{*} a_2^{*} \cdots a_n... ...n{array}{c} b_1 \\ b_2 \\ \vdots \\ b_n \end{array} \right) \end{displaymath}$

(20)

با قیاس با معادله ( 12 )، ممکن است به طور کلی این ضرب درونی را به شکل بنویسیم

$\begin{displaymath} (\Psi_a, \hat{A} \Psi_b) = \langle a \vert \hat{A} \vert b \rangle = \int \Psi_a^{*}(x) \hat{A} \Psi_b(x) dx \end{displaymath}$

(21)

قبلاً اشاره کردیم که یا . بنابراین ما می توانیم آن را نیز ببینیم $(\Psi_a, \Psi_b) = (\Psi_b, \Psi_a)^{*}$ $\langle a \vert b \rangle = \langle b \vert a \rangle^{*}$

$\begin{displaymath} (\Psi_a, \hat{A} \Psi_b) = (\hat{A} \Psi_b, \Psi_a)^{*} \end{displaymath}$

(22)

اکنون الحاق یک عملگر را تعریف می کنیم $\hat{A}$ که با علامت آن عملگر خطی برای آن مشخص می شود $\hat{A}^{\dagger}$

$\begin{displaymath} (\Psi_a, \hat{A} \Psi_b) = (\hat{A}^{\dagger} \Psi_a, \Psi_b) \end{displaymath}$

(23)

یعنی ما می‌توانیم کاری کنیم که یک عملگر به سمت عقب در فضای «bra» عمل کند، اگر آن را مجاور بدانیم. با این تعریف، ما می توانیم بیشتر ببینیم که

$\begin{displaymath} (\Psi_a, \hat{A} \Psi_b) = (\hat{A} \Psi_b, \Psi_a)^{*} = (... ...A}^{\Dagger} \ Psi_a)^{*} = (\hat{A}^{\dagger} \Psi_a, \Psi_b) \end{displaymath}$

(24)

یا در نماد bra-ket،

$\begin{displaymath} \langle a \vert \hat{A} \vert b \rangle = \langle \hat{A} b ... ... a \rangle ^{*} = \langle \hat{A} ^{\ dagger} a \vert b \rangle \end{displaymath}$

(25)

اگر و را انتخاب کنیم (یعنی اگر دو بردار پایه را انتخاب کنیم)، آنگاه به دست می آوریم $\Psi_a = \hat{\Psi}_i$ $\Psi_b = \hat{\Psi}_j$

$\displaystyle (\hat{A} \hat{\Psi}_i, \hat{\Psi}_j)$	$\textstyle =$	$\displaystyle (\hat{\Psi}_i, \hat{A}^{\dagger} \hat{\Psi}_j)$	(26)
$\displaystyle (\hat{\Psi}_j, \hat{A} \hat{\Psi}_i)^{*}$	$\textstyle =$	$\displaystyle (\hat{\Psi}_i, \hat{A}^{\dagger} \hat{\Psi}_j)$
$\displaystyle A_{ji}^{*}$	$\textstyle =$	$\displaystyle A^{\dagger}_{ij}$

اما این دقیقاً شرط عناصر یک ماتریس و الحاق آن است! بنابراین ضمیمه نمایش ماتریسی از $\hat{A}$ همان نمایش ماتریسی است . $\hat{A}^{\dagger}$

این تطابق بین عملگرها و نمایش‌های ماتریسی آنها بسیار زیاد است، اگرچه البته نمایش ماتریس خاص به انتخاب مبنا بستگی دارد. به عنوان مثال، از جبر خطی می دانیم که اگر یک ماتریس و الحاق آن یکسان باشند، ماتریس هرمیتین نامیده می شود. همین امر در مورد اپراتورها نیز صادق است. اگر

$\begin{displaymath} \hat{A} = \hat{A}^{\dagger} \end{displaymath}$

(27)

سپس $\hat{A}$ یک عملگر هرمیتی است، و تمام خصوصیات ویژه عملگرهای هرمیتی برای $\hat{A}$ یا نمایش ماتریسی آن اعمال می شود.

http://vergil.chemistry.gatech.edu/notes/intro_estruc/node5.html

+ نوشته شده در پنجشنبه دوم آذر ۱۴۰۲ ساعت 16:18 توسط علی رضا نقش نیلچی |

ریاضیات

آموزش ریاضی

نشانه گذاری دیراک

پیوندهای روزانه

نوشته‌های پیشین

آرشیو موضوعی

پیوندها

آمارگیر وبلاگ

کد پربازدیدترین