مقادیر انتظاری مقادیر فیزیکی
ارزش های انتظاری
عملگرها به ما این امکان را می دهند که مقدار انتظاری برخی از کمیت های فیزیک را با توجه به تابع موج محاسبه کنیم. اگر یک ذره در حالت باشد 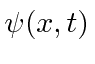 ، روش معمولی برای محاسبه مقدار انتظاری
، روش معمولی برای محاسبه مقدار انتظاری 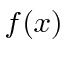 است
است
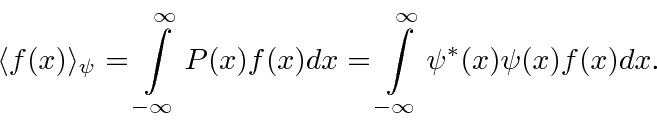
میتوانیم 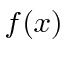 قبل از
قبل از ![]() پیشبینی استفاده از عملگرهای خطی، بین این دو حرکت کنیم.
پیشبینی استفاده از عملگرهای خطی، بین این دو حرکت کنیم.
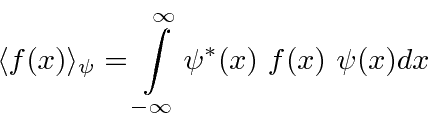
اگر متغیری که میخواهیم مقدار انتظاری (مانند ![]() ) را محاسبه کنیم تابع سادهای نیست
) را محاسبه کنیم تابع سادهای نیست ![]() ، اجازه دهید عملگر آن عمل کند
، اجازه دهید عملگر آن عمل کند 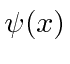 . ارزش انتظاری از
. ارزش انتظاری از ![]() در حالت
در حالت ![]() است
است
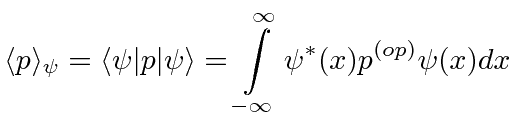 |
نمادبراکت دیراک که در بالا نشان داده شده است، روشی مناسب برای نشان دادن مقدار انتظاری یک متغیر با توجه به حالتی است.
* مثال: یک ذره در حالت است . ارزش انتظاری چیست ؟ 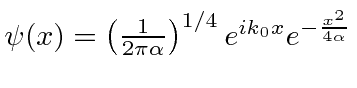
![]() *
*
برای هر کمیت فیزیکی ![]() ، مقدار انتظاری
، مقدار انتظاری ![]() در حالت دلخواه
در حالت دلخواه![]() برابر است
برابر است
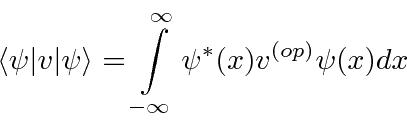
مقادیر انتظاری مقادیر فیزیکی باید واقعی باشد .
Gasiorowicz فصل 3
گریفیث فصل 1
کوهن تنودجی و همکاران. فصل
https://quantummechanics.ucsd.edu/ph130a/130_notes/node107.html
 در این وبلاگ به ریاضیات و کاربردهای آن و تحقیقات در آنها پرداخته می شود. مطالب در این وبلاگ ترجمه سطحی و اولیه است و کامل نیست.در صورتی سوال یا نظری در زمینه ریاضیات دارید مطرح نمایید .در صورت امکان به آن می پردازم. من دوست دارم برای یافتن پاسخ به سوالات و حل پروژه های علمی با دیگران همکاری نمایم.در صورتی که شما هم بامن هم عقیده هستید با من تماس بگیرید.
در این وبلاگ به ریاضیات و کاربردهای آن و تحقیقات در آنها پرداخته می شود. مطالب در این وبلاگ ترجمه سطحی و اولیه است و کامل نیست.در صورتی سوال یا نظری در زمینه ریاضیات دارید مطرح نمایید .در صورت امکان به آن می پردازم. من دوست دارم برای یافتن پاسخ به سوالات و حل پروژه های علمی با دیگران همکاری نمایم.در صورتی که شما هم بامن هم عقیده هستید با من تماس بگیرید.