8- تکانه زاویه ای

عدم قطعیت [ ویرایش ]

در تعریف $\mathbf {L} =\mathbf {r} \times \mathbf {p}$ شش عملگر درگیر هستند: عملگرهای موقعیت $r_{x}$ ، $r_{y}$ ، $r_{z}$ و عملگرهای تکانه $p_{x}$ ، $p_{y}$ ، $p_{z}$ . با این حال، اصل عدم قطعیت هایزنبرگ به ما می‌گوید که امکان ندارد هر شش این کمیت به طور همزمان با دقت دلخواه شناخته شوند. بنابراین، محدودیت هایی برای دانستن یا اندازه گیری تکانه زاویه ای یک ذره وجود دارد. به نظر می رسد که بهترین کاری که می توان انجام داد این است که هم قدر بردار تکانه زاویه ای و هم جزء آن را در امتداد یک محور اندازه گیری کنیم.

عدم قطعیت ارتباط نزدیکی با این واقعیت دارد که اجزای مختلف یک اپراتور تکانه زاویه ای جابجا نمی شوند $L_{x}L_{y}\neq L_{y}L_{x}$ . (برای روابط کموتاسیون دقیق ، عملگر حرکت زاویه ای را ببینید .)

تکانه زاویه ای کل به عنوان مولد چرخش [ ویرایش ]

همانطور که در بالا ذکر شد، تکانه زاویه ای مداری L به صورت زیر در مکانیک کلاسیک تعریف می شود: $\mathbf {L} =\mathbf {r} \times \mathbf {p}$ ، اما تکانه زاویه ای کل J به روشی متفاوت و اساسی تر تعریف می شود: J به عنوان "مولد چرخش" تعریف می شود. [40] به طور خاص، J به گونه ای تعریف می شود که عملگر

$R({\hat {n}},\phi )\equiv \exp \left(-{\frac {i}{\hbar }}\phi \,\mathbf {J} \cdot {\hat { \mathbf {n} }}\راست)$

عملگر چرخشی است که هر سیستمی را می گیرد و آن را برحسب زاویه می چرخاند $\phi$ در مورد محور ${\hat {\mathbf {n} }}$ . («exp» در فرمول به عملگر نمایی اشاره دارد ) برای بیان این موضوع، فضای هیلبرت کوانتومی ما هر چه باشد، انتظار داریم که گروه چرخشی SO(3) بر روی آن عمل کند. سپس یک عمل مرتبط از جبر دروغ so(3) از SO(3) وجود دارد. عملگرهایی که عمل so(3) را در فضای هیلبرت ما توصیف می کنند، عملگرهای تکانه زاویه ای (کل) هستند.

رابطه بین عملگر تکانه زاویه ای و عملگرهای چرخش مانند رابطه بین جبرهای Lie و گروه های Lie در ریاضیات است. رابطه نزدیک بین تکانه زاویه ای و چرخش ها در قضیه نوتر منعکس شده است که ثابت می کند هر زمان که قوانین فیزیک از نظر چرخشی ثابت باشند، تکانه زاویه ای حفظ می شود.

تکانه زاویه ای در الکترودینامیک [ ویرایش ]

همچنین ببینید: تکانه (ذره در میدان)

هنگام توصیف حرکت یک ذره باردار در یک میدان الکترومغناطیسی ، تکانه متعارف P (که از لاگرانژ برای این سیستم به دست می‌آید) گیج ثابت نیست . در نتیجه، تکانه زاویه ای متعارف L = r × P نیز ثابت نیست. در عوض، تکانه ای که فیزیکی است، به اصطلاح تکانه جنبشی (در سراسر این مقاله استفاده می شود)، (به واحد SI ) است.

$\mathbf {p} =m\mathbf {v} =\mathbf {P} -e\mathbf {A}$

که e بار الکتریکی ذره و A پتانسیل بردار مغناطیسی میدان الکترومغناطیسی است . تکانه زاویه ای گیج ثابت، که تکانه زاویه ای جنبشی است ، توسط

$\mathbf {K} =\mathbf {r} \times (\mathbf {P} -e\mathbf {A} )$

تعامل با مکانیک کوانتومی در مقاله روابط کموتاسیون متعارف بیشتر مورد بحث قرار گرفته است .

تکانه زاویه ای در اپتیک [ ویرایش ]

در الکترودینامیک ماکسول کلاسیک، بردار Poynting چگالی تکانه خطی میدان الکترومغناطیسی است. [41]

$\mathbf {S} (\mathbf {r} ,t)=\epsilon _{0}c^{2}\mathbf {E} (\mathbf {r} ,t)\times \mathbf {B} (\mathbf {r} ,t).$

بردار چگالی تکانه زاویه ای $\mathbf {L} (\mathbf {r} ,t)$ توسط یک ضرب برداری مانند مکانیک کلاسیک داده می شود: [42]

${\displaystyle \mathbf {l} (\mathbf {r} ,t)=\epsilon _{0}\mu _{0}\mathbf {r} \times \mathbf {S} (\mathbf {r} ,t )$

اتحاد های فوق به صورت محلی معتبر هستند ، یعنی در هر نقطه فاصله $\mathbf {r}$ در یک لحظه معین $تی$ .

حرکت زاویه ای در طبیعت و کیهان [ ویرایش ]

طوفان های استوایی و سایر پدیده های آب و هوایی مرتبط با حفظ تکانه زاویه ای به منظور توضیح دینامیک همراه هستند. بادها به آرامی در اطراف سیستم های کم فشار می چرخند که عمدتاً به دلیل اثر کوریولیس است . اگر فشار پایین تشدید شود و هوای به آرامی در گردش به سمت مرکز کشیده شود، مولکول ها باید سرعت خود را افزایش دهند تا تکانه زاویه ای را حفظ کنند. با رسیدن به مرکز، سرعت ها مخرب می شوند. [43]

یوهانس کپلر قوانین حرکت سیارات را بدون آگاهی از بقای تکانه تعیین کرد. با این حال، اندکی پس از کشف او، اشتقاق آنها از بقای تکانه زاویه ای مشخص شد. سیارات هر چه بیشتر در مدارهای بیضی شکل خود قرار بگیرند، آهسته تر حرکت می کنند، که به طور شهودی با این واقعیت توضیح داده می شود که تکانه زاویه ای مداری متناسب با شعاع مدار است. از آنجایی که جرم تغییر نمی کند و تکانه زاویه ای حفظ می شود، سرعت کاهش می یابد.

شتاب جزر و مدی اثر نیروهای جزر و مدی بین یک ماهواره طبیعی در حال گردش (به عنوان مثال ماه ) و سیاره اولیه ای است که به دور آن می چرخد (مثلا زمین). گشتاور گرانشی بین ماه و برآمدگی جزر و مدی زمین باعث می شود که ماه دائماً به مداری کمی بالاتر رفته و زمین در چرخش خود کاهش یابد. زمین حرکت زاویه ای خود را از دست می دهد که به ماه منتقل می شود به طوری که تکانه زاویه ای کلی حفظ می شود.

حرکت زاویه ای در مهندسی و فناوری [ ویرایش ]

ویدئو: ابزار تمرین ژیروسکوپی کاربرد حفظ تکانه زاویه ای برای تقویت عضلات است. جرمی که به سرعت حول محور خود در یک وسیله توپی شکل می چرخد، تکانه زاویه ای را مشخص می کند. هنگامی که فردی که تمرین می کند توپ را کج می کند، نیرویی ایجاد می شود که حتی در صورت واکنش خاص توسط کاربر، سرعت چرخش را افزایش می دهد.

نمونه هایی از استفاده از بقای حرکت زاویه ای برای مزیت عملی فراوان است. در موتورهایی مانند موتورهای بخار یا موتورهای احتراق داخلی ، یک چرخ طیار برای تبدیل موثر حرکت جانبی پیستون ها به حرکت چرخشی مورد نیاز است.

سیستم های ناوبری اینرسی به صراحت از این واقعیت استفاده می کنند که تکانه زاویه ای با توجه به قاب اینرسی فضا حفظ می شود. ناوبری اینرسی همان چیزی است که سفرهای زیردریایی را در زیر کلاهک یخی قطبی امکان پذیر می کند، اما برای همه اشکال ناوبری مدرن نیز بسیار مهم است.

گلوله‌های تفنگدار از پایداری حاصل از حفظ تکانه زاویه‌ای استفاده می‌کنند تا در مسیر حرکت خود صادق‌تر باشند. اختراع سلاح های گرم و توپ به کاربران آنها مزیت استراتژیک قابل توجهی در نبرد داد و بنابراین نقطه عطف تکنولوژیک در تاریخ بود.

تاریخچه [ ویرایش ]

اسحاق نیوتن در پرینسیپیا در مثالهای خود از قانون اول حرکت به تکانه زاویه ای اشاره کرد .

قسمت بالایی که به دلیل انسجام آنها دائماً از حرکات مستطیلی جدا می شود، چرخش خود را متوقف نمی کند، مگر اینکه توسط هوا عقب افتاده باشد. اجسام بزرگتر سیارات و دنباله دارها که در فضاهای آزاد بیشتر با مقاومت کمتری روبرو می شوند، حرکات خود را هم به صورت پیشرونده و هم دایره ای برای مدت طولانی تری حفظ می کنند. [44]

او بیشتر به بررسی تکانه زاویه ای به طور مستقیم در Principia پرداخت و گفت:

از این نوع بازتاب ها نیز گاهی اوقات حرکات دایره ای اجسام در حول مرکز خود به وجود می آید. اما اینها مواردی است که در ادامه به آنها توجه نمی کنم. و نشان دادن هر چیز خاصی که به این موضوع مربوط می شود بسیار خسته کننده خواهد بود. [45]

با این حال، اثبات هندسی او از قانون مساحت ها نمونه برجسته ای از نبوغ نیوتن است و به طور غیرمستقیم پایستگی تکانه زاویه ای را در مورد نیروی مرکزی ثابت می کند .

قانون مناطق [ ویرایش ]

مقاله‌های اصلی: مسئله نیروی مرکزی کلاسیک و سرعت منطقه‌ای

اشتقاق نیوتن [ ویرایش ]

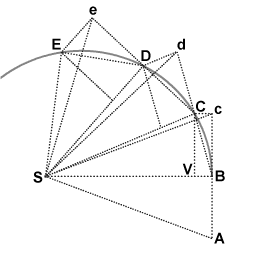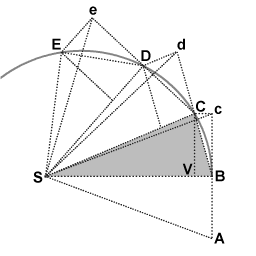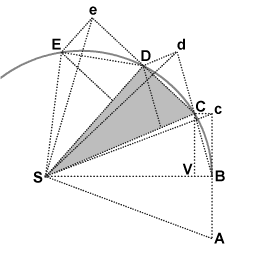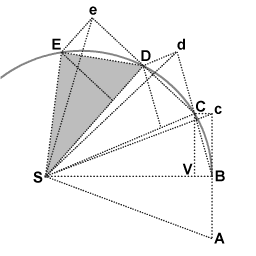
اشتقاق نیوتن از قانون مساحت با استفاده از ابزارهای هندسی

همانطور که یک سیاره به دور خورشید می چرخد ، خط بین خورشید و سیاره در فواصل زمانی مساوی مناطق مساوی را رد می کند. این موضوع از زمانی که کپلر قانون دوم خود را در مورد حرکت سیارات توضیح داد شناخته شده بود . نیوتن یک اثبات هندسی منحصر به فرد به دست آورد و در ادامه نشان داد که نیروی جاذبه گرانش خورشید علت همه قوانین کپلر است.

در اولین بازه زمانی، یک جسم از نقطه A به نقطه B در حرکت است . بدون مزاحمت، در بازه دوم به نقطه c ادامه خواهد داد . هنگامی که جسم به B می رسد ، یک ضربه به سمت نقطه S دریافت می کند . ضربه یک سرعت اضافه کوچک به سمت S به آن می دهد، به طوری که اگر این تنها سرعت آن بود، در بازه دوم از B به V حرکت می کرد . با قوانین ترکیب سرعت ، این دو سرعت جمع می شوند و نقطه C با ساخت متوازی الاضلاع BcCV پیدا می شود.. بنابراین مسیر جسم توسط ضربه منحرف می شود به طوری که در انتهای بازه دوم به نقطه C می رسد. از آنجایی که مثلث های SBc و SBC دارای پایه SB یکسان و ارتفاع Bc یا VC یکسان هستند ، مساحت یکسانی دارند. از نظر تقارن، مثلث SBc نیز مساحت مثلث SAB را دارد ، بنابراین جسم در زمان‌های مساوی ، مساحت‌های SAB و SBC را از بین برده است.

در نقطه C ، جسم یک تکانه دیگر به سمت S دریافت می کند ، و دوباره مسیر خود را در بازه سوم از d به D منحرف می کند . بنابراین تا E و فراتر از آن ادامه می‌یابد، مثلث‌های SAB ، SBc ، SBC ، SCd ، SCD ، SDe ، SDE همگی مساحت یکسانی دارند. با اجازه دادن به فواصل زمانی کوچکتر، مسیر ABCDE به طور نامحدود به یک منحنی پیوسته نزدیک می شود.

توجه داشته باشید که چون این اشتقاق هندسی است و هیچ نیروی خاصی اعمال نمی شود، قانون کلی تری نسبت به قانون دوم حرکت سیاره کپلر ثابت می کند. این نشان می دهد که قانون مساحت ها برای هر نیروی مرکزی، جاذبه یا دافعه، پیوسته یا ناپیوسته یا صفر اعمال می شود.

پایستگی تکانه زاویه ای در قانون مساحت ها [ ویرایش ]

تناسب تکانه زاویه ای با ناحیه ای که توسط یک جسم متحرک خارج می شود را می توان با درک اینکه پایه های مثلث ها، یعنی خطوط S به جسم، معادل شعاع r هستند و ارتفاعات مثلث ها متناسب با مولفه عمود بر سرعت v ⊥ هستند . بنابراین، اگر مساحت جاروب شده در واحد زمان ثابت باشد، با فرمول مساحت مثلثی1/2(پایه)(ارتفاع) ، حاصلضرب (پایه)(ارتفاع) و در نتیجه حاصلضرب rv ⊥ ثابت است: اگر r و طول پایه کاهش یابد، v ⊥ و ارتفاع باید به نسبت افزایش یابد. جرم ثابت است، بنابراین تکانه زاویه ای rmv ⊥ با این تبادل فاصله و سرعت حفظ می شود.

در مورد مثلث SBC مساحت برابر است با1/2( SB ) ( VC ). هر جا C در نهایت به دلیل ضربه اعمال شده در B قرار گیرد ، حاصلضرب ( SB )( VC ) و بنابراین rmv ⊥ ثابت می ماند. به همین ترتیب برای هر یک از مثلث ها.

بعد از نیوتن [ ویرایش ]

لئونارد اویلر ، دانیل برنولی و پاتریک دارسی همگی تکانه زاویه‌ای را بر حسب بقای سرعت منطقه‌ای ، نتیجه تحلیل قانون دوم کپلر در مورد حرکت سیاره‌ها، درک کردند. بعید است که آنها متوجه پیامدهای آن برای ماده چرخان معمولی شده باشند. [46]

در سال 1736 اویلر، مانند نیوتن، برخی از معادلات تکانه زاویه ای را در مکانیکای خود بدون توسعه بیشتر لمس کرد. [47]

برنولی در نامه ای در سال 1744 از "لحظه حرکت چرخشی" نوشت که احتمالاً اولین تصور از تکانه زاویه ای است که اکنون آن را درک می کنیم. [48]

در سال 1799، پیر سیمون لاپلاس برای اولین بار متوجه شد که یک صفحه ثابت با چرخش مرتبط است - صفحه ثابت او .

لویی پوانسو در سال 1803 شروع به نمایش چرخش به عنوان یک پاره خط عمود بر چرخش کرد و در مورد "حفظ لحظه ها" توضیح داد.

در سال 1852 لئون فوکو از یک ژیروسکوپ در آزمایشی برای نمایش چرخش زمین استفاده کرد.

کتابچه راهنمای مکانیک کاربردی ویلیام جی ام رانکین در سال 1858 ، تکانه زاویه ای را برای اولین بار به معنای امروزی تعریف کرد:

... خطی که طول آن متناسب با بزرگی تکانه زاویه ای باشد و جهت آن عمود بر صفحه حرکت جسم و نقطه ثابت باشد و به گونه ای که وقتی حرکت جسم را از زاویه نگاه کنیم. انتهای خط، شعاع بردار بدن به نظر می رسد چرخش سمت راست دارد.

در نسخه 1872 همان کتاب، رانکین بیان کرد که "اصطلاح حرکت زاویه ای توسط آقای هیوارد معرفی شد" [49] احتمالاً به مقاله RB Hayward در مورد روش مستقیم تخمین سرعت ها، شتاب ها و تمام کمیت های مشابه با احترام اشاره می کند. به Axes قابل جابجایی به هر شکلی در Space with Applications، [50] که در سال 1856 معرفی شد و در سال 1864 منتشر شد. Rankine اشتباه بود، زیرا انتشارات متعددی این اصطلاح را در اواخر قرن 18 تا اوایل قرن 19 نشان می‌دهند. [51] با این حال، ظاهراً مقاله هیوارد اولین استفاده از این اصطلاح و مفهومی بود که توسط بسیاری از کشورهای انگلیسی زبان دیده می شد. قبل از این، تکانه زاویه ای به طور معمول در انگلیسی به عنوان "تکانه چرخش" نامیده می شد.[52]

همچنین ببینید [ ویرایش ]

منبع

https://en.wikipedia.org/wiki/Angular_momentum

+ نوشته شده در دوشنبه یکم خرداد ۱۴۰۲ ساعت 20:17 توسط علی رضا نقش نیلچی |

ریاضیات

آموزش ریاضی