چهار تکانه [ ویرایش ]

به دلیل رابطه نزدیک بین جرم و انرژی، چهار تکانه (که 4 تکانه نیز نامیده می شود) انرژی- تکانه 4-بردار نیز نامیده می شود. با استفاده از حروف بزرگ P برای نشان دادن تکانه چهار و حروف کوچک p برای نشان دادن تکانه فضایی، چهار تکانه ممکن است به صورت نوشته شود.

{\displaystyle P\equiv (E/c,{\vec {p}})=(E/c,p_{x},p_{y},p_{z})}یا به طور متناوب،

{\displaystyle P\equiv (E,{\vec {p}})=(E,p_{x},p_{y},p_{z})}با استفاده از کنوانسیون که{\displaystyle c=1.}[41] : 129-130، 180 

قوانین حفاظت [ ویرایش ]

مقاله اصلی: قانون حفاظت

در فیزیک، قوانین حفاظت بیان می کنند که برخی از ویژگی های خاص قابل اندازه گیری یک سیستم فیزیکی جدا شده با تکامل سیستم در طول زمان تغییر نمی کند. در سال 1915، امی نوتر کشف کرد که زیربنای هر قانون حفاظتی، تقارن اساسی طبیعت است. [46] این واقعیت که فرآیندهای فیزیکی اهمیتی نمی‌دهند که در کجا در فضا اتفاق می‌افتند ( تقارن ترجمه فضایی ) باعث بقای تکانه می‌شود ، این واقعیت که چنین فرآیندهایی به زمان وقوع اهمیتی نمی‌دهند ( تقارن ترجمه زمانی ) بقای انرژی را به همراه دارد.، و غیره. در این بخش، دیدگاه‌های نیوتنی در مورد بقای جرم، تکانه و انرژی را از دیدگاه نسبیتی بررسی می‌کنیم.

حرکت کل [ ویرایش ]

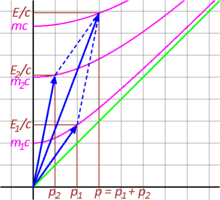
شکل 3-10. حفظ نسبیتی حرکت

برای درک اینکه چگونه دیدگاه نیوتنی در مورد بقای تکانه باید در یک زمینه نسبیتی اصلاح شود، مشکل دو جسم در حال برخورد محدود به یک بعد واحد را بررسی می کنیم.

در مکانیک نیوتنی، دو حالت افراطی از این مسئله را می‌توان متمایز کرد که ریاضیات با حداقل پیچیدگی را به دست می‌دهد:

(1) این دو بدن در یک برخورد کاملاً الاستیک از یکدیگر باز می گردند.

(2) دو جسم به هم می چسبند و به صورت یک ذره به حرکت خود ادامه می دهند. این مورد دوم مورد برخورد کاملا غیر ارتجاعی است.

برای هر دو حالت (1) و (2)، تکانه، جرم و انرژی کل حفظ می شود. با این حال، انرژی جنبشی در موارد برخورد غیر کشسان حفظ نمی شود. بخش معینی از انرژی جنبشی اولیه به گرما تبدیل می شود.

در حالت (2) دو جرم با تکانه{\displaystyle {\boldsymbol {p}}_{\boldsymbol {1}}=m_{1}{\boldsymbol {v}}_{\boldsymbol {1}}} و{\displaystyle {\boldsymbol {p}}_{\boldsymbol {2}}=m_{2}{\boldsymbol {v}}_{\boldsymbol {2}}}برخورد می کنند تا یک ذره با جرم حفظ شده تولید کنند{\displaystyle m=m_{1}+m_{2}}حرکت در مرکز سرعت جرم سیستم اصلی،{\displaystyle {\boldsymbol {v_{cm}}}=\left(m_{1}{\boldsymbol {v_{1}}}+m_{2}{\boldsymbol {v_{2}}}\راست)/ \left(m_{1}+m_{2}\right)}. کل حرکت{\displaystyle {\boldsymbol {p=p_{1}+p_{2}}}}حفظ شده است.

شکل 3-10 برخورد غیرکشسان دو ذره را از منظر نسبیتی نشان می دهد. اجزای زمان{\displaystyle E_{1}/c}و{\displaystyle E_{2}/c}کل E/c بردار حاصل را جمع کنید، به این معنی که انرژی حفظ می شود. به همین ترتیب، اجزای فضا{\displaystyle {\boldsymbol {p_{1}}}}و{\displaystyle {\boldsymbol {p_{2}}}}جمع کنید تا p بردار حاصل را تشکیل دهید. همانطور که انتظار می رود، چهار تکانه یک کمیت حفظ شده است. با این حال، جرم ثابت ذره ذره‌ای که با نقطه‌ای که هذلولی ثابت تکانه کل محور انرژی را قطع می‌کند، به دست می‌آید، با مجموع جرم‌های ثابت ذرات منفرد که با هم برخورد کرده‌اند، برابر نیست. در واقع، بزرگتر از مجموع توده های فردی است:{\displaystyle m>m_{1}+m_{2}}. [39] : 94-97 

با نگاهی به وقایع این سناریو به ترتیب معکوس، می بینیم که عدم پایستگی جرم یک اتفاق رایج است: وقتی یک ذره بنیادی ناپایدار به طور خود به خود به دو ذره سبک تر تجزیه می شود، انرژی کل حفظ می شود، اما جرم اینطور نیست. بخشی از جرم به انرژی جنبشی تبدیل می شود. [41] : 134-138 

انتخاب فریم های مرجع [ ویرایش ]

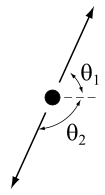
شکل 3-11.
(بالا) قاب آزمایشگاه .
(راست) مرکز قاب مومنتوم .

آزادی انتخاب هر فریمی که در آن تجزیه و تحلیل انجام شود به ما امکان می دهد فریمی را انتخاب کنیم که بسیار راحت باشد. برای تجزیه و تحلیل مسائل تکانه و انرژی، راحت‌ترین قاب معمولاً «قاب مرکز تکانه » است (که قاب تکانه صفر یا قاب COM نیز نامیده می‌شود). این قاب است که در آن جزء فضایی تکانه کل سیستم صفر است. شکل 3-11 تجزیه یک ذره با سرعت بالا را به دو ذره دختر نشان می دهد. در قاب آزمایشگاه، ذرات دختر ترجیحاً در جهتی در امتداد مسیر ذره اصلی منتشر می شوند. با این حال، در قاب COM، دو ذره دختر در جهت مخالف ساطع می شوند، اگرچه جرم و بزرگی سرعت آنها معمولاً یکسان نیست.

بقای انرژی و تکانه [ ویرایش ]

در یک تحلیل نیوتنی از ذرات برهم کنش، تبدیل بین فریم ها ساده است، زیرا تنها چیزی که لازم است اعمال تبدیل گالیله برای همه سرعت ها است. از آنجا که{\displaystyle v'=vu}، حرکت{\displaystyle p'=p-mu}. اگر تکانه کل یک سیستم متقابل ذرات در یک قاب حفظ شود، به همین ترتیب مشاهده خواهد شد که در هر قاب دیگری حفظ شده است. [41] : 241-245 

حفظ تکانه در قاب COM به این نیاز است که قبل و بعد از برخورد p = 0 . در تحلیل نیوتنی، حفظ جرم حکم می کند{\displaystyle m=m_{1}+m_{2}}. در سناریوهای ساده و تک بعدی که در نظر گرفته‌ایم، تنها یک محدودیت اضافی قبل از تعیین لحظه خروجی ذرات ضروری است - یک شرط انرژی. در حالت یک بعدی یک برخورد کاملاً الاستیک و بدون از دست دادن انرژی جنبشی، سرعت خروجی ذرات برگشتی در قاب COM دقیقاً برابر و مخالف سرعت ورودی آنها خواهد بود. در صورت یک برخورد کاملا غیر کشسان با از دست دادن کل انرژی جنبشی، سرعت خروجی ذرات برگشتی صفر خواهد بود. [41] : 241-245 

گشتاور نیوتنی، محاسبه شده به عنوانp = mv، تحت تحول لورنتسی نمی توانند به درستی رفتار کنند. تبدیل خطی سرعت ها{\displaystyle v'=vu}بسیار غیرخطی جایگزین می شود {\displaystyle v^{\prime }=(vu){\Big/}\left(1-{\frac {vu}{c^{2}}}\right)}به طوری که محاسباتی که بقای تکانه را در یک فریم نشان می دهد در فریم های دیگر نامعتبر خواهد بود. انیشتین یا مجبور بود از حفظ تکانه دست بکشد یا تعریف تکانه را تغییر دهد. این گزینه دوم همان چیزی بود که او انتخاب کرد. [39] : 104 

شکل 3-12 الف. نمودار انرژی – تکانه برای فروپاشی یک پیون باردار.

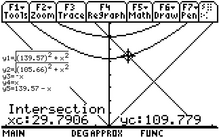
شکل 3-12b. تجزیه و تحلیل نموداری ماشین حساب واپاشی پیون باردار.

قانون بقای نسبیتی برای انرژی و تکانه جایگزین سه قانون کلاسیک بقای انرژی، تکانه و جرم می شود. جرم دیگر به طور مستقل حفظ نمی شود، زیرا در کل انرژی نسبیتی قرار گرفته است. این باعث می‌شود که بقای نسبیتی انرژی مفهومی ساده‌تر از مکانیک غیرنسبیتی باشد، زیرا انرژی کل بدون هیچ شرطی حفظ می‌شود. انرژی جنبشی تبدیل شده به گرما یا انرژی پتانسیل داخلی با افزایش جرم خود را نشان می دهد. [41] : 127 

مثال: به دلیل هم ارزی جرم و انرژی، جرم ذرات بنیادی معمولاً در واحدهای انرژی بیان می‌شود که 1 MeV = 106 الکترون ولت است. یک پیون باردار ذره ای با جرم 139.57 مگا الکترون ولت (تقریباً 273 برابر جرم الکترون) است. ناپایدار است و به یک میون با جرم 105.66 مگا الکترون ولت (تقریباً 207 برابر جرم الکترون) و یک پادنوترینو که جرمی تقریباً ناچیز دارد تجزیه می شود. تفاوت بین جرم پیون و جرم میون 33.91 مگا ولت است.


π-
→
μ-
+
ν
μ

شکل 3-12a نمودار انرژی – تکانه را برای این واکنش فروپاشی در قاب استراحت پایون نشان می دهد. به دلیل جرم ناچیزش، یک نوترینو با سرعت بسیار نزدیک به نور حرکت می کند. بیان نسبیتی برای انرژی آن، مانند فوتون، است{\displaystyle E_{v}=pc,}که مقدار مولفه فضایی تکانه آن نیز می باشد. برای حفظ تکانه، میون همان مقدار مولفه فضایی تکانه نوترینو را دارد، اما در جهت مخالف.

تجزیه و تحلیل جبری انرژی این واکنش فروپاشی به صورت آنلاین در دسترس است، [47] بنابراین شکل 3-12b به جای آن یک راه حل نموداری ماشین حساب را ارائه می دهد. انرژی نوترینو 29.79 MeV است و انرژی میون 33.91 MeV - 29.79 MeV = 4.12 MeV است. بیشتر انرژی توسط نوترینویی با جرم نزدیک به صفر حمل می شود.

فراتر از اصول اولیه [ ویرایش ]

عناوین این بخش نسبت به بخش‌های قبل دشواری فنی بسیار بیشتری دارند و برای درک مقدمه فضازمان منحنی ضروری نیستند.

سرعت [ ویرایش ]

مقاله اصلی: سرعت

شکل 4-1a. پرتویی از دایره واحد x 2 + y 2 = 1 در نقطه (cos a , sin a ) , جایی که a دو برابر مساحت بین پرتو، دایره و محور x است.

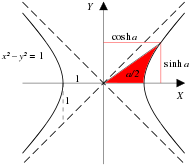
شکل 4-1b. پرتویی از هذلولی واحد x 2 − y 2 = 1 در نقطه (cosh a , sinh a ) , جایی که a دو برابر مساحت بین پرتو، هذلولی و محور x است.

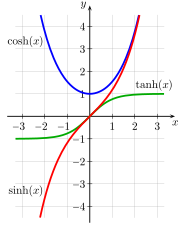
شکل 4-2. رسم سه تابع اصلی هیپربولیک : سینوس هذلولی ( sinh )، کسینوس هذلولی ( cosh ) و تانژانت هذلولی ( tanh ). سینه قرمز، کوش آبی و تنه سبز است.

تبدیل‌های لورنتس مختصات رویدادها را در یک چارچوب مرجع به یک چارچوب دیگر مرتبط می‌کند. ترکیب نسبیتی سرعت ها برای جمع دو سرعت با هم استفاده می شود. فرمول‌های انجام محاسبات اخیر غیرخطی هستند و آنها را پیچیده‌تر از فرمول‌های گالیله‌ای متناظر می‌کند.

این غیرخطی بودن یک مصنوع از انتخاب پارامترهای ما است. [7] : 47-59  قبلاً اشاره کرده‌ایم که در نمودار فضازمان x–ct ، نقاطی در فاصله زمانی ثابتی از مبدأ، یک هذلولی ثابت را تشکیل می‌دهند. همچنین اشاره کرده‌ایم که سیستم‌های مختصات دو قاب مرجع فضازمان در پیکربندی استاندارد به صورت هذلولی نسبت به یکدیگر می‌چرخند.

توابع طبیعی برای بیان این روابط، آنالوگ های هذلولی توابع مثلثاتی هستند . شکل 4-1a یک دایره واحد با sin( a ) و cos( a ) را نشان می دهد، تنها تفاوت بین این نمودار و دایره واحد آشنای مثلثات ابتدایی این است که a تفسیر می شود، نه به عنوان زاویه بین پرتو و x. - محور ، اما به اندازه دو برابر مساحت بخش که توسط پرتو از محور x خارج شده است. (از نظر عددی، اندازه‌های زاویه و مساحت 2 × برای دایره واحد یکسان هستند.) شکل 4-1b یک هذلولی واحد را با sinh( a ) و cosh( نشان می‌دهد.a )، که در آن a نیز دو برابر ناحیه رنگی تفسیر می شود. [48] ​​شکل 4-2 نمودارهایی از توابع sinh، cosh و tanh را نشان می دهد.

برای دایره واحد، شیب پرتو به دست می آید

{\displaystyle {\text{slope}}=\tan a={\frac {\sin a}{\cos a}}.}

در صفحه دکارتی، چرخش نقطه ( x , y ) به نقطه ( x ' , y ' ) با زاویه θ با

{\displaystyle {\begin{pmatrix}x'\\y'\\\end{pmatrix}}={\begin{pmatrix}\cos \theta &-\sin \theta \\\sin \theta &\cos \ تتا \\\end{pmatrix}}{\begin{pmatrix}x\\y\\\end{pmatrix}}.}

در نمودار فضا-زمان، پارامتر سرعت\بتاآنالوگ شیب است. سرعت ، φ ، با [41] تعریف می شود : 96-99 

{\displaystyle \beta \equiv \tanh \phi \equiv {\frac {v}{c}}،}

جایی که

{\displaystyle \tanh \phi ={\frac {\sinh \phi }{\cosh \phi }}={\frac {e^{\phi }-e^{-\phi }}{e^{\phi }+e^{-\phi }}}.}

سرعت تعریف شده در بالا در نسبیت خاص بسیار مفید است زیرا بسیاری از عبارات هنگامی که بر حسب آن بیان می شوند شکل بسیار ساده تری به خود می گیرند. برای مثال، سرعت در فرمول سرعت-افزودن خطی به سادگی افزودنی است. [7] : 47-59 

{\displaystyle \beta ={\frac {\beta _{1}+\beta _{2}}{1+\beta _{1}\beta _{2}}}=}{\displaystyle {\frac {\tanh \phi _{1}+\tanh \phi _{2}}{1+\tanh \phi _{1}\tanh \phi _{2}}}=}{\displaystyle \tanh(\phi _{1}+\phi _{2})،}

یا به عبارت دیگر{\displaystyle \phi =\phi _{1}+\phi _{2}.}

تبدیل های لورنتس زمانی که بر حسب سرعت بیان می شوند، شکل ساده ای به خود می گیرند. ضریب γ را می توان به صورت زیر نوشت

{\displaystyle \gamma ={\frac {1}{\sqrt {1-\beta ^{2}}}}={\frac {1}{\sqrt {1-\tanh ^{2}\phi }} }}{\displaystyle =\cosh \phi،}

{\displaystyle \gamma \beta ={\frac {\beta }{\sqrt {1-\beta ^{2}}}}={\frac {\tanh \phi }{\sqrt {1-\tanh ^{ 2}\phi }}}} {\displaystyle =\sinh \phi .}

تبدیل هایی که حرکت نسبی را با سرعت یکنواخت و بدون چرخش محورهای مختصات فضا توصیف می کنند، بوست نامیده می شوند.

با جایگزینی γ و γβ در تبدیل‌هایی که قبلاً ارائه شد و بازنویسی به شکل ماتریس، تقویت لورنتس در جهت x ممکن است به صورت نوشته شود.

{\displaystyle {\begin{pmatrix}ct'\\x'\end{pmatrix}}={\begin{pmatrix}\cosh \phi &-\sinh \phi \\-\sinh \phi &\cosh \phi \end{pmatrix}}{\begin{pmatrix}ct\\x\end{pmatrix}},}

و تقویت معکوس لورنتس در جهت x ممکن است به صورت نوشته شود

{\displaystyle {\begin{pmatrix}ct\\x\end{pmatrix}}={\begin{pmatrix}\cosh \phi &\sinh \phi \\\sinh \phi &\cosh \phi \end{pmatrix }}{\begin{pmatrix}ct'\\x'\end{pmatrix}}.}

به عبارت دیگر، بوست های لورنتس نشان دهنده چرخش های هذلولی در فضازمان مینکوفسکی است. [41] : 96-99 

مزایای استفاده از توابع هذلولی به حدی است که برخی از کتاب های درسی مانند کتاب های کلاسیک تیلور و ویلر استفاده از آنها را در مراحل اولیه معرفی می کنند. [7] [49] [یادداشت 12]

4-بردار [ ویرایش ]