تبدیل های لورنتس [ ویرایش ]

مقالات اصلی: تبدیل تبدیل های لورنتس و گروه لورنتس

دگرگونی‌های گالیله و متعاقب آن قانون عرف جمع سرعت‌ها در دنیای معمولی هواپیماها، ماشین‌ها و توپ‌ها با سرعت پایین به خوبی کار می‌کنند. با این حال، از اواسط دهه 1800، ابزار دقیق علمی حساس شروع به یافتن ناهنجاری‌هایی کردند که به خوبی با اضافه کردن سرعت‌ها مطابقت نداشتند.

تبدیل های لورنتس برای تبدیل مختصات یک رویداد از یک فریم به فریم دیگر در نسبیت خاص استفاده می شود.

عامل لورنتس در تبدیلات لورنتس ظاهر می شود:

{\displaystyle {\begin{aligned}t'&=\gamma \left(t-{\frac {vx}{c^{2}}}\right)\\x'&=\gamma \left(x- vt\right)\\y'&=y\\z'&=z\end{تراز شده}}}

تبدیل های معکوس لورنتس عبارتند از:

{\displaystyle {\begin{aligned}t&=\gamma \left(t'+{\frac {vx'}{c^{2}}}\right)\\x&=\gamma \left(x'+vt '\right)\\y&=y'\\z&=z'\end{تراز شده}}}

هنگامی که v ≪c و x به اندازه کافی کوچک هستند، ترم های v 2 / c 2 و vx / c 2 به صفر نزدیک می شوند و تبدیل های لورنتس تقریباً به تبدیل های گالیله می شوند.

{\displaystyle t'=\gamma (t-vx/c^{2})،}{\displaystyle x'=\گاما (x-vt)}و غیره، اغلب واقعاً معنی دارند{\displaystyle \Delta t'=\gamma (\Delta tv\Delta x/c^{2})،} {\displaystyle \Delta x'=\gamma (\Delta xv\Delta t)}اگر چه برای اختصار معادلات تبدیل لورنتز بدون دلتا نوشته می‌شوند، x به معنای Δ x و غیره است .

نامیدن یک مجموعه از تبدیل‌ها تبدیل‌های معمولی لورنتس و دیگری تبدیل‌های معکوس گمراه‌کننده است، زیرا هیچ تفاوت ذاتی بین فریم‌ها وجود ندارد. نویسندگان مختلف یک یا آن دسته از تبدیل ها را مجموعه «معکوس» می نامند. تبدیل‌های رو به جلو و معکوس به طور بی‌اهمیتی با یکدیگر مرتبط هستند، زیرا فریم S فقط می‌تواند با توجه به S به سمت جلو یا معکوس حرکت کند . بنابراین معکوس کردن معادلات به سادگی مستلزم تعویض متغیرهای اولیه و غیر آغاز شده و جایگزینی v با - v است. [41] : 71-79 

مثال: ترنس و استلا در مسابقه فضایی زمین تا مریخ هستند. ترنس یک مقام رسمی در خط شروع است، در حالی که استلا یک شرکت کننده است. در زمان t = t ′ = 0 ، سفینه فضایی استلا به سرعت تا 0.5 درجه سانتیگراد شتاب می گیرد . فاصله زمین تا مریخ 300 ثانیه نوری (حدود90.0 × 10 6 کیلومتر ). ترنس مشاهده می کند که استلا از ساعت خط پایان در t = 600.00 ثانیه عبور می کند. اما استلا زمان را در کرنومتر کشتی خود مشاهده می کند{\displaystyle t^{\prime }=\gamma \left(t-vx/c^{2}\right)=519.62\ {\text{s}}}همانطور که او از خط پایان عبور می کند، و فاصله بین خطوط شروع و پایان را که در کادر او اندازه گیری می شود، 259.81 ثانیه نوری (حدوداً) محاسبه می کند.77.9 × 10 6 کیلومتر ). 1).

استخراج تبدیلات لورنتس [ ویرایش ]

مقاله اصلی: مشتقات تبدیلات لورنتس

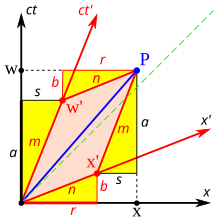
شکل 3-5. اشتقاق تبدیل لورنتس

از زمان کار اصلی اینشتین در سال 1905، ده‌ها اشتقاق از دگرگونی‌های لورنتس وجود داشته است که هر کدام تمرکز خاص خود را داشتند. اگرچه اشتقاق انیشتین مبتنی بر تغییرناپذیری سرعت نور بود، اصول فیزیکی دیگری نیز وجود دارد که ممکن است به عنوان نقطه شروع عمل کنند. در نهایت، این نقاط شروع جایگزین را می توان عبارات متفاوتی از اصل اساسی محلی بودن در نظر گرفت ، که بیان می کند تأثیری که یک ذره بر ذره دیگر اعمال می کند نمی تواند فوراً منتقل شود. [42]

اشتقاق داده شده در اینجا و نشان داده شده در شکل 3-5 بر اساس یکی ارائه شده توسط Bais [39] : 64-66  است و از نتایج قبلی از ترکیب نسبیتی سرعت ها، اتساع زمان و بخش های انقباض طول استفاده می کند. رویداد P دارای مختصات ( w , x ) در "سیستم استراحت" سیاه و مختصات ( w ′ , x " ) در کادر قرمز است که با پارامتر سرعت β = v / c در حال حرکت است . برای تعیین w و x بر حسب w و x(یا برعکس) در ابتدا استخراج تبدیل معکوس لورنتس آسان تر است.

  1. چیزی به نام انبساط/انقباض طول در جهات عرضی نمی تواند وجود داشته باشد. y باید برابر y و z باید برابر z باشد، در غیر این صورت این که یک توپ با سرعت 1 متری بتواند در یک سوراخ دایره ای 1 متری قرار بگیرد یا خیر، به ناظر بستگی دارد. فرض اول نسبیت بیان می کند که تمام قاب های اینرسی معادل هستند و انبساط/انقباض عرضی این قانون را نقض می کند. [41] : 27-28 

  2. از رسم، w = a + b و x = r + s

  3. از نتایج قبلی با استفاده از مثلث های مشابه، می دانیم که s / a = b / r = v / c = β .

  4. به دلیل اتساع زمان، a = γw ′

  5. با جایگزینی معادله (4) به s / a = β ، s = γw ′ β به دست می آید .

  6. انقباض طول و مثلث های مشابه به ما r = γx ' و b = βr = βγx ' می دهند.

  7. جایگزین کردن عبارات s ، a ، r و b در معادلات مرحله 2 بلافاصله نتیجه می دهد

    {\displaystyle w=\gamma w'+\beta \gamma x'}

    {\displaystyle x=\gamma x'+\beta \gamma w'}

معادلات فوق عبارات متناوب برای معادلات t و x تبدیل معکوس لورنتس هستند، همانطور که می توان با جایگزینی ct به جای w ، ct " به جای w " و v / c به جای β مشاهده کرد. از تبدیل معکوس می توان معادلات تبدیل رو به جلو را با حل t و x بدست آورد .