3-ریاضیات و هنر
نسبت طلایی [ ویرایش ]
اطلاعات بیشتر: فهرست آثار طراحی شده با نسبت طلایی
نسبت طلایی (تقریباً برابر با 1.618) برای اقلیدس شناخته شده بود . [38] نسبت طلایی به طور مداوم ادعا شده است [39] [40] [41] [42] در دوران مدرن که در هنر و معماری توسط قدیم در مصر، یونان و جاهای دیگر، بدون شواهد قابل اعتماد استفاده شده است. [43] این ادعا ممکن است ناشی از اشتباه گرفتن با «میانگین طلایی» باشد، که برای یونانیان باستان به معنای «پرهیز از افراط در هر جهت» بود، نه یک نسبت. [43] هرم شناسان از قرن 19 بر اساس دلایل ریاضی مشکوک برای نسبت طلایی در طراحی هرم بحث کرده اند. [ ب] پارتنون، یک معبد قرن 5 قبل از میلاد در آتن، ادعا شده است که از نسبت طلایی در نما و پلان کف خود استفاده می کند، [46] [47] [48] اما این ادعاها نیز با اندازه گیری رد می شوند. [43] مسجد بزرگ قیروان در تونس نیز به همین ترتیب ادعا شده است که از نسبت طلایی در طراحی خود استفاده می کند، [49] اما این نسبت در قسمت های اصلی مسجد دیده نمی شود. [50] مورخ معماری فردریک مکودی لوند در سال 1919 استدلال کرد که کلیسای جامع شارتر (قرن دوازدهم)، نوتردام لائون (1157-1205) و نوتردام پاریس(1160) با توجه به نسبت طلایی طراحی شده اند، [51] خطوط تنظیم کننده را برای ساختن کیس خود ترسیم می کنند. محققان دیگر استدلال می کنند که تا زمان کار پاچیولی در سال 1509، نسبت طلایی برای هنرمندان و معماران ناشناخته بود. [52] برای مثال، ارتفاع و عرض جلوی نوتردام لائون نسبت 8/5 یا 1.6 است، نه 1.618. تشخیص چنین نسبت های فیبوناچی از نسبت طلایی به سرعت دشوار می شود. [53] پس از پاچیولی، نسبت طلایی به طور قطع در آثار هنری از جمله مونالیزای لئوناردو قابل تشخیص است . [54]
نسبت دیگر، تنها عدد مورفیک دیگر، [55] در سال 1928 توسط معمار هلندی هانس ون در لاان (که در اصل به فرانسوی le nombre radiant نامیده می شد ) عدد پلاستیکی [c] نامگذاری شد. [56] مقدار آن حل معادله مکعب است

عددی غیر منطقی که تقریباً 1.325 است. به گفته معمار ریچارد پادووان ، این نسبت های مشخصی دارد3/4و1/7، که بر محدودیت های ادراک انسان در ارتباط یک اندازه فیزیکی به اندازه دیگر حاکم است. Van der Laan از این نسبت ها هنگام طراحی کلیسای ابی سنت بندیکتوسبرگ در سال 1967 در هلند استفاده کرد. [56]
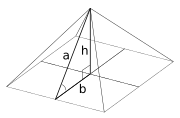
نسبت های پایه:هیپوتنوز(b:a) برای هرم خوفو می تواند: 1:φ ( مثلث کپلر )، 3:5 ( مثلث 3-4-5 )، یا 1:4/π باشد.
مستطیل های طلایی که بر روی مونالیزا قرار گرفته اند
کلیسای ابی سنت بندیکتوسبرگ در سال 1967 اثر Hans van der Laan دارای نسبت های اعداد پلاستیکی است .
تقارن های مسطح [ ویرایش ]
اطلاعات بیشتر: تقارن مسطح ، گروه کاغذ دیواری ، نقوش هندسی اسلیمی و گلیم
حضور قدرتمند: [57] فرش با مدال دوبل. آناتولی مرکزی (قونیه – کاراپینار)، نوبت قرن 16/17. مسجد علاءالدین
تقارن های مسطح برای هزاران سال در آثار هنری مانند فرش ، مشبک، منسوجات و کاشی کاری مورد استفاده قرار گرفته است. [58] [59] [60] [61]
بسیاری از قالیهای سنتی، چه فرشهای پرز و چه گلیمهای مسطح ، به یک زمین مرکزی و حاشیه قاببندی تقسیم میشوند. هر دو میتوانند تقارن داشته باشند، اگرچه در فرشهای دستبافت، این فرشها اغلب به دلیل جزئیات کوچک، تغییرات الگو و تغییر رنگ که توسط بافنده ایجاد میشود، کمی شکسته میشوند. [58] در گلیم های آناتولی ، نقوش به کار رفته خود معمولاً متقارن هستند. طرح کلی نیز معمولاً وجود دارد، با ترتیباتی مانند راه راه، راه راه متناوب با ردیف هایی از نقوش، و آرایه های بسته بندی شده از نقوش تقریباً شش ضلعی. این زمینه معمولاً به عنوان یک کاغذ دیواری با گروه کاغذ دیواری مانند pmm قرار می گیرد، در حالی که حاشیه ممکن است به عنوان یک گروه کاغذ دیواری طراحی شود.pm11، pmm2 یا pma2. گلیم های ترکیه و آسیای مرکزی اغلب دارای سه یا چند حاشیه در گروه های مختلف فریز هستند. بافندگان مطمئناً قصد تقارن داشتند، بدون دانش صریح از ریاضیات آن. [58] ریاضیدان و نظریهپرداز معماری نیکوس سالینگاروس پیشنهاد میکند که «حضور قدرتمند» [57] (اثر زیباییشناختی) یک «فرش عالی» [57] مانند بهترین فرشهای دو مدالی قونیه در قرن هفدهم توسط ریاضیات ایجاد شده است. تکنیک های مربوط به نظریه های معمار کریستوفر الکساندر. این تکنیک ها شامل جفت سازی متضادها است. مقادیر رنگ مخالف؛ تمایز نواحی از نظر هندسی، چه با استفاده از اشکال مکمل یا متعادل کردن جهت زوایای تیز. ارائه پیچیدگی در مقیاس کوچک (از سطح گره به بالا) و تقارن در مقیاس کوچک و بزرگ. تکرار عناصر در سلسله مراتبی از مقیاس های مختلف (با نسبت حدود 2.7 از هر سطح به سطح بعدی). سالینگاروس استدلال میکند که «همه فرشهای موفق حداقل ۹ قانون از ده قانون بالا را برآورده میکنند» و پیشنهاد میکند که ممکن است بتوان معیاری از این قوانین ایجاد کرد. [57]
مشبکهای استادانهای در کارهای جالی هندی یافت میشود که برای تزیین مقبرهها و کاخها در سنگ مرمر حکاکی شدهاند. [59] شبکه های چینی، همیشه با کمی تقارن، در 14 از 17 گروه کاغذ دیواری وجود دارد. آنها اغلب دارای آینه، آینه دوتایی یا تقارن چرخشی هستند. برخی دارای مدالیون مرکزی و برخی دارای حاشیه در گروه فریز هستند. [62] بسیاری از شبکه های چینی توسط Daniel S. Dye به صورت ریاضی تجزیه و تحلیل شده اند. او سیچوان را مرکز این صنعت میداند. [63]
تقارن ها در هنرهای نساجی از جمله لحاف کاری ، [60] بافندگی ، [64] دوخت متقاطع ، قلاب بافی ، [65] گلدوزی [66] [67] و بافندگی ، [68] که ممکن است صرفاً تزئینی باشند یا ممکن است نشانه هایی از وضعیت [69] تقارن چرخشی در ساختارهای دایره ای مانند گنبدها یافت می شود . اینها گاهی اوقات با نقشهای متقارن در داخل و خارج تزئین شده اند، مانند مسجد شیخ لطف الله اصفهان در سال 1619 . [70]اقلام گلدوزی و توری مانند رومیزی و حصیر رومیزی، که با استفاده از ماسوره یا با کتیبه ساخته می شوند ، می توانند طیف گسترده ای از تقارن های بازتابی و چرخشی داشته باشند که به صورت ریاضی در حال بررسی هستند. [71]
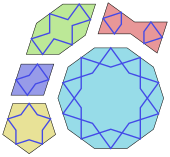
هنر اسلامی در بسیاری از هنرهای خود از تقارن بهره می برد، به ویژه در کاشی کاری. این ها با استفاده از مجموعه ای از پنج شکل کاشی، یعنی یک ده ضلعی منظم، یک شش ضلعی دراز، یک پاپیون، یک لوزی و یک پنج ضلعی منظم شکل می گیرند. تمام اضلاع این کاشی ها دارای طول یکسانی هستند. و تمام زوایای آنها مضرب 36 درجه (π/5 رادیان ) هستند که تقارن های پنج و ده برابری را ارائه می دهند. کاشی ها با خطوط تسمه ( girih ) تزئین شده اند که عموماً بیشتر از مرزهای کاشی قابل مشاهده است. در سال 2007، فیزیکدانان پیتر لو و پل استاینهارت استدلال کردند که گیره شبیه کاشیکاریهای شبه بلوری پنروز است. [72] هندسی استادانهکاشی کاری زلیج عنصری متمایز در معماری مراکشی است. [61] طاق های مقرنس سه بعدی هستند اما به صورت دو بعدی با نقشه هایی از سلول های هندسی طراحی شده اند. [73]
گلیم هوتامیس (جزئیات)، آناتولی مرکزی ، اوایل قرن نوزدهم
جزئیات یک پارچه ابریشمی سلسله مینگ ، با استفاده از الگوی مشبک شش ضلعی پخ
مشبک مرمر جاعلی در مقبره سلیم چشتی ، فاتح پور سیکری ، هند
سقف مسجد شیخ لطف الله ، اصفهان ، ۱۶۱۹م
تقارن چرخشی در توری : کار تات
کاشی های گیره : نقوش در مقیاس بزرگ و کوچک بر روی اسپندل از حرم درب امام ، اصفهان، 1453.
Tessellations : کاشی های موزاییک Zellige در مدرسه Bou Inania ، Fes ، مراکش
هندسه پیچیده و کاشیکاری مقرنس کاری های مسجد شیخ لطف الله اصفهان
نقشه معمار طاق ربع مقرنس. طومار توپکاپی
تونیک توپا اینکا از پرو ، 1450-1540، منسوجات آند نشان دهنده رتبه بالا [69]














![تونیک توپا اینکا از پرو، 1450-1540، منسوجات آند که نشان دهنده رتبه بالا است[69]](https://upload.wikimedia.org/wikipedia/commons/thumb/a/a2/Tupa-inca-tunic.png/152px-Tupa-inca-tunic.png)
 در این وبلاگ به ریاضیات و کاربردهای آن و تحقیقات در آنها پرداخته می شود. مطالب در این وبلاگ ترجمه سطحی و اولیه است و کامل نیست.در صورتی سوال یا نظری در زمینه ریاضیات دارید مطرح نمایید .در صورت امکان به آن می پردازم. من دوست دارم برای یافتن پاسخ به سوالات و حل پروژه های علمی با دیگران همکاری نمایم.در صورتی که شما هم بامن هم عقیده هستید با من تماس بگیرید.
در این وبلاگ به ریاضیات و کاربردهای آن و تحقیقات در آنها پرداخته می شود. مطالب در این وبلاگ ترجمه سطحی و اولیه است و کامل نیست.در صورتی سوال یا نظری در زمینه ریاضیات دارید مطرح نمایید .در صورت امکان به آن می پردازم. من دوست دارم برای یافتن پاسخ به سوالات و حل پروژه های علمی با دیگران همکاری نمایم.در صورتی که شما هم بامن هم عقیده هستید با من تماس بگیرید.