قانون فارادی [ ویرایش ]

جریان الکتریکی متناوب از طریق شیر برقی سمت چپ جریان می یابد و یک میدان مغناطیسی متغیر تولید می کند. این میدان با القای الکترومغناطیسی باعث می شود که جریان الکتریکی در حلقه سیم سمت راست جریان یابد.

گسترده ترین نسخه قانون فارادی می گوید:

نیروی محرکه الکتریکی در اطراف یک مسیر بسته برابر است با منفی نرخ زمانی تغییر شار مغناطیسی محصور شده توسط مسیر. [13] [14]

بیانیه ریاضی [ ویرایش ]

تعریف انتگرال سطح متکی بر تقسیم سطح Σ به عناصر سطحی کوچک است. هر عنصر با بردار d A با قدر مساحت عنصر و جهت نرمال عنصر همراه است و به سمت خارج (با توجه به جهت سطح) اشاره می کند.

برای یک حلقه سیم در یک میدان مغناطیسی ، شار مغناطیسی Φ B برای هر سطح Σ که مرز آن حلقه داده شده است، تعریف می شود. از آنجایی که ممکن است حلقه سیم در حال حرکت باشد، Σ( t ) را برای سطح می نویسیم. شار مغناطیسی انتگرال سطح است :

 

{\displaystyle \Phi _{B}=\iint _{\Sigma (t)}\mathbf {B} (t)\cdot \mathrm {d} \mathbf {A} \,,}که در آن d A عنصری از سطح سطح متحرک Σ( t ) است، B میدان مغناطیسی است، و B · d A یک محصول نقطه برداری بردار است که نشان دهنده عنصر شار از طریق d A است. به عبارت بصری تر، شار مغناطیسی از طریق حلقه سیم متناسب با تعداد خطوط میدان مغناطیسی است که از حلقه عبور می کنند.

 

هنگامی که شار تغییر می کند - به دلیل تغییر B ، یا به دلیل جابجایی یا تغییر شکل حلقه سیم، یا هر دو - قانون القایی فارادی می گوید که حلقه سیم یک emf به دست می آورد ، که به عنوان انرژی موجود از یک بار واحد تعریف می شود که یک بار به اطراف حرکت کرده است. حلقه سیم [15] : ch17  [16] [17] (برخی منابع تعریف را متفاوت بیان می کنند. این عبارت برای سازگاری با معادلات نسبیت خاص انتخاب شده است.) به طور معادل، ولتاژی است که با قطع سیم اندازه گیری می شود تا یک مدار باز ، و اتصال یک ولت متر به سرنخ ها.

قانون فارادی بیان می کند که emf با نرخ تغییر شار مغناطیسی نیز به دست می آید:

 

{\displaystyle {\mathcal {E}}=-{\frac {\mathrm {d} \Phi _{B}}{\mathrm {d} t}}،}جایی که{\mathcal {E}}نیروی الکتروموتور (emf) و Φ B شار مغناطیسی است .

 

جهت نیروی محرکه الکتریکی توسط قانون لنز مشخص شده است .

قوانین القای جریان های الکتریکی به شکل ریاضی توسط فرانتس ارنست نویمان در سال 1845 ایجاد شد. [18]

قانون فارادی حاوی اطلاعاتی در مورد روابط بین قدر و جهت متغیرهای آن است. با این حال، روابط بین جهت ها صریح نیست. آنها در فرمول ریاضی پنهان هستند.

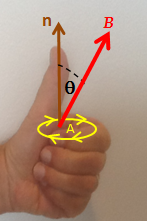
قانون دست چپ برای قانون فارادی. علامت ΔΦ B ، تغییر در شار، بر اساس رابطه بین میدان مغناطیسی B ، مساحت حلقه A ، و n نرمال به آن ناحیه، که با انگشتان دست چپ نشان داده می‌شود، پیدا می‌شود. اگر ΔΦ B مثبت باشد، جهت emf با انگشتان منحنی (سر پیکان زرد) یکسان است. اگر ΔΦ B منفی باشد، جهت emf بر خلاف نوک پیکان است. [19]

می توان جهت نیروی الکتروموتور (emf) را مستقیماً از قانون فارادی و بدون استناد به قانون لنز پی برد. یک قانون دست چپ به انجام این کار کمک می کند، به شرح زیر: [19] [20]

  • انگشتان منحنی دست چپ را با حلقه (خط زرد) تراز کنید.
  • شست خود را دراز کنید. انگشت شست کشیده شده جهت n (قهوه ای) را نشان می دهد که نسبت به ناحیه محصور شده توسط حلقه طبیعی است.
  • علامت ΔΦ B ، تغییر شار را پیدا کنید. شار اولیه و نهایی (که تفاوت آنها ΔΦ B است) را با توجه به n معمولی ، همانطور که با انگشت شست کشیده نشان داده می شود، تعیین کنید.
  • اگر تغییر در شار، ΔΦ B مثبت باشد، انگشتان منحنی جهت نیروی الکتروموتور را نشان می دهند (سر پیکان های زرد).
  • اگر ΔΦ B منفی باشد، جهت نیروی محرکه الکتریکی مخالف جهت انگشتان منحنی (برعکس نوک پیکان های زرد) است.

برای سیم پیچ محکمی از سیم ، متشکل از N دور یکسان، هر یک با همان Φ B ، قانون القای فارادی بیان می کند که [21] [22]

 

{\displaystyle {\mathcal {E}}=-N{\frac {\mathrm {d} \Phi _{B}}{\mathrm {d} t}}}که در آن N تعداد دور سیم و Φ B شار مغناطیسی از طریق یک حلقه است.

 

معادله ماکسول-فارادی [ ویرایش ]

 

تصویری از قضیه کلوین-استوکس با سطح Σ ، مرز آن ∂ Σ ، و جهت n که توسط قانون دست راست تنظیم شده است.

معادله ماکسول-فارادی بیان می‌کند که یک میدان مغناطیسی متغیر با زمان همیشه با یک میدان الکتریکی متغیر مکانی (همچنین احتمالاً متغیر با زمان)، غیر محافظه‌کار همراه است و بالعکس. معادله ماکسول-فارادی است

\nabla \times \mathbf {E} =-{\frac {\partial \mathbf {B} }{\partial t}}

(در واحدهای SI ) که در آن ∇ × عملگر curl و دوباره E ( r , t ) میدان الکتریکی و B ( r , t ) میدان مغناطیسی است . این فیلدها عموماً می توانند توابعی از موقعیت r و زمان t باشند. [23]

معادله ماکسول-فارادی یکی از چهار معادله ماکسول است و بنابراین نقش اساسی در نظریه الکترومغناطیس کلاسیک دارد. همچنین می‌توان آن را به شکل یکپارچه توسط قضیه کلوین-استوکس نوشت ، [24] و بدین ترتیب قانون فارادی را بازتولید کرد:

{\displaystyle \oint _{\partial \Sigma }\mathbf {E} \cdot \mathrm {d} \mathbf {l} =-\int _{\Sigma }{\frac {\partial \mathbf {B} } {\partial t}}\cdot \mathrm {d} \mathbf {A} }

همانطور که در شکل نشان داده شده است، Σ سطحی است که توسط کانتور بسته ∂ Σ محدود شده است ، dl یک عنصر برداری بینهایت کوچک از کانتور ∂Σ است ، و d A یک عنصر برداری بی نهایت کوچک از سطح Σ است. جهت آن متعامد به آن لکه سطحی است، قدر مساحت یک تکه بی نهایت کوچک از سطح است.

d l و d A هر دو دارای ابهام علامت هستند. برای به دست آوردن علامت صحیح ، همانطور که در مقاله قضیه کلوین-استوکس توضیح داده شد، از قانون دست راست استفاده می شود . برای یک سطح مسطح Σ ، یک عنصر مسیر مثبت d l منحنی ∂ Σ با قانون دست راست تعریف می شود که وقتی انگشت شست در جهت n نرمال به سطح Σ اشاره می کند با انگشتان دست راست اشاره می کند. .

خط انتگرال اطراف ∂ Σ را گردش خون می نامند . [15] : ch3  گردش غیر صفر E با رفتار میدان الکتریکی تولید شده توسط بارهای ساکن متفاوت است. یک میدان E تولید شده با بار را می توان به عنوان گرادیان میدان اسکالر که جواب معادله پواسون است و دارای یک انتگرال مسیر صفر است، بیان کرد. قضیه گرادیان را ببینید .

معادله انتگرال برای هر مسیر ∂ Σ در فضا، و هر سطح Σ که آن مسیر برای آن مرز است، صادق است.

اگر سطح Σ در زمان تغییر نکند، می توان معادله را بازنویسی کرد:

 

{\displaystyle \oint _{\partial \Sigma }\mathbf {E} \cdot \mathrm {d} \mathbf {l} =-{\frac {\mathrm {d} }{\mathrm {d} t}} \int _{\ Sigma }\mathbf {B} \cdot \mathrm {d} \mathbf {A} .}انتگرال سطح در سمت راست بیان صریح برای شار مغناطیسی Φ B تا Σ است.

 

میدان برداری الکتریکی القا شده توسط یک شار مغناطیسی در حال تغییر، جزء شیر برقی میدان الکتریکی کلی، را می توان در حد غیر نسبیتی با معادله انتگرال حجمی تقریب زد [23] : 321 

 

{\displaystyle \mathbf {E} _{s}(\mathbf {r} ,t)\approx -{\frac {1}{4\pi }}\iiint _{V}\ {\frac {\left( {\frac {\partial \mathbf {B} (\mathbf {r} ',t)}{\partial t}}\right)\times \left(\mathbf {r} -\mathbf {r} '\right )}{|\mathbf {r} -\mathbf {r} '|^{3}}}d^{3}\mathbf {r'} }