معادله دیفرانسیل بسل

معادله دیفرانسیل بسل یک معادله دیفرانسیل معمولی خطی مرتبه دوم است. این نام به افتخار ریاضیدان آلمانی فردریش ویلهلم بسل گرفته شد. راه حل های آنها توابع بسل یا توابع سیلندر نامیده می شوند .

فهرست

معادله دیفرانسیل بسل [ ویرایش | ویرایش منبع ]

معادله دیفرانسیل بسل یک معادله دیفرانسیل خطی معمولی مرتبه دوم است که توسط

$x^{2}{\frac {\mathrm {d} ^{2}f}{\mathrm {d} x^{2}}}+x{\frac {\mathrm {d} f}{ \mathrm {d} x}}+\left(x^{2}-\nu ^{2}\right)f=0$

تعریف شده است، جایی که $ایکس$ و $\nu$ اعداد حقیقی یا مختلط هستند. جواب ها را توابع بسل می نامند $\nu$ - مرتبه

به همین ترتیب، اپراتور بسل یک اپراتور دیفرانسیل درجه دوم است. تعریف شده است

$B_{\nu }:=x^{2}{\frac {{\mathrm d}^{2}}{{\mathrm d}x^{2}}}+x{\frac {{\mathrm d} {{\text{d}x}}+\left(x^{2}-\nu ^{2}\right)\,.$

با آن می توان به طور خلاصه معادله دیفرانسیل بسل را به صورت [1] بیان کرد.

$B_{\nu }f=0$

توابع بسل [ ویرایش | ویرایش منبع ]

عمومی [ ویرایش | ویرایش منبع ]

توابع بسل از نوع اول $J_{0},J_{1}$ $J_{2}$

توابع بسل از نوع دوم $Y_{0}،Y_{1}$ و $Y_2$

جواب های معادله دیفرانسیل بسل را توابع بسل می نامند . آنها نقش مهمی در فیزیک دارند، زیرا معادله دیفرانسیل بسل بخش شعاعی معادله لاپلاس را در مورد تقارن استوانه ای نشان می دهد. در میان چیزهای دیگر، هنگام بررسی ارتعاشات طبیعی یک غشاء دایره‌ای یا یک لوله ارگان، انتشار امواج آب در ظروف گرد، هدایت گرما در میله‌ها، تجزیه و تحلیل طیف فرکانسی سیگنال‌های مدوله‌شده با فرکانس ، با توابع بسل مواجه می‌شویم . توزیع میدان در مقطع موجبرهای دایره ایحالت های ساکن پتانسیل جعبه، توزیع توان در راکتورهای هسته ای ، شدت پراش نور در سوراخ های دایره ای و فیلترها در مهندسی برق ( فیلترهای بسل ). توابع بسل به دلیل کاربردهای متنوع آنها در فیزیک ریاضی جزو توابع ویژه محسوب می شوند .

به عنوان یک معادله دیفرانسیل مرتبه دوم، معادله دیفرانسیل بسل دارای دو راه حل مستقل خطی است . آنها را می توان به روش های مختلف توصیف کرد.

توابع بسل از نوع اول [ ویرایش | ویرایش منبع ]

توابع بسل $J_{\nu }$ جنس اول $\nu$ مرتبه به عنوان تعریف می شود

$J_{\nu }(x)=\sum _{r=0}^{\infty }{\frac {(-1)^{r}\left({\frac {x}{2}} \right)^{2r+\nu }}{\Gamma (\nu +r+1)r!}}\,$ ،

به موجب آن $\Gamma (\cdot )$ تابع گاما است . در مبدا ( $x=0$ ) این توابع برای اعداد صحیح هستند $\nu$ سرانجام.

برای اعداد غیر صحیح $\nu$ هستند $J_{\nu }$ و $J_{{-\nu }}$ راه حل های مستقل خطی

برای اعداد صحیح $\nu$ رابطه اعمال می شود

$J_{-\nu }(x)=(-1)^{\nu }J_{\nu }(x)=J_{\nu }(-x)\,$ .

در این مورد، دومین راه حل مستقل، تابع بسل نوع دوم است که در زیر مورد بحث قرار می گیرد.

نمایش های انتگرال [ ویرایش | ویرایش منبع ]

برای اعداد صحیح $\nu$ تابع بسل نوع اول را نیز می توان به عنوان یک انتگرال نشان داد:

${\begin{aligned}J_{\nu }(x)&={\frac {1}{\pi }}\int _{0}^{\pi }\cos(x\sin \varphi - \nu \varphi )\,\mathrm {d} \varphi \\&={\frac {1}{2\pi }}\int _{-\pi }^{\pi }e^{\mathrm {i } \,(x\sin \varphi -\nu \varphi )}\,\mathrm {d} \varphi \,.\end{تراز شده}}$

با آن است $J_{\nu }(x)$ را $\nu$ -امین ضریب فوریه تابع $\varphi \mapsto e^{ix\sin \varphi }$ .

تابع فوق هندسی [ ویرایش | ویرایش منبع ]

تابع بسل نوع اول را می توان با تابع فوق هندسی تعمیم یافته بیان کرد :

$J_{\nu }(x)={\frac {(x/2)^{\nu }}{\Gamma (\nu +1)}}\;_{0}F_{1}(; \nu +1;-x^{2}/4).$

این عبارت مربوط به بسط تابع بسل بر حسب تابع بسل-کلیفورد است .

توابع بسل از نوع دوم [ ویرایش | ویرایش منبع ]

همچنین توابع بسل از نوع دوم $Y_{\nu }(x)$ (که توابع وبر یا توابع نویمان نیز نامیده می شوند ) معادله دیفرانسیل بسل را حل می کنند. یک نام جایگزین است $N_{\nu }(x)$ . برای اعداد غیر صحیح $\nu$ میتوانی $Y_{\nu }(x)$ تعریف کردن توسط

$Y_{\nu }(x)={\frac {J_{\nu }(x)\cos(\nu \pi )-J_{{-\nu }}(x)}{\sin(\nu \pi )}}.$

برای اعداد صحیح $n$ عبور از گذرگاه مرزی است $\nu \nightarrow n$ تابع تشکیل شده است

$Y_{n}(x)=\lim _{{\nu \to n}}Y_{\nu }(x)$

به علاوه حل معادله دیفرانسیل بسل.

در مورد توابع بسل نوع اول، رابطه زیر برای توابع بسل نوع دوم نیز صادق است:

$Y_{{-n}}(x)=(-1)^{n}Y_{n}(x)$ .

پس از اجرای گذرگاه مرزی با قانون دی ال هاسپیتال نتایج

$Y_{n}(x)={\frac {1}{\pi }}\left[{\operatorname {d} \over \operatorname {d} \!\nu }J_{\nu }(x ){\Big |}_{\nu =n}+(-1)^{n}{\operatorname {d} \over \operatorname {d} \!\nu }J_{\nu }(x){\ بزرگ |}_{\nu =-n}\right].$

آدم صریح می یابد

$Y_{n}(x)=\,{\frac {2}{\pi }}\left(\gamma +\ln {\frac {x}{2}}\right)J_{n}( x)-{\frac {1}{\pi }}\sum _{k=0}^{n-1}{\frac {(nk-1)!}{k!}}\left({\frac {x}{2}}\right)^{2k-n}-{\frac {1}{\pi }}\sum _{k=0}^{\infty }(-1)^{k}{ \frac {H_{k}+H_{k+n}}{k!(n+k)!}}\left({\frac {x}{2}}\راست)^{2k+n}$

برای $n\in \mathbb {N} _{0}$ . اینجاست $\گاما$ ثابت اویلر-ماسکرونی و $H_{n}$ را $n$ -امین عدد هارمونیک

توابع بسل از نوع دوم در $x=0$ یک تکینگی لگاریتمی و یک قطب $n$ - مرتبه

برای همه $\nu$ از اولین نوع در کنار تابع بسل است $J_{\nu }$ تابع بسل از نوع دوم $Y_{\nu }$ راه حل دوم و مستقل خطی.

توابع بسل از نوع سوم [ ویرایش | ویرایش منبع ]

توابع بسل از نوع سوم $H_{\nu }^{{(1)}}$ ، $H_{\nu }^{{(2)}}$ (همچنین به عنوان توابع هانکل شناخته می شود) ترکیبات خطی توابع بسل از نوع اول و دوم هستند

${\begin{aligned}H_{\nu }^{{(1)}}(x)&=J_{\nu }(x)+{\mathrm{i}\cdot Y_{\nu }(x)\ , ,\\H_{\nu }^{{(2)}}(x)&=J_{\nu }(x)-{\text i}\cdot Y_{\nu }(x)\,,\ پایان {تراز شده}}$

به موجب آن $\mathrm {i}$ واحد موهومی را نشان می دهد . این دو تابع نیز راه حل های مستقل خطی معادله دیفرانسیل بسل هستند.

خواص [ ویرایش | ویرایش منبع ]

روابط راسته های یک جنس [ ویرایش | ویرایش منبع ]

برای توابع بسل $J_{\nu }$ ، $Y_{\nu }$ ، $H_{\nu }^{{(1)}}$ و $H_{\nu }^{{(2)}}$ روابط بازگشتی اعمال می شود :

${\frac {\nu }{x}}\Omega _{\nu }={\frac {1}{2}}(\Omega _{{\nu -1}}+\Omega _{{\nu + 1}})$ ،

${\frac {\rm {d}}{{\rm {d}}x}}\Omega _{\nu }={\frac {1}{2}}(\Omega _{\nu - 1}-\omega _{\nu +1})$ .

برای $x\in \mathbb {R}$ قابل اجرا است $\sum _{{n=-\infty }}^{\infty }J_{n}(x)^{2}=1$ .

برای $n\in \mathbb{N}$ قابل اجرا است $\left(-{\frac {1}{x}}{\frac {{{\rm {d}}}}{{{\rm {d}}}x}}\right)^{n}J_{ 0}(x)={\frac {J_{n}(x)}{x^{n}}}$ .

رفتار مجانبی [ ویرایش | ویرایش منبع ]

بودن $x,\nu \in \mathbb {R} ,\nu \geq 0$ ، سپس درخواست دهید $0<x\ll {\sqrt {\nu +1}}$ بازنمایی مجانبی

${\begin{تراز شده}J_{\nu }(x)&\approx {\frac {1}{\Gamma (\nu +1)}}\left({\frac {x}{2}}\راست) ^{\nu }\\Y_{\nu }(x)&\approx {\begin{cases}{\frac {2}{\pi }}\left(\ln \left({\frac {x}{ 2}}\right)+\gamma \right)&{\text{if }}\nu =0\\\\-{\frac {\Gamma (\nu )}{\pi }}\left({\ frac {2}{x}}\right)^{\nu }&{\text{if }}\nu >0.\end{cases}}\end{aligned}}$

برای بحث های بزرگ $x\gg |\nu ^{2}-1/4|$ یکی پیدا می کند

${\begin{aligned}J_{\nu }(x)&\approx {\sqrt {\frac {2}{\pi x}}}\cos \left(x-{\frac {\nu \ pi }{2}}-{\frac {\pi }{4}}\right)\\Y_{\nu }(x)&\approx {\sqrt {\frac {2}{\pi x}}} \sin \left(x-{\frac {\nu \pi }{2}}-{\frac {\pi }{4}}\right).\end{تراز شده}}$

این فرمول ها برای $\nu =1/2$ دقیقا. این را با توابع بسل کروی زیر مقایسه کنید.

توابع بسل اصلاح شده [ ویرایش | ویرایش منبع ]

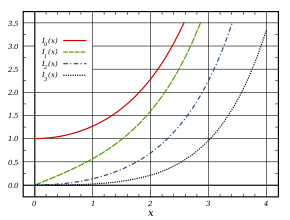
توابع بسل اصلاح شده از نوع اول برای $I_{0},I_{1},I_{2}$ و $من_{3}$

توابع بسل اصلاح شده از نوع دوم برای $K_{0},K_{1},K_{2}$ و $K_{3}$

معادله دیفرانسیل

$x^{2}{\frac {{\mathrm d}^{2}f}{{\mathrm d}x^{2}}}+x{\frac {{\mathrm d}f}{{\mathrm d}x}}-(x^{2}+\nu ^{2})f=0$

توسط توابع بسل با آرگومان های کاملاً موهومی حل می شود. توابع بسل اصلاح شده معمولاً برای حل آنها تعریف می شوند

${\begin{aligned}I_{\nu }(x)&=i^{{-\nu }}J_{\nu }(ix)=\sum _{{r=0}}^{\infty }{ \frac {({\frac {x}{2}})^{{2r+\nu }}}{\Gamma (r+\nu +1)r!}}\\K_{\nu }(x)&= {\frac {\pi }{2}}{\frac {I_{{-\nu }}(x)-I_{\nu }(x)}{\sin(\nu \pi )}}={\ frac {\pi }{2}}i^{{\nu +1}}H_{\nu }^{{(1)}}(ix)\\&={\frac {\pi }{2}} (-i)^{{\nu +1}}H_{\nu }^{{(2)}}(-ix)\end{تراز شده}}$

کارکرد $K_{\nu }(x)$ همچنین به عنوان تابع مک دونالد شناخته می شود . بر خلاف توابع بسل "عادی"، توابع بسل اصلاح شده یک رفتار نوسانی، بلکه یک رفتار نمایی از خود نشان نمی دهند.

انتگرال هوا [ ویرایش | ویرایش منبع ]

برای توابع $K_{1/3}}$ و $K_{2/3}}$ می توان یک نمایش یکپارچه ارائه داد

${\begin{aligned}K_{{1/3}}(x)&={\sqrt {3}}\int _{0}^{\infty }\cos \left({\frac {3}{2 }}x\left(u+{\frac {u^{3}}{3}}\right)\right){\mathrm d}u\\K_{{2/3}}(x)&={\ sqrt {3}}\int _{0}^{\infty }u\sin \left({\frac {3}{2}}x\left(u+{\frac {u^{3}}{3} }\right)\right){\mathrm d}u\end{تراز شده}}$ .

تابع فوق هندسی [ ویرایش | ویرایش منبع ]

تابع بسل اصلاح شده نوع اول را می توان با یک تابع فرا هندسی تعمیم یافته نیز بیان کرد :

$I_{\nu }(x)={\frac {(x/2)^{\nu }}{\Gamma (\nu +1)}}\;_{0}F_{1}(\nu +1 ;x^{2}/4)$ .

روابط راسته های یک جنس [ ویرایش | ویرایش منبع ]

برای توابع بسل $K_{\nu }$ و $I_{\nu }$ روابط بازگشتی اعمال می شود :

${\frac {\nu }{x}}K_{\nu }=-{\frac {1}{2}}\left(K_{\nu -1}-K_{\nu +1}\ درست)$

${\frac {\nu }{x}}I_{\nu }={\frac {1}{2}}\left(I_{\nu -1}-I_{\nu +1}\راست )$

${\frac {\rm {d}}{{\rm {d}}x}}K_{\nu }=-{\frac {1}{2}}(K_{\nu -1}+ K_{\nu +1})$

${\frac {\rm {d}}{{\rm {d}}x}}I_{\nu }={\frac {1}{2}}(I_{\nu -1}+I_ {\nu +1})$

رفتار مجانبی [ ویرایش | ویرایش منبع ]

ما دوباره این را فرض می کنیم $\nu$ واقعی و غیر منفی است. برای بحث های کوچک $0<x\ll {\sqrt {\nu +1}}$ یکی پیدا می کند

${\begin{aligned}I_{\nu }(x)&\approx {\frac {1}{\Gamma (\nu +1)}}\left({\frac {x}{2}} \right)^{\nu }\\\\K_{\nu }(x)&\approx {\begin{cases}-\left(\ln \left({\frac {x}{2}}}\ راست )+\گاما \راست)&{\text{if }}\nu =0\\\\{\frac {\Gamma (\nu )}{2}}\left({\frac {2}{x } }\right)^{\nu }&{\text{if }}\nu >0\,.\end{cases}}\end{تراز شده}}$

برای بحث های بزرگ $x\gg |\nu ^{2}-1/4|$ شما دریافت می کنید

${\begin{aligned}I_{\nu }(x)&\approx {\frac {1}{\sqrt {2\pi x}}}e^{x}\left(1+{\mathcal {O}}\left({\frac {1}{x}}\right)\right)\\\\K_{\nu }(x)&\approx {\sqrt {\frac {\pi }{2x }}}e^{-x}\left(1+{\mathcal {O}}\left({\frac {1}{x}}\right)\right)\,.\end{تراز شده}}$

توابع بسل کروی [ ویرایش | ویرایش منبع ]

پس از جداسازی متغیرها، معادله هلمهولتز در مختصات کروی به معادله شعاعی منتهی می شود.

$x^{2}{\frac {{\text{d}^{2}f_{\mu }(x)}{{\text{d}x^{2}}}+2x{\frac {{\ text{d} }f_{\mu }(x)}{\mathrm{d}x}}+[x^{2}-\mu (\mu +1)]f_{\mu }(x)=0$ .

بعد از تعویض

$f_{\mu }(x)={\frac {1}{{\sqrt {x}}}}u_{\mu }(x)$

معادله دیفرانسیل بسل بدست می آید $(\nu =\mu +1/2)$

$x^{2}{\frac {{\text{d}^{2}u_{\mu }(x)}{{\text{d}x^{2}}}+x{\frac {{\ text{d} }u_{\mu }(x)}{{\mathrm d}x}}+\left[x^{2}-\left(\mu +{\frac {1}{2}}\ راست)^{ 2}\right]u_{\mu }(x)=0$ .

برای راه حل $f_{\mu }(x)$ از معادله شعاعی معمولاً توابع بسل کروی هستند $j_{\mu }(x)$ ، توابع کروی نویمان $y_{\mu }(x)=n_{\mu }(x)$ و توابع کروی هانکل $h_{\mu }^{{(1،2)}}(x)$ تعریف می شوند:

${\begin{aligned}&j_{\mu }(x)\quad ={\sqrt {\frac {\pi }{2x}}}J_{\mu +1/2}(x)\\&y_ {\mu }(x)\quad ={\sqrt {\frac {\pi }{2x}}}Y_{\mu +1/2}(x)\\&h_{\mu }^{(1,2 )}(x)={\sqrt {\frac {\pi }{2x}}}H_{\mu +1/2}^{(1,2)}=j_{\mu }(x)\pm iy_ {\mu }(x)\end{تراز شده}}$ .

نمایندگی های جایگزین برای درخواست $m\in \mathbb{N}$

${\begin{aligned}&j_{m}(x)\quad =(-x)^{m}\left({\frac {1}{x}}{\frac {\mathrm {d} } } {\mathrm {d} x}}\right)^{m}\ {\frac {\sin x}{x}}\\&y_{m}(x)\quad =-(-x)^{m } \left({\frac {1}{x}}{\frac {\mathrm {d} }{\mathrm {d} x}}\right)^{m}\ {\frac {\cos x}{ x }}\\&h_{m}^{(1،2)}(x)=\mp i(-x)^{m}\left({\frac {1}{x}}{\frac {\ mathrm {d} }{\mathrm {d} x}}\right)^{m}{\frac {e^{\pm ix}}{x}}\\\end{تراز شده}}$

توابع کروی بسل و هانکل، به عنوان مثال، برای درمان چاه پتانسیل کروی متقارن در مکانیک کوانتومی مورد نیاز است .

خواص [ ویرایش | ویرایش منبع ]

برای توابع بسل کروی $j_{\mu }$ ، $y_{\mu }$ ، $h_{\mu }^{{(1)}}$ و $h_{\mu }^{{(2)}}$ روابط بازگشتی اعمال می شود :

${\begin{aligned}&{\frac {2\mu +1}{x}}\omega _{\mu }(x)\;\,=\omega _{\mu -1}(x ( x)-(\mu +1)\omega _{\mu +1}(x)\\&{\frac {\mathrm {d} }{\mathrm {d} x}}(x\omega _{\ mu }(x))\quad =x\omega _{\mu -1}(x)-\mu \omega _{\mu }(x)\end{تراز شده}}$ .

زیرا تعیین کننده Wronsky برقرار است

$W(j_{\mu },y_{\mu })={\frac {1}{i}}W(j_{\mu },h_{\mu }^{{(1)}})=-W (y_{\mu },h_{\mu }^{{(1)}})={\frac {1}{x^{2}}}$ .

تبدیل هانکل [ ویرایش | ویرایش منبع ]

→ مقاله اصلی : تبدیل هانکل

تبدیل هانکل یک تبدیل انتگرال است که ارتباط نزدیکی با تبدیل فوریه دارد. هسته انتگرال تبدیل Hankel تابع بسل از نوع اول است $Y_{n}$ ، یعنی عملگر انتگرال می خواند:

$H_{n}[f](s)=\int _{0}^{\infty }J_{n}(ts)tf(t){\mathrm{d}}t$ .

یک ویژگی خاص تبدیل هانکل این است که می توان از آن برای تبدیل عملگر بسل به یک عبارت جبری (یک ضرب) استفاده کرد.

تاریخچه [ ویرایش | ویرایش منبع ]

توابع بسل به تفصیل توسط بسل در سال 1824 مورد بحث قرار گرفت، [2] اما قبل از آن نیز برای مشکلات فیزیکی خاص ظاهر شدند، به عنوان مثال توسط دانیل برنولی (ارتعاش زنجیره سنگین 1738)، لئونارد اویلر (ارتعاش غشاء 1764)، در مکانیک آسمانی توسط جوزف . - لوئیس لاگرانژ (1770) و در پیر سیمون لاپلاس ، در هدایت گرما در جوزف فوریه (انتشار گرما در سیلندر 1822) و سیمئون دنیس پواسون (1823). [3] [4]

منبع

https://de.wikipedia.org/wiki/Besselsche_Differentialgleichung

+ نوشته شده در دوشنبه دوم خرداد ۱۴۰۱ ساعت 10:51 توسط علی رضا نقش نیلچی |

ریاضیات

آموزش ریاضی