از ویکیپدیا، دانشنامه آزاد

 

این مقاله در مورد نوسان ساز هارمونیک در مکانیک کلاسیک است. برای کاربردهای آن در مکانیک کوانتومی به نوسانگر هارمونیک کوانتومی مراجعه کنید .

بخشی از یک سریال در
مکانیک کلاسیک
{\displaystyle {\textbf {F}}={\frac {d}{dt}}(m{\textbf {v}})}

قانون دوم حرکت

نشان دادن

شاخه ها

نشان دادن

مبانی

نشان دادن

فرمولاسیون

پنهان شدن

موضوعات اصلی

نشان دادن

چرخش

نشان دادن

دانشمندان

در مکانیک کلاسیک ، یک نوسان ساز هارمونیک سیستمی است که وقتی از موقعیت تعادل خود جابجا می شود، نیروی بازگردانی F متناسب با جابجایی x را تجربه می کند :

 

{\displaystyle {\vec {F}}=-k{\vec {x}}،}   که در آن k ثابت مثبت است .

 

اگر F تنها نیروی وارد بر سیستم باشد، سیستم را یک نوسان ساز هارمونیک ساده می نامند و متحمل حرکت هارمونیک ساده می شود : نوسانات سینوسی حول نقطه تعادل، با دامنه ثابت و فرکانس ثابت (که به دامنه بستگی ندارد. ).

اگر نیروی اصطکاکی ( میرایی ) متناسب با سرعت نیز وجود داشته باشد، نوسانگر هارمونیک به عنوان یک نوسانگر میرا توصیف می شود . بسته به ضریب اصطکاک، سیستم می تواند:

حل  مرزی بین یک نوسان ساز کم میرایی و یک نوسانگر بیش از حد میرایی در مقدار خاصی از ضریب اصطکاک رخ می دهد و به آن میرا بحرانی می گویند .

اگر نیروی خارجی وابسته به زمان وجود داشته باشد، نوسان ساز هارمونیک به عنوان یک نوسانگر رانده توصیف می شود .

نمونه‌های مکانیکی شامل آونگ‌ها (با زوایای جابجایی کوچک )، جرم‌های متصل به فنرها و سیستم‌های صوتی است . سایر سیستم های مشابه شامل نوسانگرهای هارمونیک الکتریکی مانند مدارهای RLC می باشد . مدل نوسان ساز هارمونیک در فیزیک بسیار مهم است، زیرا هر جرمی که تحت یک نیروی در تعادل پایدار قرار می گیرد به عنوان یک نوسان ساز هارمونیک برای ارتعاشات کوچک عمل می کند. نوسانگرهای هارمونیک به طور گسترده در طبیعت وجود دارند و در بسیاری از دستگاه های دست ساز مانند ساعت ها و مدارهای رادیویی مورد استفاده قرار می گیرند. آنها تقریباً منبع تمام ارتعاشات و امواج سینوسی هستند.

 

فهرست

نوسان ساز هارمونیک ساده [ ویرایش ]

نوشتار اصلی: حرکت هارمونیک ساده

نوسان ساز هارمونیک چشمه جرم

حرکت هارمونیک ساده

یک نوسان ساز هارمونیک ساده نوسانگری است که نه رانده می شود و نه میرا . از یک جرم m تشکیل شده است که یک نیروی F را تجربه می کند که جرم را در جهت نقطه x = 0 می کشد و فقط به موقعیت x جرم و یک ثابت k بستگی دارد . موازنه نیروها ( قانون دوم نیوتن ) برای سیستم است

{\displaystyle F=ma=m{\frac {\mathrm {d} ^{2}x}{\mathrm {d} t^{2}}}=m{\ddot {x}}=-kx.}

 

با حل این معادله دیفرانسیل ، متوجه می شویم که حرکت توسط تابع توصیف می شود

 

{\displaystyle x(t)=A\cos(\omega t+\varphi)،}جایی که

 

{\displaystyle \omega ={\sqrt {\frac {k}{m}}}.}

 

حرکت تناوبی است و به صورت سینوسی با دامنه ثابت A تکرار می شود . علاوه بر دامنه آن، حرکت یک نوسان ساز هارمونیک ساده با دوره آن مشخص می شود.{\displaystyle T=2\pi /\omega }، زمان یک نوسان یا فرکانس آن{\displaystyle f=1/T}تعداد چرخه ها در واحد زمان. موقعیت در زمان معین t به فاز φ نیز بستگی دارد که نقطه شروع را در موج سینوسی تعیین می کند. دوره و فرکانس با اندازه جرم m و ثابت نیرو k تعیین می شود، در حالی که دامنه و فاز با موقعیت شروع و سرعت تعیین می شود .

سرعت و شتاب یک نوسان ساز هارمونیک ساده با همان فرکانس موقعیت، اما با فازهای جابجا شده، نوسان می کند. سرعت برای جابجایی صفر حداکثر است، در حالی که شتاب در جهت مخالف جابجایی است.

انرژی پتانسیل ذخیره شده در یک نوسان ساز هارمونیک ساده در موقعیت x برابر است

 

{\displaystyle U={\tfrac {1}{2}}kx^{2}.}

 

نوسانگر هارمونیک میرایی [ ویرایش ]

مقاله اصلی: میرایی

وابستگی رفتار سیستم به مقدار نسبت میرایی ζ

فایل: شتاب حرکت نوسانی.ogv

کلیپ ویدیویی که یک نوسان ساز هارمونیک میرا شده متشکل از یک چرخ دستی دینامیک بین دو فنر را نشان می دهد. یک شتاب سنج در بالای گاری بزرگی و جهت شتاب را نشان می دهد.

در اسیلاتورهای واقعی، اصطکاک یا میرایی، حرکت سیستم را کند می کند. به دلیل نیروی اصطکاک، سرعت متناسب با نیروی اصطکاک عمل کننده کاهش می یابد. در حالی که در یک نوسان ساز هارمونیک ساده بدون رانده تنها نیرویی که بر جرم وارد می شود نیروی بازگردان است، در یک نوسان ساز هارمونیک میرا شده نیروی اصطکاکی نیز وجود دارد که همیشه در جهت مخالف حرکت است. در بسیاری از سیستم‌های ارتعاشی، نیروی اصطکاک F f را می‌توان به‌عنوان متناسب با سرعت v جسم مدل‌سازی کرد: F f = - cv ، که در آن c ضریب میرایی ویسکوز نامیده می‌شود .

موازنه نیروها ( قانون دوم نیوتن ) برای نوسانگرهای هارمونیک میرا شده [1] [2] [3] است.

 

{\displaystyle F=-kx-c{\frac {\mathrm {d} x}{\mathrm {d} t}}=m{\frac {\mathrm {d} ^{2}x}{\mathrm { d} t^{2}}}،}   که می تواند در فرم بازنویسی شود

{\displaystyle {\frac {\mathrm {d} ^{2}x}{\mathrm {d} t^{2}}}+2\zeta \omega _{0}{\frac {\mathrm {d} x}{\mathrm {d} t}}+\omega _{0}^{2}x=0,}   جایی که

 

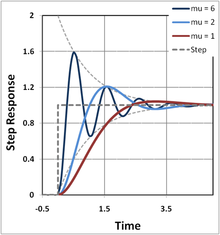
پاسخ مرحله ای یک نوسان ساز هارمونیک میرا شده. منحنی ها برای سه مقدار μ = ω 1 = ω 0 √ 1 −  ζ 2 رسم می شوند . زمان بر حسب واحد زمان فروپاشی τ = 1/( ζω 0 ) است.

مقدار نسبت میرایی ζ به طور بحرانی رفتار سیستم را تعیین می کند. یک نوسان ساز هارمونیک میرایی می تواند:

  • بیش از حد میرا شده ( ζ > 1): سیستم بدون نوسان به حالت ثابت برمی گردد (به صورت تصاعدی تحلیل می رود ). مقادیر بزرگتر نسبت میرایی ζ آهسته تر به حالت تعادل باز می گردند.
  • میرایی بحرانی ( ζ = 1): سیستم در سریع ترین زمان ممکن بدون نوسان به حالت ثابت باز می گردد (اگرچه اگر سرعت اولیه غیر صفر باشد می تواند بیش از حد اتفاق بیفتد). این اغلب برای میرایی سیستم هایی مانند درب ها مورد نظر است.
  • کم میرا ( ζ < 1): سیستم نوسان می کند (با فرکانس کمی متفاوت از حالت بدون میرا) با دامنه به تدریج به صفر کاهش می یابد. فرکانس زاویه ای نوسان ساز هارمونیک کم میرا شده توسط{\textstyle \omega _{1}=\omega _{0}{\sqrt {1-\zeta ^{2}}}،}واپاشی نمایی نوسان ساز هارمونیک کم میرا شده توسط داده می شود\lambda =\omega _{0}\zeta .

ضریب Q یک نوسان ساز میرا به صورت تعریف شده است

 

{\displaystyle Q=2\pi \times {\frac {\text{انرژی ذخیره شده}}{\text{انرژی از دست رفته در هر چرخه}}}.

 

Q با معادله به نسبت میرایی مربوط می شود{\textstyle Q={\frac {1}{2\zeta }}.}

نوسانگرهای هارمونیک رانده [ ویرایش ]

نوسانگرهای هارمونیک رانده، نوسانگرهای میرایی هستند که بیشتر تحت تأثیر نیروی اعمالی خارجی F ( t ) قرار می گیرند.

قانون دوم نیوتن شکل می گیرد

{\displaystyle F(t)-kx-c{\frac {\mathrm {d} x}{\mathrm {d} t}}=m{\frac {\mathrm {d} ^{2}x}{\ ریاضی {d} t^{2}}}.}

 

معمولاً در فرم بازنویسی می شود

 

{\displaystyle {\frac {\mathrm {d} ^{2}x}{\mathrm {d} t^{2}}}+2\zeta \omega _{0}{\frac {\mathrm {d} x}{\mathrm {d} t}}+\omega _{0}^{2}x={\frac {F(t)}{m}}.}

 

این معادله را می توان دقیقاً برای هر نیروی محرکه ای با استفاده از راه حل های z ( t ) که معادله غیراجباری را برآورده می کند حل کرد.

 

{\displaystyle {\frac {\mathrm {d} ^{2}z}{\mathrm {d} t^{2}}}+2\zeta \omega _{0}{\frac {\mathrm {d} z}{\mathrm {d} t}}+\omega _{0}^{2}z=0,}

 

و می توان آن را به صورت نوسانات سینوسی میرا بیان کرد:

 

{\displaystyle z(t)=Ae^{-\zeta \omega _{0}t}\sin \left({\sqrt {1-\zeta ^{2}}}\omega _{0}t+\varphi \درست)،}  در موردی که ζ ≤ 1 . دامنه A و فاز φ رفتار مورد نیاز برای مطابقت با شرایط اولیه را تعیین می کند.

 

ورودی مرحله ای [ ویرایش ]

همچنین ببینید: پاسخ گام

در حالت ζ < 1 و ورودی گام واحد با  x (0) = 0 :

 

{\displaystyle {\frac {F(t)}{m}}={\begin{cases}\omega _{0}^{2}&t\geq 0\\0&t<0\end{cases}}}راه حل این است

{\displaystyle x(t)=1-e^{-\zeta \omega _{0}t}{\frac {\sin \left({\sqrt {1-\zeta ^{2}}}\omega _ {0}t+\varphi \right)}{\sin(\varphi )}},}

 

با فاز φ داده شده توسط

 

{\displaystyle \cos \varphi =\zeta .}

 

زمانی که یک نوسانگر برای انطباق با شرایط خارجی تغییر یافته نیاز دارد، از مرتبه τ = 1/( ζω 0 ) است. در فیزیک، انطباق را آرامش و τ را زمان آرامش می نامند.

در مهندسی برق، مضرب τ ، زمان ته نشینی نامیده می شود ، یعنی زمان لازم برای اطمینان از اینکه سیگنال در یک انحراف ثابت از مقدار نهایی است، معمولاً در 10%. اصطلاح بیش از حد پاسخ به میزانی که حداکثر پاسخ از مقدار نهایی فراتر می رود، و کمترین میزان پاسخ به میزان کاهش پاسخ به زیر مقدار نهایی برای دفعات پس از حداکثر پاسخ اشاره دارد.

منبع

https://en.wikipedia.org/wiki/Harmonic_oscillator