ادامه 39 استفاده از قانون گاوس

محاسبات سطح و شار گاوسی

اکنون می‌توانیم از این شکل از میدان الکتریکی برای بدست آوردن شار میدان الکتریکی در سطح گاوس استفاده کنیم. برای تقارن کروی، سطح گاوسی یک سطح کروی بسته است که همان مرکز مرکز توزیع بار را دارد. بنابراین، جهت بردار مساحت یک عنصر ناحیه روی سطح گاوسی در هر نقطه موازی با جهت میدان الکتریکی در آن نقطه است، زیرا هر دو به صورت شعاعی به سمت بیرون هدایت می شوند ( (شکل) ).

میدان الکتریکی در هر نقطه از سطح گاوسی کروی برای توزیع بار متقارن کروی با بردار عنصر مساحت در آن نقطه موازی است و شار را به عنوان حاصلضرب بزرگی میدان الکتریکی و مقدار مساحت می دهد. توجه داشته باشید که شعاع R توزیع بار و شعاع r سطح گاوسی مقادیر متفاوتی هستند.

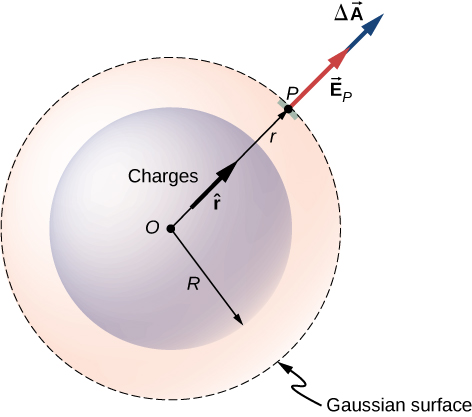
بزرگی میدان الکتریکی $\stackrel{\to }{\text{E}}$ باید در همه جای یک سطح کروی گوسی متحدالمرکز با توزیع یکسان باشد. برای یک سطح کروی به شعاع r ،

$\text{Φ}={\oint }_{S}{\stackrel{\to }{\text{E}}}_{P}·\stackrel{^}{\text{n}}\phantom{\ قانون{0.2em}{0ex}}dA={E}_{P}{\oint }_{S}\phantom{\rule{0.2em}{0ex}}dA={E}_{P}\phantom {\rule{0.2em}{0ex}}4\pi {r}^{2}.$

با استفاده از قانون گاوس

طبق قانون گاوس، شار از یک سطح بسته برابر است با کل بار محصور در سطح بسته تقسیم بر گذردهی خلاء ${\epsilon }_{0}$ . ${q}_{\text{enc}}$ مجموع بار محصور در فاصله r از مبدأ، که فضای داخل سطح کروی گاوسی با شعاع r است را در نظر بگیرید. این رابطه زیر را برای قانون گاوس به دست می دهد:

$4\pi {r}^{2}E=\frac{{q}_{\text{enc}}}{{\epsilon }_{0}}.$

از این رو، میدان الکتریکی در نقطه P که فاصله r از مرکز توزیع بار کروی متقارن است، دارای مقدار و جهت زیر است:

$\text{قدر:}\phantom{\rule{0.2em}{0ex}}E\left(r\right)=\frac{1}{4\pi {\epsilon }_{0}}\phantom{\ قانون{0.2em}{0ex}}\frac{{q}_{\text{enc}}}{{r}^{2}}$

جهت: شعاعی از O به P یا از P به O.

جهت میدان در نقطه P به مثبت یا منفی بودن بار در کره بستگی دارد. برای بار مثبت خالص محصور در سطح گاوسی، جهت از O به P است، و برای بار منفی خالص، جهت از P به O است. این تمام چیزی است که ما برای شارژ نقطه ای نیاز داریم، و متوجه خواهید شد که نتیجه بالا با نتیجه شارژ نقطه ای یکسان است. با این حال، قانون گاوس در مواردی که بار حجم محدودی را اشغال می کند واقعاً مفید است.

محاسبه شارژ محصور شده

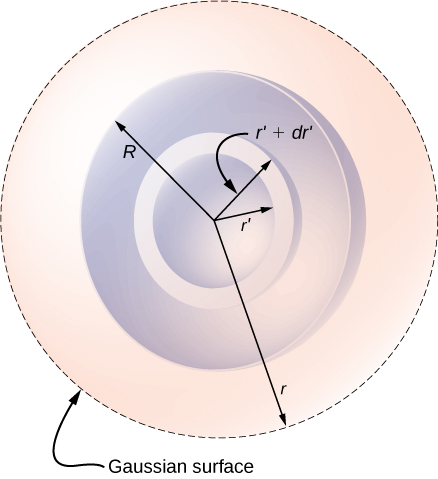
مورد جالب‌تر زمانی است که یک توزیع بار کروی حجمی را اشغال می‌کند، و پرسیدن اینکه میدان الکتریکی داخل توزیع بار چیست مرتبط می‌شود. در این مورد، بار محصور شده به فاصله r نقطه میدان نسبت به شعاع توزیع بار R بستگی دارد ، مانند آنچه در (شکل) نشان داده شده است.

یک توزیع بار کروی متقارن و سطح گاوسی که برای یافتن میدان (a) در داخل و (b) خارج از توزیع استفاده می شود.

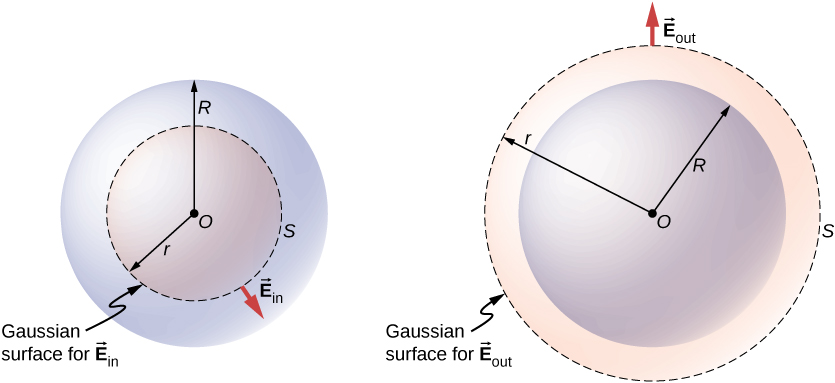
اگر نقطه P خارج از توزیع بار - یعنی اگر - قرار داشته باشد، $r\ge R$ سطح گاوسی حاوی P همه بارهای موجود در کره را در بر می گیرد. در این مورد، ${q}_{\text{enc}}$ برابر با بار کل در کره است. از طرف دیگر، اگر نقطه P در داخل توزیع بار کروی باشد، یعنی اگر سطح گاوسی یک کره کوچکتر از کره توزیع بار را در بر بگیرد. در این مورد، ${q}_{\text{enc}}$ کمتر از کل بار موجود در کره است. با مراجعه به (شکل) می توانیم ${q}_{\text{enc}}$ به صورت بنویسیم

${q}_{\text{enc}}=\left\{\begin{array}{c}{q}_{\text{tot}}\left(\text{total charge}\right)\phantom{ \rule{0.2em}{0ex}}\text{if}\phantom{\rule{0.2em}{0ex}}r\ge R\hfill \\ {q}_{\text{within}\phantom{\ rule{0.2em}{0ex}}r\phantom{\rule{0.2em}{0ex}}\text{<}\phantom{\rule{0.2em}{0ex}}R}\left(\text{فقط شارژ در}\phantom{\rule{0.2em}{0ex}}r\phantom{\rule{0.2em}{0ex}}\text{<}\phantom{\rule{0.2em}{0ex}}R\ راست)\phantom{\rule{0.2em}{0ex}}\text{if}\phantom{\rule{0.2em}{0ex}}r\phantom{\rule{0.2em}{0ex}}\text{ <}\phantom{\rule{0.2em}{0ex}}R\hfill \end{array}.$

میدان در یک نقطه خارج از توزیع بار ${\stackrel{\to }{\text{E}}}_{\text{out}}$ نیز نامیده می شود ، و میدان در یک نقطه در داخل توزیع بار ${\stackrel{\to }{\text{E}}}_{\text{in}}.$ نامیده می شود . میدان الکتریکی به عنوان

$P\phantom{\rule{0.2em}{0ex}}\text{outside sphere}\phantom{\rule{0.2em}{0ex}}{E}_{\text{out}}=\frac{1} {4\pi {\epsilon }_{0}}\phantom{\rule{0.2em}{0ex}}\frac{{q}_{\text{tot}}}{{r}^{2}}$

$P\phantom{\rule{0.2em}{0ex}}\text{inside sphere}\phantom{\rule{0.2em}{0ex}}{E}_{\text{in}}=\frac{1} {4\pi {\epsilon }_{0}}\phantom{\rule{0.2em}{0ex}}\frac{{q}_{\text{within}\phantom{\rule{0.2em}{0ex }}r\phantom{\rule{0.2em}{0ex}}\text{<}\phantom{\rule{0.2em}{0ex}}R}}{{r}^{2}}.$

توجه داشته باشید که میدان الکتریکی خارج از یک توزیع بار کروی متقارن با یک بار نقطه ای در مرکز یکسان است که باری برابر با بار کل توزیع بار کروی دارد. این قابل توجه است زیرا نقاط فقط در مرکز قرار ندارند. اکنون نمونه‌های خاصی از توزیع بار کروی را بررسی می‌کنیم، که با یک کره باردار یکنواخت شروع می‌کنیم.

کره باردار یکنواخت کره ای به شعاع R ، مانند آنچه در (شکل) نشان داده شده است، دارای چگالی بار حجمی یکنواخت است ${\rho }_{0}$ . میدان الکتریکی را در نقطه ای خارج از کره و در نقطه ای در داخل کره پیدا کنید.

استراتژی استراتژی حل مسئله قانون گاوس را اعمال کنید، جایی که ما قبلاً محاسبه شار را کار کرده ایم.

راه حل بار محصور شده توسط سطح گاوسی با داده می شود

${q}_{\text{enc}}={\int \rho }_{0}dV={\int }_{0}^{r}{\rho }_{0}4\pi {{r }^{\prime }}^{2}d{r}^{\prime }={\rho }_{0}\left(\frac{4}{3}\pi {r}^{3}\ درست).$

سپس پاسخ دامنه میدان الکتریکی را می توان بلافاصله برای یک نقطه خارج از کره، با برچسب ${E}_{\text{out}}،$ و یک نقطه در داخل کره، با برچسب نوشت. ${E}_{\text{in}}.$

$\begin{array}{ccc}\hfill {E}_{\text{out}}& =\hfill & \frac{1}{4\pi {\epsilon }_{0}}\phantom{\rule{ 0.2em}{0ex}}\frac{{q}_{\text{tot}}}{{r}^{2}},\phantom{\rule{0.2em}{0ex}}{q}_{ \text{tot}}=\frac{4}{3}\pi {R}^{3}\phantom{\rule{0.2em}{0ex}}{\rho }_{0},\hfill \\ \hfill {E}_{\text{in}}& =\hfill & \frac{{q}_{\text{enc}}}{4\pi {\epsilon }_{0}{r}^{ 2}}=\frac{{\rho }_{0}r}{3{\epsilon }_{0}},\phantom{\rule{0.2em}{0ex}}\text{since}\phantom{ \rule{0.2em}{0ex}}{q}_{\text{enc}}=\frac{4}{3}\pi {r}^{3}\phantom{\rule{0.2em}{0ex }}{\rho }_{0}.\hfill \end{array}$

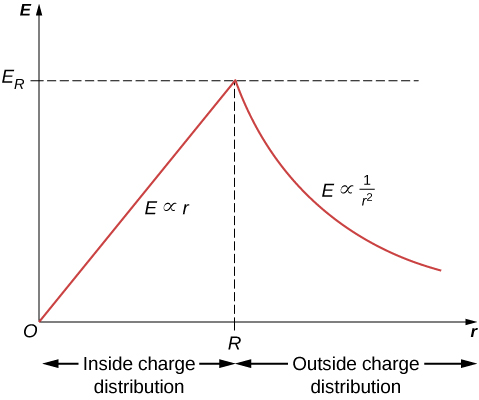
جالب است بدانید که اندازه میدان الکتریکی در داخل ماده با بیرون رفتن افزایش می یابد، زیرا مقدار بار محصور شده توسط سطح گاوسی با حجم افزایش می یابد. به طور خاص، بار محصور رشد می‌کند $\propto {r}^{3}$ ، در حالی که میدان هر عنصر بی‌نهایت کوچک بار کاهش $\propto 1\text{/}{r}^{2}$ می‌یابد و نتیجه خالص این است که میدان الکتریکی در توزیع به صورت خطی با شعاع افزایش می‌یابد. با دور شدن از بارها، قدر میدان الکتریکی خارج از کره کاهش می‌یابد، زیرا بار موجود ثابت می‌ماند اما فاصله افزایش می‌یابد. (شکل) تغییرات بزرگی میدان الکتریکی را با فاصله از مرکز یک کره با بار یکنواخت نشان می دهد.

میدان الکتریکی یک کره با بار یکنواخت و نارسانا در داخل کره به حداکثر در سطح افزایش می یابد و سپس به اندازه کاهش می یابد $1\text{/}{r}^{2}$ . اینجا، ${E}_{R}=\frac{{\rho }_{0}R}{3{\epsilon }_{0}}$ . میدان الکتریکی به دلیل توزیع بار کروی با چگالی بار یکنواخت و بار کل Q به عنوان تابعی از فاصله از مرکز توزیع است.

شکل نمودار E در مقابل r را نشان می دهد. منحنی در یک خط مستقیم با برچسب E متناسب با r بالا می رود، به اوج می رسد و در یک خط منحنی با برچسب E متناسب با 1 با r مربع می افتد. پیک دارای مقدار x R و مقدار ay زیرنویس E R است.

جهت میدان الکتریکی در هر نقطه P به صورت شعاعی از مبدأ به سمت خارج و اگر ${\rho }_{0}$ منفی است به سمت داخل (یعنی به سمت مرکز) ${\rho }_{0}$ است. میدان الکتریکی در برخی از نقاط فضایی نماینده در (شکل) نشان داده شده است که مختصات شعاعی r آن $r=R\text{/}2$ ، و و .

بردارهای میدان الکتریکی در داخل و خارج یک کره باردار یکنواخت.

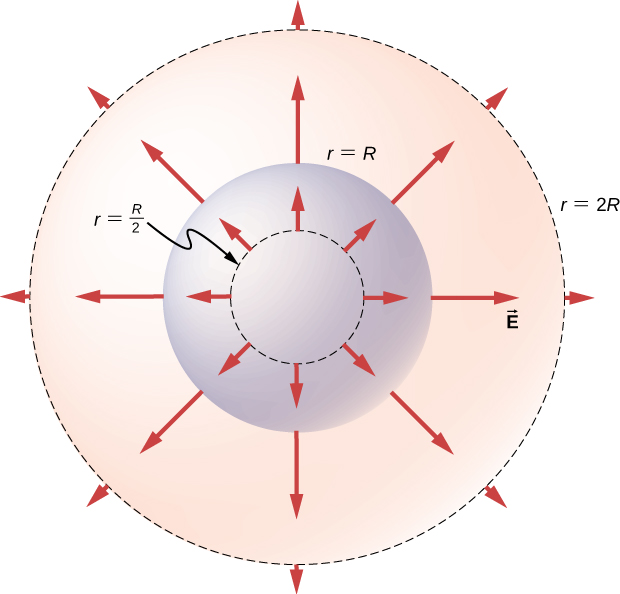
نکته مهم که ${E}_{\text{out}}$ شکلی مشابه معادله میدان الکتریکی یک بار نقطه ای ایزوله دارد. در تعیین میدان الکتریکی یک توزیع بار کروی یکنواخت، می‌توانیم فرض کنیم که تمام بار درون سطح گاوسی کروی مناسب در مرکز توزیع قرار دارد.

کره باردار غیر یکنواخت یک کره نارسانا با شعاع R دارای چگالی بار غیریکنواختی است که با فاصله از مرکز آن همانطور که توسط داده می شود تغییر می کند.

$\rho \left(r\right)=a{r}^{n}\phantom{\rule{0.2em}{0ex}}\left(r\le R;n\ge 0\راست)،$

جایی که a یک ثابت است. ما نیاز داریم $n\ge 0$ تا چگالی شارژ در تعریف نشده نباشد . میدان الکتریکی را در نقطه ای خارج از کره و در نقطه ای در داخل کره پیدا کنید.

استراتژی استراتژی قانون گاوس را که در بالا ارائه شده است، اعمال کنید، جایی که ما انتگرال های بار محصور شده را به طور جداگانه برای موارد داخل و خارج کره کار می کنیم.

راه حل از آنجایی که تابع چگالی بار داده شده فقط یک وابستگی شعاعی دارد و هیچ وابستگی به جهت ندارد، ما یک موقعیت کروی متقارن داریم. بنابراین، بزرگی میدان الکتریکی در هر نقطه در بالا آورده شده و جهت آن شعاعی است. ما فقط باید شارژ محصور شده را پیدا کنیم ${q}_{\text{enc}}،$ که به محل نقطه میدان بستگی دارد.

نکته ای در مورد نمادها: ما ${r}^{\prime }$ برای مکان یابی بارها در توزیع بار و r برای مکان یابی نقطه(های) میدان در سطح(های) گوسی استفاده می کنیم. از حرف R برای شعاع توزیع بار استفاده می شود.

از آنجایی که چگالی بار در اینجا ثابت نیست، باید تابع چگالی بار را روی حجم محصور شده توسط سطح گاوسی ادغام کنیم. بنابراین، ما مشکل را برای بارها در یک پوسته کروی، مثلاً بین ${r}^{\prime }$ و ${r}^{\prime }+d{r}^{\prime }،$ همانطور که در (شکل) نشان داده شده است، تنظیم می کنیم . حجم بارهای موجود در پوسته با عرض بینهایت کوچک برابر است با حاصل ضرب مساحت سطح $4\pi {{r}^{\prime }}^{2}$ و ضخامت $d{r}^{\prime }$ . ضرب حجم با چگالی در این مکان، که برابر است $a{{r}^{\prime }}^{n}$ ، شارژ را در پوسته به دست می‌دهد:

$dq=a{{r}^{\prime }}^{n}\phantom{\rule{0.2em}{0ex}}4\pi {{r}^{\prime }}^{2}d{r }^{\prime }.$

تقارن کروی با توزیع بار غیر یکنواخت. در این نوع مسائل به چهار شعاع نیاز داریم: R شعاع توزیع بار، r شعاع سطح گاوسی، ${r}^{\prime }$ شعاع داخلی پوسته کروی و ${r}^{\prime }+d{r}^{\prime }$ شعاع بیرونی پوسته کروی است. پوسته کروی برای محاسبه بار محصور در سطح گاوسی استفاده می شود. محدوده برای ${r}^{\prime }$ از 0 تا r برای میدان در نقطه ای در داخل توزیع بار و از 0 تا R برای میدان در نقطه ای خارج از توزیع بار است. اگر ، سطح گاوسی حجم بیشتری نسبت به توزیع بار را در بر می گیرد، اما حجم اضافی به ${q}_{\text{enc}}$ .

شکل چهار دایره متحدالمرکز را نشان می دهد. با شروع از کوچکترین، شعاع آنها با برچسب: r اول، r اول به علاوه dr prime، R و r. بیرونی ترین دایره نقطه چین است و سطح گاوسی نامگذاری شده است.

(الف) میدان در نقطه ای خارج از توزیع بار. در این حالت، سطح گاوسی که حاوی نقطه میدان P است، دارای شعاع r است که بزرگتر از شعاع R توزیع بار است . بنابراین، تمام بارهای توزیع بار در سطح گاوسی محصور می شوند. توجه داشته باشید که فضای بین ${r}^{\prime }=R$ و ${r}^{\prime }=r$ خالی از بار است و بنابراین به انتگرال بیش از حجم محصور شده توسط سطح گاوسی کمک نمی کند:

${q}_{\text{enc}}=\int \phantom{\rule{0.2em}{0ex}}dq={\int }_{0}^{R}\phantom{\rule{0.2em} {0ex}}a{{r}^{\prime }}^{n}\phantom{\rule{0.2em}{0ex}}4\pi {{r}^{\prime }}^{2}d {r}^{\prime }=\frac{4\pi a}{n+3}{R}^{n+3}.$

این در نتیجه کلی برای ${\stackrel{\to }{\text{E}}}_{\text{out}}$ به دست آوردن میدان الکتریکی در نقطه ای خارج از توزیع بار استفاده می شود

${\stackrel{\to }{\text{E}}}_{\text{out}}=\left[\frac{a{R}^{n+3}}{{\epsilon }_{0} \left(n+3\right)}\right]\frac{1}{{r}^{2}}\stackrel{^}{\text{r}}،$

جایی $\stackrel{^}{\text{r}}$ که یک بردار واحد در جهت مبدأ تا نقطه میدان در سطح گاوسی است.

(ب) در یک نقطه در داخل توزیع بار. سطح گاوسی اکنون در داخل توزیع بار مدفون شده است، با . بنابراین، فقط آن دسته از بارها در توزیع که در فاصله r از مرکز توزیع بار کروی قرار دارند در موارد زیر محاسبه می شوند ${r}_{\text{enc}}$ :

${q}_{\text{enc}}={\int }_{0}^{r}a{{r}^{\prime }}^{n}4\pi {{r}^{\prime }}^{2}\phantom{\rule{0.2em}{0ex}}d{r}^{\prime }=\frac{4\pi a}{n+3}{r}^{n+3 }.$

اکنون، با استفاده از نتیجه کلی بالا ${\stackrel{\to }{\text{E}}}_{\text{in}}،$ ، میدان الکتریکی را در نقطه ای می یابیم که فاصله r از مرکز است و در توزیع بار به صورت قرار دارد.

${\stackrel{\to }{\text{E}}}_{\text{in}}=\left[\frac{a}{{\epsilon }_{0}\left(n+3\راست) }\right]{r}^{n+1}\stackrel{^}{\text{r}}،$

که در آن اطلاعات جهت با استفاده از بردار شعاعی واحد گنجانده شده است.

درک خود را بررسی کنید بررسی کنید که میدان های الکتریکی کره به مقادیر صحیح برای بار نقطه ای کاهش یابد.

در این مورد فقط وجود دارد ${\stackrel{\to }{\text{E}}}_{\text{out}}.\phantom{\rule{0.2em}{0ex}}\text{So}،\text{yes}.$

+ نوشته شده در شنبه ششم فروردین ۱۴۰۱ ساعت 13:43 توسط علی رضا نقش نیلچی |

ریاضیات

آموزش ریاضی

ادامه 39 استفاده از قانون گاوس

پیوندهای روزانه

نوشته‌های پیشین

آرشیو موضوعی

پیوندها

آمارگیر وبلاگ

کد پربازدیدترین