در پایان این بخش، شما قادر خواهید بود:

  • تقارن کروی، استوانه ای و مسطح را توضیح دهید
  • تشخیص اینکه آیا یک سیستم معین یکی از این تقارن ها را دارد یا خیر
  • از قانون گاوس برای تعیین میدان الکتریکی یک سیستم با یکی از این تقارن ها استفاده کنید

قانون گاوس در تعیین عبارات میدان الکتریکی بسیار مفید است، حتی اگر قانون مستقیماً در مورد میدان الکتریکی نیست. این در مورد شار الکتریکی است. معلوم می‌شود که در موقعیت‌هایی که دارای تقارن‌های خاصی (کروی، استوانه‌ای یا مسطح) در توزیع بار هستند، می‌توانیم میدان الکتریکی را بر اساس دانش شار الکتریکی استنتاج کنیم. در این سیستم‌ها، می‌توانیم یک سطح گاوسی S را پیدا کنیم که میدان الکتریکی روی آن دارای قدر ثابت است. علاوه بر این، اگر با همه جای سطح \stackrel{\to }{\text{E}}موازی است، پس (اگر و در همه جای سطح ضد موازی هستند، پس ) قانون گاوس پس از آن ساده می شود\stackrel{^}{\text{n}}\stackrel{\to }{\text{E}}·\stackrel{^}{\text{n}}=E.\stackrel{\to }{\text{E}}\stackrel{^}{\text{n}}\stackrel{\to }{\text{E}}·\stackrel{^}{\text{n}}=\text{−}E.

\text{Φ}={\oint }_{S}\stackrel{\to }{\text{E}}·\stackrel{^}{\text{n}}\phantom{\rule{0.2em}{ 0ex}}dA=E{\oint }_{S}\phantom{\rule{0.2em}{0ex}}dA=EA=\frac{{q}_{\text{enc}}}{{\epsilon }_{0}}،

که در آن A مساحت سطح است. توجه داشته باشید که این تقارن ها منجر به تبدیل انتگرال شار به حاصل ضرب بزرگی میدان الکتریکی و ناحیه مناسب می شود. وقتی از این شار در بیان قانون گاوس استفاده می کنید، یک معادله جبری به دست می آورید که می توانید آن را برای بزرگی میدان الکتریکی حل کنید، که به نظر می رسد

E~\frac{{q}_{\text{enc}}}{{\epsilon }_{0}\phantom{\rule{0.2em}{0ex}}\text{area}}.

جهت میدان الکتریکی در نقطه میدان P از تقارن توزیع بار و نوع بار در توزیع به دست می آید. بنابراین، قانون گاوس می تواند برای تعیین استفاده شود \stackrel{\to }{\text{E}}.در اینجا خلاصه ای از مراحلی است که دنبال خواهیم کرد:

استراتژی حل مسئله: قانون گاوس

  1. تقارن فضایی توزیع بار را شناسایی کنید . این اولین قدم مهمی است که به ما امکان می دهد سطح گاوسی مناسب را انتخاب کنیم. به عنوان مثال، یک بار نقطه ای جدا شده دارای تقارن کروی است و یک خط بار بی نهایت دارای تقارن استوانه ای است.
  2. یک سطح گاوسی با تقارن مشابه با توزیع بار انتخاب کنید و پیامدهای آن را شناسایی کنید. با این انتخاب، \stackrel{\to }{\text{E}}·\stackrel{^}{\text{n}}به راحتی بر روی سطح گاوس تعیین می شود.
  3. انتگرال {\oint }_{S}\stackrel{\to }{\text{E}}·\stackrel{^}{\text{n}}\phantom{\rule{0.2em}{0ex}}dAرا روی سطح گاوسی ارزیابی کنید، یعنی شار را در سطح محاسبه کنید . تقارن سطح گاوسی به ما امکان می دهد تا \stackrel{\to }{\text{E}}·\stackrel{^}{\text{n}}خارج از انتگرال فاکتور بگیریم.
  4. مقدار بار محصور شده توسط سطح گاوسی را تعیین کنید . این یک ارزیابی از سمت راست معادله است که قانون گاوس را نشان می دهد. اغلب لازم است که یک ادغام انجام شود تا شارژ خالص محصور شود.
  5. میدان الکتریکی توزیع بار را ارزیابی کنید . اکنون می توان با استفاده از نتایج مراحل 3 و 4 این فیلد را پیدا کرد.

اساساً، تنها سه نوع تقارن وجود دارد که به قانون گاوس اجازه می دهد برای استنتاج میدان الکتریکی استفاده شود. آن ها هستند

  • توزیع بار با تقارن کروی
  • توزیع بار با تقارن استوانه ای
  • توزیع بار با تقارن مسطح

برای بهره‌برداری از تقارن، محاسبات را در سیستم‌های مختصات مناسب انجام می‌دهیم و از نوع مناسب سطح گاوسی برای آن تقارن استفاده می‌کنیم و چهار مرحله باقی‌مانده را اعمال می‌کنیم.

توزیع بار با تقارن کروی

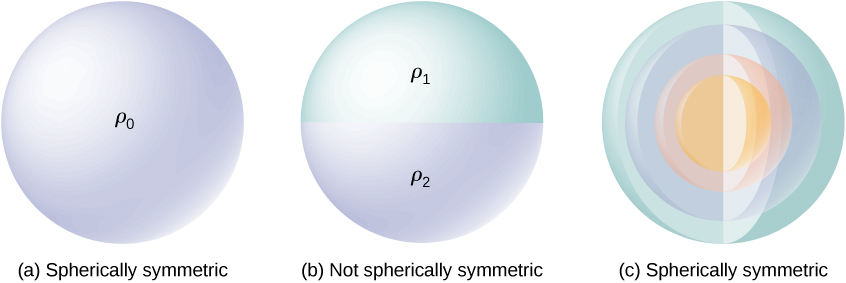
توزیع بار دارای تقارن کروی است اگر چگالی بار فقط به فاصله از یک نقطه در فضا بستگی داشته باشد نه به جهت. به عبارت دیگر، اگر سیستم را بچرخانید، ظاهر متفاوتی ندارد. به عنوان مثال، اگر یک کره با شعاع R به طور یکنواخت با چگالی بار بار شده باشد {\rho }_{0}، توزیع دارای تقارن کروی است ( (شکل) (الف)). از طرف دیگر، اگر کره ای با شعاع R به گونه ای بار شود که نیمه بالایی کره دارای چگالی بار یکنواخت {\rho }_{1}و نیمه پایینی دارای چگالی بار یکنواخت باشد {\rho }_{2}\ne {\rho }_{1}،، کره تقارن کروی ندارد زیرا چگالی بار به جهت بستگی دارد. ( (شکل)(ب)). بنابراین، این شکل جسم نیست، بلکه شکل توزیع بار است که تعیین می کند آیا یک سیستم تقارن کروی دارد یا خیر.

(شکل) (ج) کره ای را با چهار پوسته مختلف نشان می دهد که هر کدام چگالی بار یکنواخت خود را دارند. اگرچه این وضعیتی است که در آن چگالی بار در کره کامل یکنواخت نیست، تابع چگالی بار فقط به فاصله از مرکز بستگی دارد نه به جهت. بنابراین، این توزیع بار دارای تقارن کروی است.

تصاویر سیستم های کروی متقارن و غیر متقارن. سایه های مختلف نشان دهنده چگالی بار متفاوت است. بارهای روی اجسام کروی شکل لزوماً به این معنی نیست که بارها با تقارن کروی توزیع شده اند. تقارن کروی تنها زمانی رخ می دهد که چگالی بار به جهت بستگی نداشته باشد. در (الف)، بارها به طور یکنواخت در یک کره توزیع می شوند. در (ب)، نیمه بالایی کره دارای چگالی بار متفاوتی نسبت به نیمه پایینی است. بنابراین، (ب) تقارن کروی ندارد. در (c)، بارها در پوسته‌های کروی با چگالی بار متفاوت هستند، به این معنی که چگالی بار تنها تابعی از فاصله شعاعی از مرکز است. بنابراین، سیستم دارای تقارن کروی است.

شکل a یک کره یکنواخت رنگ با برچسب rho 0 را نشان می دهد. شکل به صورت کروی متقارن برچسب گذاری شده است. شکل b کره ای را نشان می دهد که نیمه های بالا و پایین آن رنگ های متفاوتی دارند. نیمکره بالایی با برچسب rho 1 و نیمکره پایینی با برچسب rho 2 مشخص شده است. این شکل دارای برچسب متقارن کروی نیست. شکل c یک کره را نشان می دهد که برش داده شده تا بسیاری از کره های متحدالمرکز با رنگ های مختلف را در داخل آن نشان دهد. شکل به صورت کروی متقارن برچسب گذاری شده است.

یک راه خوب برای تعیین اینکه آیا مسئله شما تقارن کروی دارد یا خیر این است که به تابع چگالی بار در مختصات کروی نگاه کنید \rho \left(r,\theta,\varphi \راست). اگر چگالی بار فقط تابعی از r باشد، یعنی \rho =\rho \چپ(r\راست)تقارن کروی دارید. تتااگر چگالی به یا بستگی دارد \varphi، می توانید آن را با چرخش تغییر دهید. بنابراین، شما تقارن کروی نخواهید داشت.

پیامدهای تقارن

در تمام موارد متقارن کروی، میدان الکتریکی در هر نقطه باید به صورت شعاعی جهت داده شود، زیرا بار و در نتیجه میدان باید تحت چرخش ثابت باشد. بنابراین، با استفاده از مختصات کروی با مبدأ آنها در مرکز توزیع بار کروی، می‌توان شکل مورد انتظار میدان الکتریکی را در نقطه P که در فاصله r از مرکز قرار دارد، یادداشت کرد:

\text{تقارن کروی:}\phantom{\rule{0.2em}{0ex}}{\stackrel{\to }{\text{E}}}_{P}={E}_{P}\left( r\right)\stackrel{^}{\text{r}}،

بردار \stackrel{^}{\text{r}}واحد در جهت از مبدأ تا نقطه میدان P نشان داده شده است. مولفه شعاعی {E}_{P}میدان الکتریکی می تواند مثبت یا منفی باشد. زمانی {E}_{P}>0،که میدان الکتریکی در P به دور از مبدأ، و زمانی که {E}_{P}<0،میدان الکتریکی در P به سمت مبدا اشاره می کند.

منبع

https://opentextbc.ca/universityphysicsv2openstax/chapter/applying-gausss-law/