ریاضیات

فرض کنید که یک تابع f در یک دامنه تحلیلی است و اجازه دهید C نشان دهنده هر کانتور بسته ساده مثبت گرا حول z 0 باشد که در آن دامنه قرار دارد. سپس در هر z در دامنه 

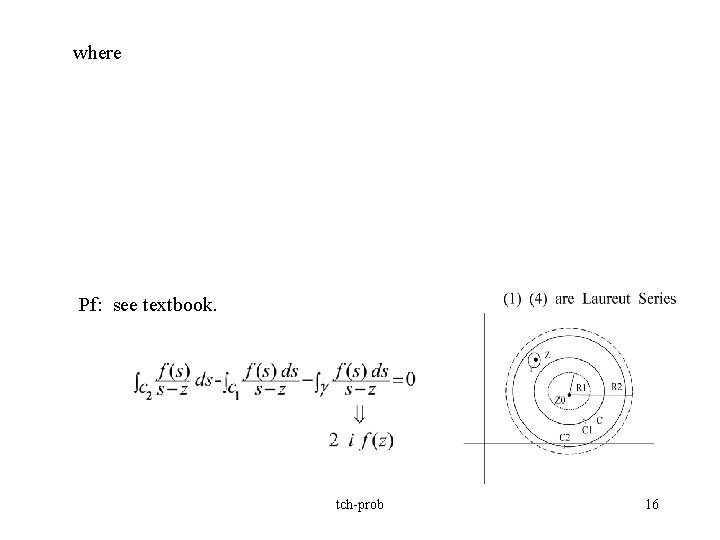
47. مثالها ضرایب در یک سری Laurent عموماً با روشی غیر از توسل مستقیم به نمایش انتگرال آنها یافت می شوند.  

مثال 2.

مثال 3. دارای دو نقطه مفرد z=1 و z=2 است و در حوزه ها تحلیلی است به یاد بیاورید که 

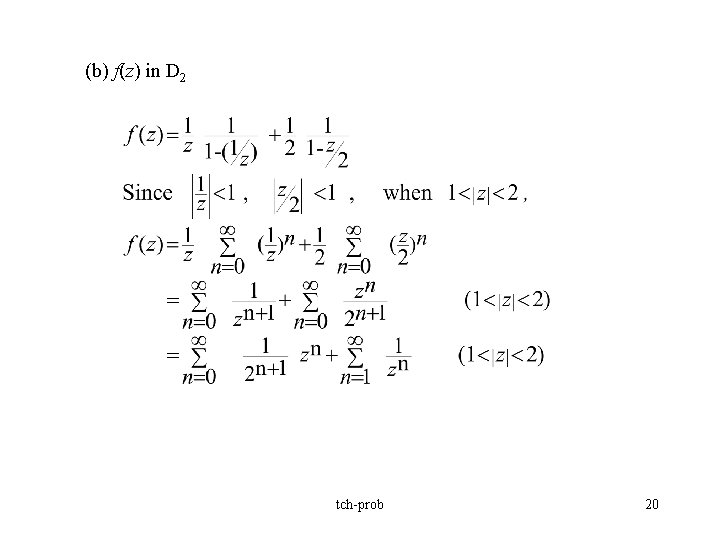
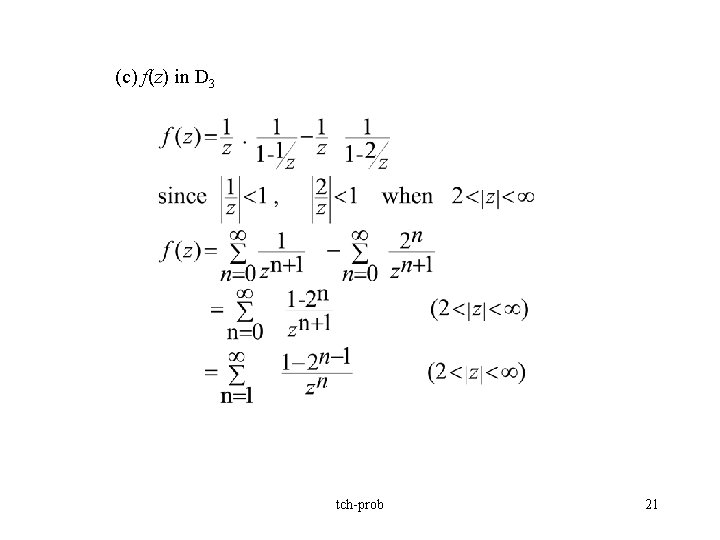
48. همگرایی مطلق و یکنواخت سری توانی 

• بزرگترین دایره با مرکز z 0 به طوری که سری (1) در هر نقطه از داخل همگرا شود دایره همگرایی سری (1) نامیده می شود. • طبق قضیه، سری نمی تواند در هر نقطه z 2 خارج از آن دایره همگرا شود. در غیر این صورت دایره همگرایی بزرگتر است. 

هنگامی که انتخاب فقط به مقدار و مستقل از نقطه z گرفته شده در یک منطقه مشخص در دایره همگرایی بستگی دارد، گفته می شود که همگرایی در آن ناحیه یکنواخت است. 

سپس آن سری به طور یکنواخت در نتیجه دیسک بسته همگرا است. 

49. یکپارچه سازی و تمایز سری های توانی اخیراً دیده شده است که یک سری توانی تابع پیوسته را در هر نقطه در داخل دایره همگرایی آن نشان می دهد. در این بخش بیان می کنیم که مجموع S(z) در واقع در دایره تحلیلی است. Thm 1. فرض کنید C نشان دهنده هر کانتور داخلی دایره همگرایی سری توان (1) باشد، و فرض کنید g(z) هر تابعی باشد که در C پیوسته است. سری ای که از ضرب هر جمله سری توان در g تشکیل می شود. (ز) را می توان ترم به ترم بر C ادغام کرد.

نتیجه. مجموع S(z) سری توانی (1) در هر نقطه z درون دایره همگرایی آن سری تحلیلی است. مثال 1. کامل است اما سری (4) به وضوح به f(0) همگرا می شود که z=0 باشد. بنابراین f(z) یک تابع کامل است.

. سری توان (1) را می توان ترم به ترم متمایز کرد. یعنی در هر نقطه z داخل دایره همگرایی آن سری، 

50. منحصر به فرد بودن نمایش سری Thm 1. اگر یک سری در همه نقاط داخل یک دایره باشد، آنگاه بسط سری تیلور برای f در توان های آن است. Thm 2. اگر یک سری به f(z) در تمام نقاط یک حوزه حلقوی حدود z 0 همگرا شود، آنگاه بسط سری Laurent برای f در توان آن دامنه است. 

51. ضرب و تقسیم سری توان فرض کنید که f(z) و g(z) توابع تحلیلی هستند در حاصلضرب آنها یک بسط سری تیلور  دارد.

منبع

http://www.nabla.hr/CL-PowerSeries5.htm