مثال 4 - برش شاخه [ ویرایش ]

انتگرال حقیقی را در نظر بگیرید

 

{\displaystyle \int _{0}^{\infty }{\frac {\sqrt {x}}{x^{2}+6x+8}}\,dx.}

 

می توانیم با فرمول بندی انتگرال مختلط شروع کنیم

 

{\displaystyle \int _{C}{\frac {\sqrt {z}}{z^{2}+6z+8}}\,dz=I.}

 

سوراخ کلید contour.svg

می‌توانیم دوباره از فرمول انتگرال کوشی یا قضیه باقیمانده برای بدست آوردن باقیمانده‌های مربوطه استفاده کنیم. با این حال، نکته مهمی که باید به آن توجه کنید این است که z 1/2 = e (Log z )/2 ، بنابراین z 1/2 دارای یک برش شاخه است. این بر انتخاب کانتور C ما تأثیر می گذارد . معمولاً برش شاخه لگاریتمی به عنوان محور حقیقی منفی تعریف می شود، با این حال، این محاسبه انتگرال را کمی پیچیده تر می کند، بنابراین ما آن را به عنوان محور حقیقی مثبت تعریف می کنیم.

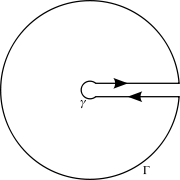
سپس، از کانتور سوراخ کلید استفاده می کنیم ، که شامل یک دایره کوچک در مورد مبدا شعاع ε است، که به یک پاره خط موازی و نزدیک به محور حقیقی مثبت امتداد می یابد، اما آن را لمس نمی کند، به یک دایره تقریباً کامل باز می گردد. به یک پاره خط موازی، نزدیک و زیر محور حقیقی مثبت به معنای منفی، بازگشت به دایره کوچک در وسط.

توجه داشته باشید که z = -2 و z = -4 داخل دایره بزرگ هستند. این دو قطب باقیمانده هستند که با فاکتورگیری مخرج انتگرال قابل استخراج هستند. نقطه انشعاب در z = 0 با انحراف در اطراف مبدا اجتناب شد.

 

فرض کنید γ دایره کوچک شعاع ε باشد ، Γ بزرگتر، با شعاع R ، سپس

 

{\displaystyle \int _{C}=\int _{\varepsilon }^{R}+\int _{\Gamma }+\int _{R}^{\varepsilon }+\int _{\gamma }. }

 

می توان نشان داد که انتگرال های روی Γ و γ هر دو به صورت ε → 0 و R → ∞ به صفر تمایل دارند ، با آرگومان تخمینی در بالا، که دو جمله باقی می گذارد. اکنون از آنجایی که z 1/2 = e (Log z )/2 ، در کانتور خارج از برش شاخه، 2 π را در آرگومان در امتداد γ به دست آورده‌ایم . (با هویت اویلر ، e i π نشان دهنده بردار واحد است، بنابراین π به عنوان log آن است. این π همان چیزی است که از آرگومان z استفاده می شود. ضریب1/2ما را مجبور می کند از 2 π استفاده کنیم .) بنابراین

 

{\displaystyle {\begin{aligned}\int _{R}^{\varepsilon }{\frac {\sqrt {z}}{z^{2}+6z+8}}\,dz&=\int _{ R}^{\varepsilon }{\frac {e^{{\frac {1}{2}}\operatorname {Log} z}}{z^{2}+6z+8}}\,dz\\[ 6pt]&=\int _{R}^{\varepsilon }{\frac {e^{{\frac {1}{2}}(\log |z|+i\arg {z})}}{z ^{2}+6z+8}}\,dz\\[6pt]&=\int _{R}^{\varepsilon }{\frac {e^{{\frac {1}{2}}\log |z|}e^{{\frac {1}{2}}(2\pi i)}}{z^{2}+6z+8}}\,dz\\[6pt]&=\int _ {R}^{\varepsilon }{\frac {e^{{\frac {1}{2}}\log |z|}e^{\pi i}}{z^{2}+6z+8} }\,dz\\[6pt]&=\int _{R}^{\varepsilon }{\frac {-{\sqrt {z}}}{z^{2}+6z+8}}\,dz \\[6pt]&=\int _{\varepsilon }^{R}{\frac {\sqrt {z}}{z^{2}+6z+8}}\,dz.\end{تراز شده}} }

 

از این رو:

 

{\displaystyle \int _{C}{\frac {\sqrt {z}}{z^{2}+6z+8}}\,dz=2\int _{0}^{\infty }{\frac {\sqrt {x}}{x^{2}+6x+8}}\,dx.}

 

با استفاده از قضیه باقیمانده یا فرمول انتگرال کوشی (ابتدا با استفاده از روش کسر جزئی برای به دست آوردن مجموع دو انتگرال خطوط ساده) به دست می آید.

 

{\displaystyle \pi i\left({\frac {i}{\sqrt {2}}}-i\right)=\int _{0}^{\infty }{\frac {\sqrt {x}} {x^{2}+6x+8}}\,dx=\pi \left(1-{\frac {1}{\sqrt {2}}}\right).\quad \square }