مثال 2 - توزیع کوشی [ ویرایش ]

انتگرال

{\displaystyle \int _{-\infty }^{\infty }{\frac {e^{itx}}{x^{2}+1}}\,dx}

 

کانتور

(که در نظریه احتمال به عنوان مضرب مقیاسی از تابع مشخصه توزیع کوشی به وجود می آید ) در برابر تکنیک های حساب ابتدایی مقاومت می کند . ما آن را با بیان آن به عنوان حدی از انتگرال های کانتور در امتداد خط C که در امتداد خط حقیقی از - a به a و سپس در خلاف جهت عقربه های ساعت در امتداد یک نیم دایره با مرکز 0 از a به - a می رود، ارزیابی می کنیم . a را بزرگتر از 1 در نظر بگیرید، به طوری که واحد خیالی i در داخل منحنی محصور شود. انتگرال کانتور است

 

{\displaystyle \int _{C}{\frac {e^{itz}}{z^{2}+1}}\,dz.}

 

از آنجایی که e itz یک تابع کامل است ( در هیچ نقطه ای از صفحه مختلط هیچ تکینگی ندارد)، این تابع فقط در جایی تکینگی دارد که مخرج z 2 + 1 صفر باشد. از آنجایی که z 2 + 1 = ( z + i ) ( z − i ) , این فقط در جایی اتفاق می افتد که z = i یا z = − i . تنها یکی از آن نقاط در منطقه ای است که توسط این کانتور محدود شده است. باقیمانده f ( z ) در z _ _= من هستم

 

{\displaystyle \lim _{z\to i}(zi)f(z)=\lim _{z\to i}(zi){\frac {e^{itz}}{z^{2}+1 }}=\lim _{z\to i}(zi){\frac {e^{itz}}{(zi)(z+i)}}=\lim _{z\to i}{\frac { e^{itz}}{z+i}}={\frac {e^{-t}}{2i}}.}

 

پس با توجه به قضیه باقی مانده ، داریم

 

{\displaystyle \int _{C}f(z)\,dz=2\pi i\operatorname {Res} _{z=i}f(z)=2\pi i{\frac {e^{-t }}{2i}}=\pi e^{-t}.}

 

کانتور C ممکن است به یک قسمت "مستقیم" و یک قوس منحنی تقسیم شود، به طوری که

 

{\displaystyle \int _{\text{straight}}+\int _{\text{arc}}=\pi e^{-t}،}

و بنابراین

 

{\displaystyle \int _{-a}^{a}=\pi e^{-t}-\int _{\text{arc}}.}

 

با توجه به لم جردن ، اگر t > 0 باشد

 

{\displaystyle \int _{\text{arc}}{\frac {e^{itz}}{z^{2}+1}}\,dz\rightarrow 0{\mbox{ as }}a\rightarrow \ نازک .}

 

بنابراین، اگر t > 0 باشد

 

{\displaystyle \int _{-\infty }^{\infty }{\frac {e^{itx}}{x^{2}+1}}\,dx=\pi e^{-t}.}

 

یک آرگومان مشابه با کمانی که به جای i به دور - i می پیچد، نشان می دهد که اگر t < 0 باشد

 

{\displaystyle \int _{-\infty }^{\infty }{\frac {e^{itx}}{x^{2}+1}}\,dx=\pi e^{t},}

و در نهایت این را داریم:

 

{\displaystyle \int _{-\infty }^{\infty }{\frac {e^{itx}}{x^{2}+1}}\,dx=\pi e^{-|t|} .\quad \square }

 

(اگر t = 0 باشد، انتگرال بلافاصله به روش‌های محاسباتی با ارزش حقیقی می‌رسد و مقدار آن π است .)

 

مثال 3a - انتگرال های مثلثاتی، روش کلی [ ویرایش ]

روش فوق ممکن است برای تمام انتگرال های نوع اعمال شود

{\displaystyle \int _{0}^{2\pi }{\frac {P{\big (}\sin(t),\sin(2t),\ldots ,\cos(t),\cos(2t ),\ldots {\big )}}{Q{\big (}\sin(t),\sin(2t),\ldots ,\cos(t),\cos(2t),\ldots {\big) }}}\,dt}

 

که در آن P و Q چند جمله ای هستند، یعنی یک تابع گویا در شرایط مثلثاتی در حال انتگرال است. توجه داشته باشید که مرزهای انتگرال ممکن است مانند مثال قبلی π و - π یا هر جفت نقطه پایانی دیگری با فاصله 2 π باشند.

ترفند این است که از جایگزینی z = e it استفاده کنید که در آن dz = یعنی آن dt و از این رو

 

{\displaystyle {\frac {1}{iz}}\,dz=dt.}

 

این جایگزینی بازه [0, 2π] را به دایره واحد ترسیم می کند. علاوه بر این،

 

{\displaystyle \sin(kt)={\frac {e^{ikt}-e^{-ikt}}{2i}}={\frac {z^{k}-z^{-k}}{2i }}}

و

 

{\displaystyle \cos(kt)={\frac {e^{ikt}+e^{-ikt}}{2}}={\frac {z^{k}+z^{-k}}{2 }}}

به طوری که یک تابع منطقی f ( z ) در z از جایگزینی حاصل می شود و انتگرال تبدیل می شود

 

{\displaystyle \oint _{|z|=1}f(z){\frac {1}{iz}}\,dz}

که به نوبه خود با جمع کردن باقیمانده های f ( z ) محاسبه می شود.1/izداخل دایره واحد

 

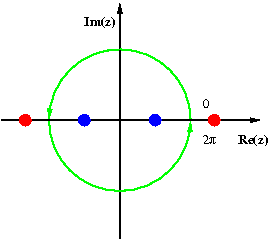
TrigonometricToComplex.png

تصویر سمت راست این موضوع را نشان می دهد

 

{\displaystyle I=\int _{0}^{\frac {\pi }{2}}{\frac {1}{1+(\sin t)^{2}}}\,dt,}

که اکنون محاسبه می کنیم. اولین قدم تشخیص آن است

 

{\displaystyle I={\frac {1}{4}}\int _{0}^{2\pi }{\frac {1}{1+(\sin t)^{2}}}\,dt .}

 

جایگزینی نتیجه می دهد

 

{\displaystyle {\frac {1}{4}}\oint _{|z|=1}{\frac {4iz}{z^{4}-6z^{2}+1}}\,dz=\ Oint _{|z|=1}{\frac {iz}{z^{4}-6z^{2}+1}}\,dz.}

 

قطب های این تابع در

 1 ± √ 2 

و 

−1 ± √ 2 

هستند. از این میان،

 1 + √ 2

 و 

−1 − √ 2 

خارج از دایره واحد (به رنگ قرمز نشان داده شده است، نه به مقیاس)، در حالی که 

1 − √ 2 

و 

−1 + √ 2 

در داخل دایره واحد هستند (به رنگ آبی نشان داده شده است). باقی مانده های مربوطه هر دو برابر با - هستند

i √ 2/16،

به طوری که مقدار انتگرال است

 

{\displaystyle I=2\pi i\;2\left(-{\frac {\sqrt {2}}{16}}i\right)=\pi {\frac {\sqrt {2}}{4} }.}