کلاین چهار گروه
این مقاله در مورد یک گروه خاص است ، یعنی یک گروه منحصر به فرد تا ایزومورفیسم . مشاهده اطلاعات خاص (مانند تئوری نمایش خطی، ساختار زیر گروه) در مورد این گروه
مشاهده لیست کاملی از گروه های خاص (این یک لیست بسیار بزرگ است!) [نمایش بیشتر]
فهرست
تعریف
تعاریف کلامی
چهار گروه کلاین که معمولاً نشان داده می شود 
، به روش های معادل زیر تعریف می شود:
- این است محصول مستقیم از گروه
با خود - این گروه شامل عناصر
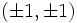تحت ضرب مختصات است - این گروه منحصر به فرد غیر چرخه ای از مرتبه 4 است
- این زیر گروه از گروه متقارن درجه چهار است که شامل جابجایی های دوگانه و عنصر هویت است.
- این گروه Burnside است
: گروه آزاد روی دو مولد با توان دو.
جدول ضرب
جدول ضرب با عناصر غیر هویت 
و عنصر هویت 
:
| عنصر/عنصر | |  |  |  |
|---|---|---|---|---|
| | | | |
| | | | |
| | | | |
| | | | |
جدول ضرب را می توان به صورت زیر توصیف کرد (و این گروه را مشخص می کند):
- محصول عنصر هویت و هر عنصری خود آن عنصر است.
- محصول هر عنصر غیر هویتی با خود عنصر هویت است.
- حاصلضرب دو عنصر غیر هویتی متمایز، سومین عنصر غیر هویتی است.
عناصر
اطلاعات بیشتر: ساختار عناصر گروه چهارگانه کلاین
تا صرف
چهار کلاس conjugacy وجود دارد که هر کدام شامل یک عنصر است (کلاس های conjugacy تک تن هستند زیرا گروه abelian هستند .
تا اتومورفیسم
دو طبقه هم ارزی از عناصر تا اتومورفیسم وجود دارد: عنصر هویت به صورت تکی و همه عناصر غیر هویت. همه عناصر غیر هویتی در خودمورفیسم معادل هستند.
توابع حسابی
آیا می خواهید به مقایسه و کنتراست مقادیر تابع ریاضی با گروه های دیگر از همان سفارش ؟ اتمام گروه از سفارش 4 # توابع ریاضی
خواص گروهی
| ویژگی | راضی؟ | توضیح | اظهار نظر |
|---|---|---|---|
| گروه آبلیان | آره | ||
| گروه Nilpotent | آره | ||
| گروه آبلیان ابتدایی | آره | ||
| گروه قابل حل | آره | ||
| گروه فوق حل شدنی | آره | ||
| گروه چرخه ای | خیر | ||
| گروه منطقی-بازنمایی | آره | ||
| گروه منطقی | آره | ||
| گروه دوسوگرا | آره |
اندومورفیسم ها
اتومورفیسم ها
گروه اتومورفیسم به طور طبیعی با گروه 
به شرح زیر شناخته می شود. هر عنصر از گروه اتومورفیسم مربوط به جایگشتی از سه عنصر غیر هویتی است.
holomorph ، یعنی کالا مستقیم با گروه automorphism ، است گروه متقارن در 4 عناصر .
اندومورفیسم ها
اندومورفیسم های غیر اتومورفیسم عبارتند از:
- نقشه بی اهمیت
- یک تجزیه مجموع مستقیم دلخواه و یک زیرگروه دو عنصری دلخواه را انتخاب کنید. سپس پیش بینی اولین عامل مستقیم برای تجزیه، که با ایزومورفیسم به زیرگروه دو عنصری دیگر تشکیل شده است، یک اندومورفیسم است.
زیر گروه ها
اطلاعات بیشتر: ساختار زیر گروهی کلاین چهار گروهی
خلاصه سریع
| مورد | مقدار |
|---|---|
| تعداد زیر گروه ها | 5 به عنوان گروه آبلی ابتدایی از ترتیب مربع اول برای اول  : |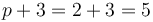
| تعداد کلاس های مزدوج زیر گروه ها | 5 (همان تعداد زیر گروه ها، زیرا گروه یک گروه آبلی است |
| تعداد طبقات اتومورفیسم زیر گروه ها | 3 به عنوان گروه آبلی ابتدایی از سفارش  : |
| طبقات ایزومورفیسم زیر گروه ها | گروه چیزهای بی اهمیت (1 بار)، گروه چرخه ای: Z2 (3 بار، همه در یک کلاس اتومورفیسم)، کلاین چهار گروه (1 بار). |
جدول طبقه بندی زیر گروه ها تا اتومورفیسم
توجه داشته باشید که چون abelian به معنای عادی بودن هر زیرگروه است ، همه زیرگروه ها زیرگروه های عادی هستند .
| کلاس اتومورفیسم از زیر گروه ها | لیست زیر گروه ها | کلاس ایزومورفیسم | ترتیب زیر گروه ها | فهرست زیر گروه ها | تعداد کلاس‌های مزدوج (=1 زیرگروه automorph-conjugate ) | اندازه هر کلاس مزدوج (=1 اگر زیرگروه عادی ) | تعداد کل زیر گروه ها (=1 زیرگروه مشخصه اگر ) | کلاس ضریب ایزومورفیسم (در صورت وجود) | عمق غیر طبیعی | کلاس Nilpotency |
|---|---|---|---|---|---|---|---|---|---|---|
| زیر گروه بی اهمیت |  | گروه بی اهمیت | 1 | 4 | 1 | 1 | 1 | کلاین چهار گروه | 1 | 0 |
| Z2 در V4 |  | گروه چرخه ای: Z2 | 2 | 2 | 3 | 1 | 3 | گروه چرخه ای: Z2 | 1 | 1 |
| کل گروه |  | کلاین چهار گروه | 4 | 1 | 1 | 1 | 1 | گروه بی اهمیت | 0 | 1 |
| مجموع (3 ردیف) | -- | -- | -- | -- | 5 | -- | 5 | -- | -- | -- |
گروه های بزرگتر
گروه های حاوی آن به عنوان یک زیر گروه
- گروه متناوب: A4 که محصول نیمه مستقیم گروه کلاین-فور توسط یک گروه چرخه ای از مرتبه 3 است.
- گروه متقارن: S4 که هولومورف گروه کلاین-فور است و در آن گروه کلاین-فور یک زیر گروه مشخصه است.
- گروه دو وجهی : D8 که گروه دو وجهی مرتبه 8 است که بر روی مجموعه ای از چهار عنصر عمل می کند. بین گروه کلاین-فور و گروه متقارن روی 4 عنصر قرار دارد
توجه داشته باشید که گروه کلاین-فور به دو صورت در داخل گروه متقارن قرار می گیرد، یکی به صورت جابجایی دوگانه و دیگری به عنوان حاصلضرب مستقیم یک جفت چرخش. ما معمولاً به تعبیه قبلی اشاره می کنیم، زمانی که هیچ چیزی به صراحت بیان نشده است.
گروه هایی که آن را به عنوان ضریب دارند
به طور کلی، هر گاه گروهی زیر گروهی از شاخص دو داشته باشد که مشخصه نباشد ، محل تلاقی آن زیر گروه و هر اتومورف دیگری از آن، شاخص چهار است و ضریب به دست آمده، گروه کلاین-فور است.
همچنین ممکن است به عنوان تقاطع شاخص - دو زیر گروه که خودمورف یکدیگر نیستند رخ دهد.
چند نمونه:
- گروه چهارگانه ، که دارای گروه کلاین و چهار عنوان آن گروه automorphism داخلی . زیرگروه های نرمال را می توان به عنوان زیرگروه هایی در نظر گرفت که توسط ریشه های مربع ایجاد می شوند
- گروه دوسطحی از سفارش هشت ، که دارای گروه کلاین و چهار عنوان آن گروه automorphism داخلی . در اینجا، ضریب تقاطع دو زیر گروه از مرتبه چهار است، که یکی زیرگروه چرخه‌ای است و دیگری خود یک گروه کلاین-فور است.
پیاده سازی در GAP
شناسه گروه
این گروه محدود دارای مرتبه 4 و دارای شناسه 2 در میان گروه های مرتبه 4 در کتابخانه SmallGroup GAP است. برای زمینه، گروه هایی از مرتبه 4 وجود دارد. بنابراین می توان آن را با استفاده از تابع SmallGroup GAP به صورت زیر تعریف کرد :
SmallGroup (4،2)
برای مثال، می‌توانیم از تخصیص زیر در GAP برای ایجاد گروه و نامگذاری آن استفاده کنیم 
:
gap> G := SmallGroup(4,2);
برعکس، برای بررسی اینکه آیا یک گروه معین در واقع همان گروهی است که می خواهیم، می توانیم از تابع IdGroup GAP استفاده کنیم:
IdGroup(G) = [4,2]
یا فقط انجام دهید:
IdGroup(G)
برای داشتن خروجی GAP شناسه گروه، که سپس می توانیم آن را با آنچه می خواهیم مقایسه کنیم.
توضیحات دیگر
این گروه همچنین می تواند با استفاده از تابع ElementaryAbelianGroup GAP به صورت زیر تعریف شود :
ElementaryAbelianGroup (4)
در این وبلاگ به ریاضیات و کاربردهای آن و تحقیقات در آنها پرداخته می شود. مطالب در این وبلاگ ترجمه سطحی و اولیه است و کامل نیست.در صورتی سوال یا نظری در زمینه ریاضیات دارید مطرح نمایید .در صورت امکان به آن می پردازم. من دوست دارم برای یافتن پاسخ به سوالات و حل پروژه های علمی با دیگران همکاری نمایم.در صورتی که شما هم بامن هم عقیده هستید با من تماس بگیرید.