ریاضیات

 
از ویکیپدیا، دانشنامه آزاد

در ریاضیات ، به ویژه در حوزه جبر انتزاعی که به عنوان نظریه مدول شناخته می شود ، یک مدول انژکتیو یک مدول Q است که ویژگی های مطلوب خاصی را با مدول Z - Q از همه اعداد گویا به اشتراک می گذارد . به طور خاص،اگر Q است زیرمدول برخی از مدول های دیگر، سپس آن را در حال حاضر یک جمع وند مستقیم که مدول. همچنین، با توجه به زیرمدول یک مدول Y ، آنگاه هر هم شکلی مدول از این زیرمدول به Q را می توان به یک هم شکلی از همه Y گسترش داد.به س . این مفهوم دوگان به مفهوم مدول های تصویری است . مدول های انژکتیو در ( بئر 1940 ) معرفی شدند و در کتاب درسی با جزئیات مورد بحث قرار گرفته اند ( لم 1999 ، §3).

مدول‌های انژکتیو به‌شدت مورد مطالعه قرار گرفته‌اند، و انواع مفاهیم اضافی بر اساس آنها تعریف شده‌اند: هم مولدهای انژکتیو، مدول‌های انژکتیو هستند که به طور صادقانه کل دسته مدول‌ها را نشان می‌دهند. تفکیک‌پذیری‌های انژکتیو اندازه‌گیری می‌کنند که یک مدول از نظر ابعاد انژکتیو چقدر فاصله دارد و مدول‌ها را در دسته مشتق شده نشان می‌دهد . بدنه های انژکتیو حداکثر پسوندهای ضروری هستند و ظاهراً حداقل پسوند انژکتیو هستند. بر روی یک حلقه نوتر ، هر مدول انژکتیو به طور منحصر به فرد یک مجموع مستقیم از تجزیه ناپذیر است.مدول ها و ساختار آنها به خوبی درک شده است. یک مدول انژکتیو روی یک حلقه، ممکن است روی حلقه دیگر انژکتیو نباشد، اما روش‌های کاملاً درک شده‌ای برای تغییر حلقه‌ها وجود دارد که موارد خاص را مدیریت می‌کند. حلقه‌هایی که خود مدول‌های انژکتیو هستند دارای تعدادی ویژگی جالب هستند و شامل حلقه‌هایی مانند حلقه‌های گروهی از گروه‌های متناهی بر روی میدان‌ها می‌شوند . مدول های انژکتیو شامل گروه های قابل تقسیم هستند و با مفهوم اشیاء انژکتیو در نظریه رسته تعمیم می یابند .

فهرست

• 1تعریف
• 2مثال ها
  • 2.1اولین نمونه ها
  • 2.2مثال های جابجایی
  • 2.3نمونه های آرتینی
    • 2.3.1محاسبات بدنه انژکتیو
    • 2.3.2خود انژکتیو
  • 2.4مدول ها بر روی جبرهای دروغ
• 3تئوری
  • 3.1قضیه ساختار برای حلقه های نوترین جابجایی
  • 3.2زیر مدول ها، ضرایب، محصولات و مجموع
  • 3.3معیار بائر
  • 3.4کو مولدهای انژکتیو
  • 3.5بدنه انژکتیو
  • 3.6قطعنامه های انژکتیو
  • 3.7تجزیه ناپذیر
  • 3.8تغییر حلقه ها
  • 3.9حلقه های خود انژکتیو
• 4تعمیم و تخصص
  • 4.1اشیاء انژکتیو
  • 4.2گروه های قابل تقسیم
  • 4.3تزریقات خالص
• 5منابع
  • 5.1یادداشت
  • 5.2کتاب های درسی
  • 5.3منابع اولیه

تعریف [ ویرایش ]

یک مدول سمت چپ Q بر روی حلقه R در صورتی انژکتیو است که یکی (و بنابراین همه) از شرایط معادل زیر را برآورده کند:

• اگر Q زیرمدول ب سمت چپ  R -مدول M است ، پس یکی دیگر  زیرمدول وجود دارد K از M به طوری که M است مجموع مستقیم داخلی از Q و K ، یعنی Q + K = M و Q ∩ K = {0}.
• هر دنباله دقیق کوتاه  

0→Q → M → K → 0

ازR مدول   سمت چپ های شکافته می شود .

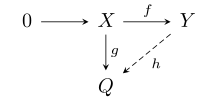
• اگر X و Y از مدول‌های R باقی مانده باشند، f  : X → Y یک هم‌ریختی مدول بک به یک است و g  : X → Q یک همریختی مدول دلخواه است، در این صورت یک همریختی مدول وجود دارد h  : Y → Q به طوری که hf = g ، یعنی به طوری که در نمودار زیر جابجایی باشد:

​

​