ریاضیات

اگر هدف ما یافتن تعمیم نسبیتی معادله پواسون برای میدان گرانشی است:

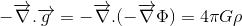
جایی که Φ به پتانسیل گرانشی و ρ به چگالی جرم اشاره دارد، ما در نیمه راه هستیم.

در واقع، قبلاً در مقاله قبلی تانسور انرژی- تکانه دیده بودیم که تعمیم چگالی جرم (جمله سمت راست معادله) با انرژی-تکانه T μν مطابقت دارد .

بنابراین منطقی به نظر می رسد که فرض کنیم معادله ما باید به شکل زیر باشد:

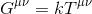
که در آن k مخفف یک اسکالر است و G μν ، که تانسور انیشتین نامیده می شود ، نشان دهنده تانسور رتبه-2 است که انحنای فضازمان را توصیف می کند.

تا آنجا که می دانیم، G μν باید از محدودیت های زیر تبعیت کند:

- باید در فضازمان مسطح باطل شود

- باید انحنای فضازمان را توصیف کند و با توجه به تانسور ریمان خطی باشد

- باید متقارن و دارای رتبه 2 باشد (به عنوان T μν )

- باید واگرایی صفر داشته باشد (به عنوان T μν )

- و در نهایت در حدود نیوتنی باید به 4πGρ کاهش یابد

اولین تلاش با تانسور Ricci به عنوان راه حل

ما از مقاله ما یاد معادله ژئودزیک در نیوتنی حد که Φ پتانسیل گرانشی به 00 جزء از متریک از طریق ساعت مرتبط 00 = (گرم 00 -1) / ج 2

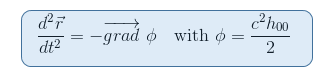
بنابراین طبیعی به نظر می رسد که به دنبال تانسوری بگردیم که مشتقات دوم متریک را در بر می گیرد ، که این مورد برای تانسور ریمان است . علاوه بر این، تانسور ریمان تنها کاندیدایی است که تاکنون می‌دانیم قادر به توصیف انحنای فضازمان است (قید دوم در بالا).

از آنجایی که ما باید یک تانسور رتبه-2 را پیدا کنیم، و اگر فرض کنیم که باید راه حلی را صرفاً بر اساس تانسور ریمان پیدا کنیم، طبیعی به نظر می رسد که ابتدا شکل منقبض تانسور ریمان را در نظر بگیریم که به تانسور ریچی معروف است [ 1] .

برای مشاهده این موضوع، اجازه دهید بیان تانسور ریمان را از مقاله تانسور انحنای ریمان قسمت دوم: اشتقاق از انحراف ژئودزیکی به یاد آوریم.

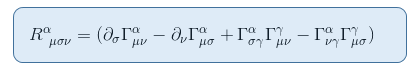
 در محدوده میدان گرانشی ایستا و ضعیف، فقط یک جمله به R 00 کمک می کند :

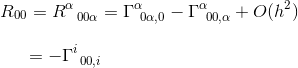
در همین مقاله این نماد کریستوفل را محاسبه کرده ایم و متوجه شده ایم

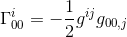
 با تقریب g ij = η ij   و g oo,j = h oo,j (به مقاله مراجعه کنید) بدست می آوریم:

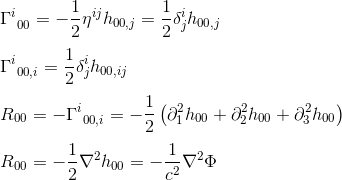
شناسایی R 00 با ΔΦ (عملگر لاپلاس) نشان می دهد که معادله میدان در نسبیت عام باید R برابر AB به مضربی ثابت T AB .

در سال 1915، با استفاده از این معادله، انیشتین حتی توانست مشکل طولانی مدت انقطاع حضیض عطارد را حل کند و باعث شد در نوامبر همان سال بنویسد: "چند روزی با هیجان شادی در کنار خودم بودم."

در نهایت، انیشتین مجبور شد این اولین تلاش را رد کند ، زیرا به طور کلی واگرایی R ab باطل نمی شود .

تلاش دوم

یک تانسور نزدیک به اسکالر ریچی وجود دارد که می توان آن را بدون تناقض در سمت چپ قرار داد. این تانسور انیشتین را به صورت زیر تعریف می کند:

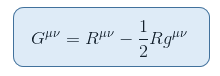
که در آن R = R است اسکالر ریچی یا انحنای اسکالر .

این شکل از G ab متقارن و در رتبه 2 است و به وضوح انحنای فضازمان را توصیف می کند. بنابراین فقط باید نشان دهیم که مشتق کل صفر است

برای انجام این کار، با هویت The Bianchi شروع می کنیم

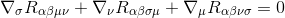
با ضرب در g γσ g am g βν (مشتقات متریک صفر هستند، بنابراین آنها به عنوان ثابت عمل می کنند و می توانند در مشتقات گرفته شوند)، نتیجه می شود:

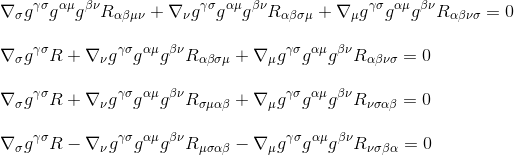
با استفاده از تعریف تانسور ریچی R μν =g μβ g νσ R βσ (مرحله 3) و با تغییر نام شاخص ها (مرحله 4)، به دست می آوریم.

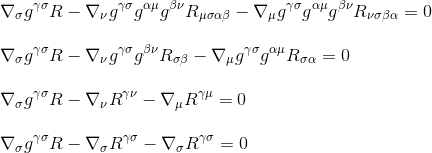
با فاکتورسازی مشتق، در نهایت به دست می آوریم

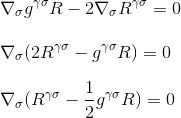
که دقیقاً همان چیزی است که می‌خواستیم نشان دهیم: واگرایی تانسور اینشتین صفر است، و ما نامزد مناسب را برای سمت چپ معادله انحنای/جرم-انرژی خود پیدا کرده‌ایم.

[1] اینشتین و گروسمن قبلاً تانسور ریچی را به عنوان یک نامزد بالقوه برای تانسور گرانشی در سال 1913 پیشنهاد کرده بودند، اما به دلایل اشتباه آن را رد کردند. برای جزئیات بیشتر به مقاله 1913 Entwurf یا فرصت از دست رفته مراجعه کنید

منبع

https://einsteinrelativelyeasy.com/index.php/general-relativity/80-einstein-s-equations