ریاضیات

در دو مقاله قبلی خود، بیان نسبتاً پیچیده تانسور انحنای ریمان را استنباط کردیم، مخلوطی باشکوه از مشتقات و محصولات ضرایب اتصال، با 256 (=4^4) جزء در فضازمان چهار بعدی.

اما ما همچنین در مقاله خود مسطح بودن محلی یا قاب‌های اینرسی محلی و انحنای SpaceTime نشان داده‌ایم که هر سیستم مختصات دلخواه می‌تواند تمام مشتقات به جز 20 ثانیه یک متریک معین را در یک فضازمان منحنی باطل کند . هدف ما در این مقاله نشان دادن این است که تانسور ریمان تنها 20 جزء مستقل دارد و این مؤلفه دقیقاً ترکیبی از این مشتقات ثانویه و نه تهی هستند.

روشی که در آنجا اتخاذ می شود مطالعه تقارن های تانسور ریمان   در یک قاب اینرسی محلی (LIF) است - همانطور که می دانیم همه نمادهای کریستوفل تهی هستند - و تعمیم این تقارن ها به هر قاب مرجع، همانطور که طبق تعریف یک معادله تانسور معتبر در یک ارجاع داده شده در هر چارچوب ارجاعی دیگری صادق خواهد بود.

تقارن تانسور ریمان

اجزای مستقل تانسور ریمان

با استفاده از تعریف تانسور ریمان همانطور که در مقالات قبلی دیده می شود:

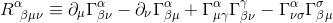
و با دانستن اینکه تمام نمادهای کریستوفل در مبدا Local Inertial Frame تهی هستند، این عبارت به صورت زیر ساده می شود:

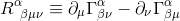
با اعمال مکانیسم انقباض همانطور که در مقدمه تانسورها نشان داده شده است ، می‌توانیم تانسور ریمان را با همه شاخص‌ها بازنویسی کنیم:

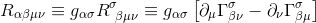
ما از مقاله خود نمادهای کریستوفل را از نظر تانسور متریک به یاد داریم که چگونه نماد کریستوفل را با توجه به مشتقات متریک بنویسیم:

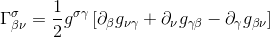
تا بتوانیم بنویسیم

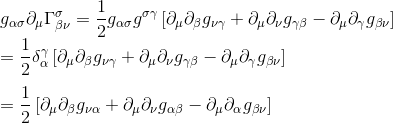
با جایگزینی شاخص های μ و ν، جمله دوم عبارت تانسور ریمان را به دست می آوریم:

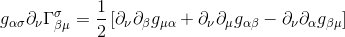
با تفریق این دو عبارت، می بینیم که عبارت های میانی لغو می شوند، بنابراین ما با آن روبرو می شویم:

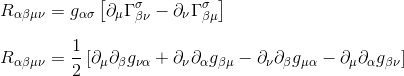
واضح است که این را می توان به صورت زیر نوشت:

به خاطر داشته باشید که این معادله فقط در مبدأ یک LIF معتبر است . با این حال، منشأ یک LIF یک رویداد خاص را در فضازمان تعریف می‌کند و از آنجایی که همه این تقارن‌ها معادلات تانسوری هستند ، صرف نظر از اینکه از کدام سیستم مختصاتی استفاده می‌کنیم ، باید برای آن رویداد خاص صادق باشند .

به همین ترتیب، می‌توانیم به راحتی نشان دهیم که تانسور ریمان تحت مبادله دو شاخص اول خود متقارن است:

اگر شاخص های اول و سوم (α <-> μ) و همچنین دوم و چهارم (β <-> ν) را با هم عوض کنیم، به دست می آید:

خاصیت تقارن نهایی کمی ظریف تر است. اگر 3 شاخص آخر β، μ و ν را به صورت چرخه ای جایگذاشته و 3 جمله را جمع کنیم، به دست می آید.

منبع

https://einsteinrelativelyeasy.com/index.php/general-relativity/66-riemann-tensor-3