ریاضیات

ر این مقاله تانسور متریک اقلیدسی برای سطح یک کره در مختصات کروی را به دو صورت محاسبه می کنیم، همانطور که در مقاله قبلی مشاهده شد تعمیم تانسور متریک.

• - با استنتاج متریک مستقیماً از عنصر خط فاصله
• - با محاسبه متریک از حاصل ضرب مشتقات سیستم مختصات دکارتی دو بعدی

مختصات کروی (r، θ، φ) که معمولاً در فیزیک استفاده می‌شود: فاصله شعاعی r، زاویه قطبی θ (تتا)، و زاویه‌ای ازیموتال φ (ph). منبع ویکی پدیا

استنتاج متریک توسط عنصر خط

در این فضای سه بعدی اقلیدسی، عنصر خط توسط:

dl 2 = dr 2 + r 2 dθ 2 + r 2 sin 2 θdΦ 2

اگر مختصات قطبی r را مقداری ثابت R قرار دهیم، عبارت dr را از دست می دهیم (زیرا r اکنون ثابت است) و عنصر خط اکنون تبدیل می شود: 

dl 2 = R 2 dθ 2 + R 2 sin 2 θdΦ 2

که یک سطح دو بعدی را با استفاده از دو مختصات قطبی (θ, Φ) توصیف می کند.

یا از مقاله قبلی می دانیم که این عنصر خط را می توان به صورت زیر نوشت:

dl 2 = g ij dx i dy j

ما می توانیم بلافاصله استنباط کنیم که متریک و معکوس متریک برای این سطح، با استفاده از مختصات x 0 =θ و x 1 =Φ، عبارتند از:

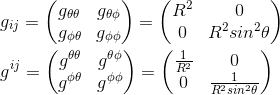
این قسمت آسان بود بیایید سعی کنیم همان متریک را با استفاده از فرمول حاصل ضرب مشتقات مختصات محاسبه کنیم.

محاسبه متریک توسط حاصل ضرب مشتقات مختصات دکارتی

باید به خاطر داشته باشیم که ما تانسور متریک را نیز به عنوان حاصل ضرب مشتقات به یک سیستم مختصات دیگر تعریف کردیم (در مقاله قبلی، از یک مرجع اینرسی مینکوفسکی بود)

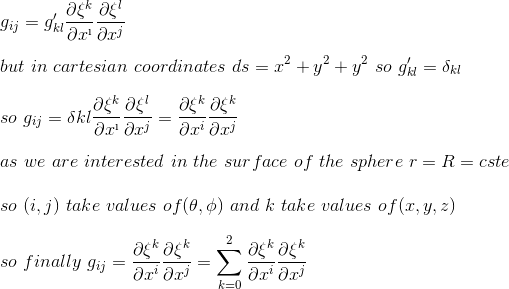
 یا مختصات دکارتی و مختصات کروی با معادلات زیر به هم مرتبط می شوند:

در این مرحله می‌توانیم تأیید کنیم که هم با عنصر خط فضا و هم با حاصل ضرب مشتقات مختصات، دقیقاً مؤلفه‌های مشابهی را برای متریک سطح دو بعدی یک کره در مختصات قطبی پیدا کرده‌ایم.

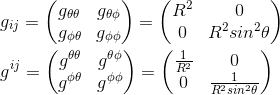
منبع

http://einsteinrelativelyeasy.com/index.php/general-relativity/35-metric-tensor-exercise-calculation-for-the-surface-of-a-sphere