حساب دیفرانسیل و انتگرال III:
انتگرال های خطی با توجه به طول قوس ds
1. تعریف و روش انتگرال یک تابع از یک متغیر منفرد f(x) در بازه [a,b]، x تمام مقادیر این بازه را می گیرد که از a شروع می شود و به b ختم می شود.
انتگرال دوگانه یک تابع از دو متغیر f(x,y) روی یک دامنه [a,b] D، x و y تمام مقادیر این دامنه را که از a شروع میشوند و به b ختم میشوند، برای x میگیرند. و شروع atc و ختم به d برای y.
با انتگرال های خطی ، تابع f(x,y)، تابعی از دو متغیر را انتگرال می کنیم، و مقادیر x و y نقاط (x,y) هستند که روی منحنی C قرار دارند .
توجه داشته باشید که این با انتگرال های دوگانه که در آن انتگرال بر روی یک منطقه R یا D انجام می شود متفاوت است. در انتگرال های خطی، ما روی یک منحنی ساخته شده از نقاط خود تابع انتگرال می کنیم.
بیایید منحنی C را که نقاط از آن آمده اند در نظر بگیریم و فرض کنیم منحنی صاف است. منحنی توسط معادلات پارامتری به دست می آید:
x = g(t)، y = h(t) a ≤ t ≤ b
با پارامتری شدن منحنی به عنوان یک تابع برداری، منحنی با: (t) = g( t) + h(t) a ≤ t ≤ b بیاد بیاوریم که منحنی صاف نامیده می شود اگر (t) پیوسته و (t) ≠ برای همه t باشد. انتگرال خط f(x,y) در امتداد C با: عنصر دیفرانسیل ds است. این واقعیتی است که ما در امتداد منحنی، C، به جای dx برای محور x، یا dy برای محور y، حرکت می کنیم. فرمول فوق را می نامند
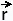 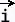 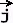
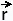 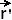 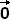
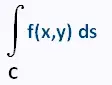
انتگرال خط f نسبت به طول قوس .
بیایید به یاد بیاوریم که طول قوس یک منحنی توسط معادلات پارامتری به دست میآید:
L = ∫ a b ds عرض ds = √[(dx/dt) 2 + (dy/dt) 2 ] dt
بنابراین، برای محاسبه یک انتگرال خطی ما همه چیز را به معادلات پارامتری تبدیل کنید. سپس انتگرال خط به صورت زیر است:
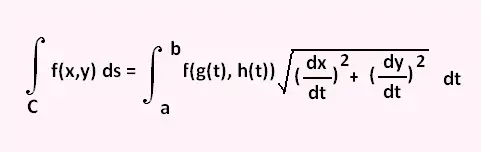 مثال 1 ∫ C 3x 2 ds را که در آن C پاره خط از (-1، 1) تا (1،2) است، ارزیابی کنید.
قبلاً در معادله یک خط در بخش فضای سه بعدی دیدیم که فرمول پارامترسازی پاره خطی که از نقطه (xo, yo) شروع می شود و به نقطه (x1,y1) ختم می شود: (t) = ( 1 - t) 〈xo, yo〉 + t 〈x1,x2〉 یعنی: x = xo (1 - t) + x1 t y = yo (1 - t) + y1 t بنابراین، فرمول پارامترسازی پاره خط از (-1، -1) شروع می شود و به (1،2) ختم می شود: (t) = (1 - t) 〈-1, 1〉 + t 〈1،2〉. یعنی: x = (1 - t) (- 1) + t(1) = 2t - 1 y = (1 - t) (1) + t(2) = t + 1 at (-1, 1): x = - 1، y = 1 → t = 0
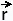

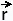
و
در (1,2): x = 1 , y = 2 → t = 1
پس 0 ≤ t ≤ 1
داریم: dx/dt = 2 و dy/dt = 1. از این رو:
ds = √[2 2 + 1 2 ] dt = √5 dt.
ds = √5 dt
بنابراین
∫ C 3x 2 ds = ∫ 0 1 3(2t - 1) 2 √5 dt = 3 √5 ∫ 0 1 (4t 2 - 4t + 1) dt =
3√5 [(4/3 )t 3 - 2t 2 + t] 0 1 = 3√5 [(4/3) - 2 + 1] =
3√5 [1/3] = √5
∫ C 3x 2 = √5 مثال 2 ∫ C xy 2 ds را در جایی که C نیمه سمت راست دایره x 2 + y 2 = 16 است که در خلاف جهت عقربه های ساعت چرخیده است، ارزیابی کنید.

منحنی را که دایره است، سپس انتگرال و سپس عنصر دیفرانسیل را پارامتر می کنیم:
x = 4 cos t، y = 4 sin t - π/2 ≤ t ≤ + π/2.
f(x,y) = xy 2 = 4 cos t (4 sint) 2 = 64 cos t sin 2 t
dx/dt = - 4 sin t , dy/dt = 4 cos t
ds = 4 dt
بنابراین
∫ C xy 2 ds = ∫ - π/2 + π/2 64 cos t sin 2t (4 dt) =
256 ∫ - π/2 + π/2 cos t sin 2 t dt = 256 [(1/3) sin 3 t] - π/2 + π/2 =
(256/3)[sin 3 (π/2) - sin 3 (-π/2)] = 2 (256/3) sin 3 (+ π/2) = 2 (256/3) = 512/3.
∫ C xy 2 ds = 512/3 2. انتگرال ها روی منحنی های صاف تکه ای 
اکنون میخواهیم انتگرالهای خط را روی منحنیهای صاف تکهای انتگرال کنیم .
منحنی صاف تکه ای C هر منحنی است که بتوان آن را به صورت اتحاد تعداد محدودی از منحنی های صاف نوشت، C1, C2, C3, , ... Cn که در آن نقطه پایان Ci نقطه شروع Ci+1 است.
برای ارزیابی انتگرال های خط روی منحنی های صاف تکه ای، انتگرال خط را روی هر یک از قطعات ارزیابی می کنیم و سپس آنها را جمع می کنیم:
∫ C f(x,y) ds = ∫ C1 f(x,y) ds ∫ C2 f(x ,y) ds ∫ C3 f(x,y) ds ∫ C4 f(x,y) ds ∫ C5 f(x,y) ds + ...
مثال 3 ∫ C 2x ds را
که در آن C منحنی زیر است، ارزیابی کنید.

C1: x = t، y = 3 - 4 ≤ t ≤ 0
C2: x = 3 cos t، y = 3 sin t π/2 ≤ t ≤ 0
C3: x = 3، y = t - 3 ≤ t ≤ 0
C1:
dx/dt = 1 dy/dt = 0
ds = dt
∫ C1 2x ds = ∫ - 4 0 2t dt = (t 2 )| - 4 0 = 16
∫ C1 2x ds = 16
C2:
dx/dt = - 3 sint dy/dt = 3 coos t
ds = 3 dt
∫ C2 2x ds = ∫ π/2 0 2 cos t (3 dt) = 6 (سین ت)| π/20 = 6 (sin t)| π/2 0 = - 6
∫ C2 2x ds = - 6
C3:
dx/dt = 0 dy/dt = 1
ds = dt
∫ C3 2x ds = ∫ 0 -3 2 (3) dt = 6 (t)| 0 -3 = 6(- 3) = - 18
∫ C3 2x ds = - 18
بنابراین:
∫ C 2x ds = ∫ C1 2x ds + ∫ C2 2x ds + ∫ C3 2x ds .
= 16 - 6 - 18 = - 8
∫ C 2x ds = - 8 مثال 4 در مثال 1،
یافتهایم : ∫ C 3x 2 ds که در آن C پاره خط از (-1، 1) تا (1،2) است.
در اینجا جهت منحنی را تغییر می دهیم تا ببینیم آیا انتگرال خط تغییر می کند یا خیر:
سپس ∫ -C را 3x 2 ds ارزیابی می کنیم که در آن -C پاره خط از (1,2) (- 1,1 ) است.
فرمول پارامترسازی پاره خطی که از (1، 2) شروع می شود و به (1، 1-) ختم می شود: (t) = (1 - t) 〈1, 2〉 + t 〈- 1,1〉. یعنی: x = (1 - t) (1) + t(- 1) = 1 - 2t y = (1 - t) (2) + t(1) = 2 - t در (1,2): x = 1، y = 2 → t = 0 ، و در (-1، 1): x = - 1، y = 1 →
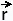
t = 1
بنابراین 0 ≤ t ≤ 1
داریم: dx/dt = - 2، و dy/dt = - 1. از این رو:
ds = √[2 2 + 1 2 ] dt = √5 dt.
ds = √5 dt
بنابراین
∫ -C 3x 2 ds = ∫ 0 1 3(1 - 2t) 2 √5 dt = √5
∫ -C 3x 2 = √5 ، مانند مثال 1.
بنابراین، برای این نوع انتگرال های خط، که برای انتگرال ها با توجه به طول قوس ds است، وقتی جهت منحنی را تغییر می دهیم، انتگرال خط (با توجه به طول قوس) تغییر نمی کند. اما برای همه انتگرال های خط برقرار نیست. برای یک انتگرال خط با توجه به طول قوس، داریم:
∫ C f(x,y) ds = ∫ -C f(x,y) ds
3. انتگرال های خط روی یک منحنی سه بعدی انتگرال های خط روی یک منحنی سه بعدی را می توان از انتگرال های خط روی منحنی دو بعدی گسترش داد.
فرض کنید منحنی سه بعدی C با پارامترسازی داده می شود:
x = x(t)، y = y(t)، z = z(t) a ≤ t ≤ b .
سپس انتگرال خط به صورت زیر داده می شود:
 |
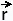
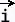
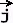
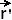
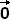
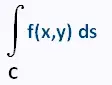
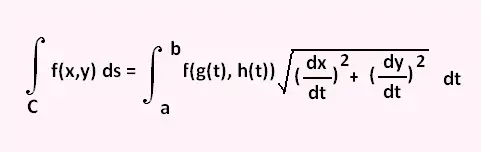





 در این وبلاگ به ریاضیات و کاربردهای آن و تحقیقات در آنها پرداخته می شود. مطالب در این وبلاگ ترجمه سطحی و اولیه است و کامل نیست.در صورتی سوال یا نظری در زمینه ریاضیات دارید مطرح نمایید .در صورت امکان به آن می پردازم. من دوست دارم برای یافتن پاسخ به سوالات و حل پروژه های علمی با دیگران همکاری نمایم.در صورتی که شما هم بامن هم عقیده هستید با من تماس بگیرید.
در این وبلاگ به ریاضیات و کاربردهای آن و تحقیقات در آنها پرداخته می شود. مطالب در این وبلاگ ترجمه سطحی و اولیه است و کامل نیست.در صورتی سوال یا نظری در زمینه ریاضیات دارید مطرح نمایید .در صورت امکان به آن می پردازم. من دوست دارم برای یافتن پاسخ به سوالات و حل پروژه های علمی با دیگران همکاری نمایم.در صورتی که شما هم بامن هم عقیده هستید با من تماس بگیرید.