ادامه مشتق (تعریف)
تعریف
تابع یک متغیر واقعی Y = F ( X ) است مشتقپذیر در یک نقطه از آن دامنه ، اگر حوزه خود شامل یک فاصله باز من حاوی ، و حد
وجود دارد. این بدان معناست که برای هر عدد واقعی مثبت 




که در آن میله های عمودی قدر مطلق را نشان می دهند (به (ε, δ) - تعریف حد مراجعه کنید ).
اگر تابع f را مشتقپذیر در است ، این است که اگر حد L وجود دارد، پس از آن از این حد است به نام مشتق از F در ، و نشان داده می شود

توضیحات
| این مقاله مانند یک کتاب درسی خوانده می شود و ممکن است نیاز به پاکسازی داشته باشد. لطفاً به بهبود این مقاله کمک کنید تا از نظر لحن خنثی و مطابق با استانداردهای کیفیت ویکیپدیا باشد . ( ژوئن 2021 ) |
تمایز عمل محاسبه مشتق است. مشتق تابع y = f ( x ) متغیر x اندازه گیری نرخی است که در آن مقدار y تابع نسبت به تغییر متغیر x تغییر می کند . این است که به نام مشتق از F با توجه به X . اگر X و Y هستند اعداد حقیقی ، و اگر نمودار از F است که در برابر رسم X ، مشتق است شیب این نمودار در هر نقطه
شیب تابع خطی:
ساده ترین حالت، جدا از حالت بی اهمیت یک تابع ثابت ، زمانی است که y یک تابع خطی از x باشد ، به این معنی که نمودار y یک خط است. در این حالت، y = f ( x ) = mx + b ، برای اعداد حقیقی m و b ، و شیب m با
که در آن نماد Δ ( دلتا ) مخفف "تغییر در" و ترکیبات است

{\displaystyle \Delta y=f(x+\Delta x)-f(x)}
فرمول فوق صدق می کند زیرا
بدین ترتیب
این مقدار شیب یک خط را می دهد.
اگر تابع f خطی نباشد (یعنی نمودار آن یک خط مستقیم نباشد)، تغییر در y تقسیم بر تغییر x در محدوده در نظر گرفته شده متفاوت است: تمایز روشی برای یافتن یک مقدار منحصر به فرد برای این نرخ تغییر است. نه در محدوده خاصی
نرخ تغییر به عنوان مقدار حدی
شکل 1 . مماس خط در ( X ، F ( X ))
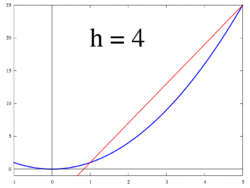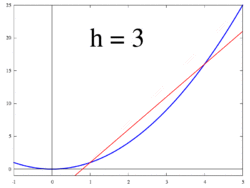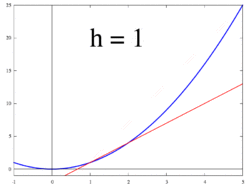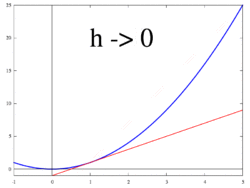
شکل 2. قاطع به منحنی Y = F ( X ) تعیین شده توسط نقطه ( X ، F ( X )) و ( X + ساعت ، F ( X + ساعت ))
شکل 3. خط مماس به عنوان حد برش ها
شکل 4. تصویر متحرک: خط مماس (مشتق) به عنوان حد سکانس ها
ایده ای که توسط شکل های 1 تا 3 نشان داده شده است، محاسبه نرخ تغییر به عنوان مقدار حدی نسبت تفاوت Δ y / Δ x است زیرا Δ x به سمت 0 میل می کند.
به سوی یک تعریف
زمانی که یک سکانت به یک مماس نزدیک می شود 
رایج ترین روش به نوبه خود این ایده بصری به یک تعریف دقیق این است که تعریف مشتق به عنوان یک محدودیت از خارج قسمت تفاوت از اعداد حقیقی. [1] این رویکردی است که در زیر توضیح داده شده است.
فرض کنید f یک تابع با ارزش واقعی باشد که در یک همسایگی باز از یک عدد واقعی a تعریف شده است . در هندسه کلاسیک، خط مماس بر نمودار تابع f در a خط یکتا از نقطه ( a , f ( a )) بود که به صورت عرضی با نمودار f مطابقت نداشت ، به این معنی که خط مستقیم از آن عبور نمی کرد. نمودار مشتق y نسبت به x در a ، از نظر هندسی، شیب خط مماس به نمودار f در است. ( a , f ( a )) . شیب خط مماس بسیار نزدیک به شیب خط از طریق ( a , f ( a )) و یک نقطه نزدیک در نمودار است، به عنوان مثال ( a + h , f ( a + h )) . این خطوط را خطوط برش می گویند . مقدار h نزدیک به صفر تقریب خوبی به شیب خط مماس می دهد و مقادیر کوچکتر (در مقدار مطلق ) h به طور کلی تقریب بهتری را ارائه می دهد.. شیب m خط برش تفاوت بین مقادیر y این نقاط تقسیم بر تفاوت بین مقادیر x است ، یعنی:












 در این وبلاگ به ریاضیات و کاربردهای آن و تحقیقات در آنها پرداخته می شود. مطالب در این وبلاگ ترجمه سطحی و اولیه است و کامل نیست.در صورتی سوال یا نظری در زمینه ریاضیات دارید مطرح نمایید .در صورت امکان به آن می پردازم. من دوست دارم برای یافتن پاسخ به سوالات و حل پروژه های علمی با دیگران همکاری نمایم.در صورتی که شما هم بامن هم عقیده هستید با من تماس بگیرید.
در این وبلاگ به ریاضیات و کاربردهای آن و تحقیقات در آنها پرداخته می شود. مطالب در این وبلاگ ترجمه سطحی و اولیه است و کامل نیست.در صورتی سوال یا نظری در زمینه ریاضیات دارید مطرح نمایید .در صورت امکان به آن می پردازم. من دوست دارم برای یافتن پاسخ به سوالات و حل پروژه های علمی با دیگران همکاری نمایم.در صورتی که شما هم بامن هم عقیده هستید با من تماس بگیرید.