ادامه گروه دو وجهی(3)
نمایش ماتریس [ ویرایش ]
تقارن های این پنج ضلعی تبدیل خطی صفحه به عنوان یک فضای بردار است.
اگر ما مرکز چند ضلعی منظم در مبدا، عناصر پس از آن از عمل گروه دو وجهی به عنوان تبدیلات خطی از فضا . این به ما امکان می دهد عناصر D n را به عنوان ماتریس نشان دهیم ، با ترکیب ضرب ماتریس . این نمونه ای از یک (2 بعدی) است نمایندگی گروه .
به عنوان مثال ، عناصر گروه D 4 را می توان با هشت ماتریس زیر نشان داد:
به طور کلی ، ماتریس های عناصر D n شکل زیر را دارند:
r k یک ماتریس دورانی است که یک حرکت خلاف جهت عقربه های ساعت را از زاویه 2 πk / n بیان می کند . s k بازتابی در طول خط است که با محور x زاویه πk / n ایجاد می کند .
تعاریف دیگر [ ویرایش ]
تعاریف معادل دیگری از D n عبارتند از:
- گروه خودریختی از نمودار فقط متشکل از یک دوران با N راس (اگر N ≥ 3).
- گروه با ارائه
از ارائه دوم نتیجه می گیرد که D n به گروه گروه های کاکستر تعلق دارد . - ضرب نیم مستقیم از گروه های دوران های Z N و Z 2 ، با Z 2 اقدام در Z N توسط وارونگی (به این ترتیب، D N همیشه یک زیرگروه نرمال ریخت به گروه Z N ). Z N ⋊ φ Z 2 به ریخت است D N اگر φ (0) است همانی و φ (1) وارونگی است.
گروههای کوچک دوضلعی [ ویرایش ]
نمونه های فرعی از تقارن دو ضلعی شش ضلعی
D 1 است ریخت به Z 2 از گروه دوری از مرتبه 2.
D 2 است ریخت به K 4 از گروه چهارتایی کلاین .
D 1 و D 2 از این جهت استثنا هستند:
- D 1 و D 2 تنها هستند آبلی گروه دو وجهی. در غیر این صورت ، D n غیر ابلیان نیست.
- D N است زیر گروه از گروه متقارن S N برای N ≥ 3 . از 2 n > n ! برای n = 1 یا n = 2 ، برای این مقادیر ، D n بسیار بزرگتر از آن است که یک زیر گروه باشد.
- گروه خودریختی داخلی D 2 بی اهمیت است، در حالی که برای دیگر ارزش حتی از N ، این است D N / Z 2 .
گراف دوری از گروه دو وجهی از تشکیل N دوران -Element و N دوران 2-عنصر. راس تیره در نمودارهای دوران زیر گروههای مختلف دوضلعی نشان دهنده عنصر همانی است و سایر راسها دیگر عناصر گروه هستند. یک دوران شامل نیروهای پی در پی هر یک از عناصر متصل به عنصر همانی است .
| D 1 = Z 2 | D 2 = Z 2 2 = K 4 | D 3 | D 4 | D 5 |
|---|---|---|---|---|
 |  |  |  |  |
 |  |  | 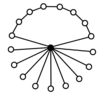 |  |
| D 6 = D 3 × Z 2 | D 7 | D 8 | D 9 | D 10 = D 5 × Z 2 |
| D 3 = S 3 | D 4 |
|---|---|
 |  |

![{\ displaystyle {\ begin {matrix} \ mathrm {r} _ {0} = \ left ({\ begin {smallmatrix} 1 & 0 \\ [0.2em] 0 & 1 \ end {smallmatrix}} \ right) ، و \ mathrm { r} _ {1} = \ left ({\ begin {smallmatrix} 0 & -1 \\ [0.2em] 1 & 0 \ end {smallmatrix}} \ راست) ، و \ mathrm {r} _ {2} = \ left ( {\ begin {smallmatrix} -1 & 0 \\ [0.2em] 0 & -1 \ end {smallmatrix}} \ راست) ، و \ mathrm {r} _ {3} = \ left ({\ begin {smallmatrix} 0 & 1 \\ [0.2em] -1 & 0 \ end {smallmatrix}} \ right) ، \\ [1em] \ mathrm {s} _ {0} = \ left ({\ begin {smallmatrix} 1 & 0 \\ [0.2em] 0 & -1 \ end {smallmatrix}} \ right) ، و \ mathrm {s} _ {1} = \ left ({\ begin {smallmatrix} 0 & 1 \\ [0.2em] 1 & 0 \ end {smallmatrix}} \ right) ، و \ \ mathrm {s} _ {2} = \ left ({\ begin {smallmatrix} -1 & 0 \\ [0.2em] 0 & 1 \ end {smallmatrix}} \ right) ، و \ mathrm {s} _ {3} = \ left ({\ begin {smallmatrix} 0 & -1 \\ [0.2em] -1 & 0 \ end {smallmatrix}} \ راست). \ end {matrix}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/c72296b4c5f5de93a62ee7d535c60589b3da46cb)



 در این وبلاگ به ریاضیات و کاربردهای آن و تحقیقات در آنها پرداخته می شود. مطالب در این وبلاگ ترجمه سطحی و اولیه است و کامل نیست.در صورتی سوال یا نظری در زمینه ریاضیات دارید مطرح نمایید .در صورت امکان به آن می پردازم. من دوست دارم برای یافتن پاسخ به سوالات و حل پروژه های علمی با دیگران همکاری نمایم.در صورتی که شما هم بامن هم عقیده هستید با من تماس بگیرید.
در این وبلاگ به ریاضیات و کاربردهای آن و تحقیقات در آنها پرداخته می شود. مطالب در این وبلاگ ترجمه سطحی و اولیه است و کامل نیست.در صورتی سوال یا نظری در زمینه ریاضیات دارید مطرح نمایید .در صورت امکان به آن می پردازم. من دوست دارم برای یافتن پاسخ به سوالات و حل پروژه های علمی با دیگران همکاری نمایم.در صورتی که شما هم بامن هم عقیده هستید با من تماس بگیرید.