ریاضیات

همانطور که از نامش مشخص است ، گروه کواترنیون زیر گروه ضربی کواترنیونهای همیلتونی است که هشت عنصر را تولید کرده و روابط ایجاد می کند . میز Cayley آن است

قدرت عناصر گروه کواترنیون عبارتند از:

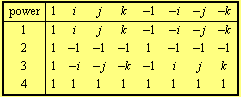
معمولاً با آن نشان داده می شود . این یکی از دو گروه غیرآبلی از پنج گروه محدود کلی از مرتبه 8 است. (گروه دوم گروه دی هدرال است ).

قضیه لاگرانژ نشان می دهد که هر زیرگروه سرهباید باشد یا مرتبه 2 یا 4. است یک زیر گروه منحصر به فرد از سفارش 2 وجود دارد، یعنی ، و سه زیر گروه از سفارش 4: ، ، و .

مرکز آن است . گروه فاکتور نسبت به چهار گروه کلاین ایزومورف است . علاوه بر این ، گروه کواترنیون تنها گروهی است که همه زیر گروه های مناسب هابلی و نرمال هستند

گروه کواترنیون کوچکترین گروه دو حلقه ای است.

این کوچکترین نمونه از گروههای به اصطلاح همیلتونی است ، که گروههایی هستند که هر زیر گروهی از آنها یک گروه نرمال است. هر گروه همیلتونی حاوی یک نسخه از .

همچنین می تواند توسط روابط تولید کننده یا ، به عنوان گروهی که توسط دو عنصر ایجاد شده است ، و هر دو از مرتبه 4 تابع روابط و . این به جدول Cayley می دهد

ایزومورفیسم بین این دو شکل توسط قوانین ارائه می شود: ، ، ، .

همچنین می توان گروه را از نظر جایگزینی به عنوان زیر گروهی از گروه ارائه کرد  . با جایگزینی و . سپس
،
،
،
و
.

منبع

https://www.cs.cas.cz/portal/AlgoMath/AlgebraicStructures/StructuresWithOneOperation/Groups/SpecialGroups/QuaternionGroup.htm