پنهان شدناین مقاله دارای چندین مسئله است. لطفاً در بهبود آن كمك كنید یا این موارد را در صفحه بحث مطرح كنید. (با نحوه و زمان حذف این پیام های الگو آشنا شوید )

این مقاله نیاز به توجه یک متخصص ریاضیات دارد . ( مارس 2011 )

این مقاله لیستی از منابع عمومی را شامل می شود ، اما تا حد زیادی تأیید نشده باقی می ماند زیرا فاقد استنادات درون ریز مربوطه است . ( اکتبر 2019 )

در فیزیک ریاضی ، سیستم هیلبرت اصطلاحی است که به ندرت برای یک سیستم فیزیکی که توسط جبر C * توصیف می شود ، استفاده می شود .

در منطق ، به ویژه منطق ریاضی ، یک سیستم هیلبرت ، که گاهی اوقات حساب دیفرانسیل هیلبرت ، سیستم قیاسی به سبک هیلبرت یا سیستم هیلبرت-آکرمان نامیده می شود ، نوعی سیستم کسر رسمی است که به گوتلوب فرگه [1] و دیوید هیلبرت نسبت داده می شود . این سیستمهای قیاسی اغلب برای منطق مرتبه اول مورد مطالعه قرار می گیرند ، اما برای منطقهای دیگر نیز مورد توجه هستند.

ترین انواع سیستم های هیلبرت یک رویه مشخصه در راه آنها تعادل تجارت کردن بین بدیهیات منطقی و قواعد استنتاج . [1] سیستم های هیلبرت را می توان با انتخاب تعداد زیادی از طرح های بدیهی منطقی و مجموعه کوچکی از قوانین استنباط مشخص کرد . سیستم های کسر طبیعی ، عکس معکوس دارند ، از جمله بسیاری از قوانین کسر ، اما طرح های بدیهی بسیار کم یا بدون آن. سیستم های هیلبرت که معمولاً مورد مطالعه قرار می گیرند یا فقط یک قاعده استنباط دارند - modus ponens ، برای منطق گزاره ای  - یا دو - با تعمیم ،منطق محمول ، و همچنین - چندین طرح بدیهی بی نهایت. سیستمهای هیلبرت برای منطقهای گزاره ای پیشنهادی ، كه بعضاً سیستمهای Hilbert-Lewis نامیده می شوند ، به طور كلی با دو قانون اضافی ، قانون ضروری و قانون جایگزینی یكنواخت ، بدیهی می شوند.

یک ویژگی مشخصه از بسیاری از انواع سیستم های هیلبرت این است که زمینه در هیچ یک از قوانین استنباط آنها تغییر نمی کند ، در حالی که هم کسر طبیعی و هم حساب انتهایی شامل برخی از قوانین تغییر دهنده زمینه است. بنابراین ، اگر کسی فقط به قابلیت تحقق توتولوژی ، و هیچ قضاوت فرضی علاقه مند باشد ، می توان سیستم هیلبرت را رسمیت داد به گونه ای که قواعد استنباط آن فقط حاوی قضاوت هایی از یک شکل نسبتاً ساده باشد. همین کار را نمی توان با دو سیستم کسر دیگر انجام داد: [ نیاز به منبع ] با تغییر زمینه در برخی از قوانین استنباط آنها ، نمی توان آنها را رسمیت داد تا از قضاوتهای فرضی جلوگیری شود - حتی اگر ما بخواهیم از آنها فقط برای اثبات قابلیت تحقق توتولوژی استفاده کنیم.

 

فهرست

کسر رسمی [ ویرایش ]

نمایش گرافیکی سیستم کسر

در سیستم کسر به سبک هیلبرت ، کسر رسمی توالی متناهی از فرمول ها است که در آن هر فرمول یا یک بدیهی است یا از طریق فرمول استنباط از فرمول های قبلی بدست می آید. این کسورات رسمی به منظور تأیید دلایل اثبات زبان طبیعی است ، اگرچه جزئیات آن بسیار بیشتر است.

فرض کنید \ گاما مجموعه ای از فرمول ها است که به عنوان فرضیه در نظر گرفته می شود . مثلا،\ گاما می تواند مجموعه ای از بدیهیات برای نظریه گروه یا نظریه مجموعه باشد . علامت گذاری\ گاما \ vdash \ فی به این معنی است که کسری وجود دارد که به پایان می رسد \ فی با استفاده از بدیهیات فقط بدیهیات منطقی و عناصر\ گاما . بنابراین ، به طور غیررسمی ،\ گاما \ vdash \ فی یعنی که\ فی  با فرض تمام فرمول های موجود قابل اثبات است \ گاما .

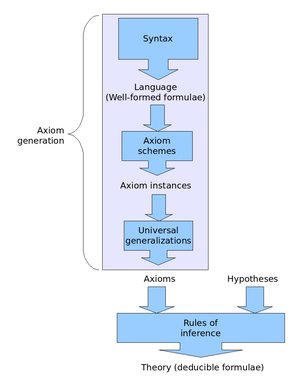
سیستم های استنباط به سبک هیلبرت با استفاده از طرح های متعدد بدیهیات منطقی مشخص می شوند . طرح اصل یک مجموعه نامتناهی از بدیهیات به دست آمده با جایگزین تمام فرمول از نوعی به یک الگوی خاص است. مجموعه بدیهیات منطقی نه تنها شامل بدیهیات تولید شده از این الگو ، بلکه همچنین شامل هرگونه تعمیم یکی از این بدیهیات است. تعمیم فرمول با پیش شماره گذاری صفر یا بیشتر جهانی در فرمول بدست می آید. مثلا\ forall y (\ forall x Pxy \ به Pty) تعمیم است \ forall x Pxy \ به Pty.

بدیهیات منطقی [ ویرایش ]

چندین بدیهی سازی متنوع از منطق محمول وجود دارد ، زیرا برای هر منطقی در انتخاب بدیهیات و قواعدی که این منطق را مشخص می کنند ، آزادی وجود دارد. ما در اینجا یک سیستم هیلبرت با نه بدیهی و فقط حالت معادل قانون را توصیف می کنیم ، که ما آن را اصطلاح سازی یک قاعده می نامیم و منطق معادله ای کلاسیک را توصیف می کند. ما برای این منطق با حداقل زبان سروکار داریم ، جایی که فرمول ها فقط از رابط ها استفاده می کنند\ نه  و \به  و فقط مقدار دهنده \برای همه . بعداً نشان می دهیم که چگونه می توان سیستم را گسترش داد تا شامل اتصالات منطقی اضافی مانند موارد دیگر شود\زمین  و \ lor ، بدون بزرگ کردن کلاس فرمول های قابل کسر.

چهار طرح بدیهی منطقی برای دستکاری اتصالات منطقی (همراه با مد پوننس) امکان پذیر است.

P1 \ phi \ به \ phi

P2 \ phi \ به \ چپ (\ psi \ به \ phi \ راست)

\ چپ (\ phi \ به \ چپ (\ psi \ rightarrow \ xi \ راست) \ راست) \ به \ چپ (\ چپ (\ phi \ به \ psi \ راست) \ به \ چپ (\ phi \ به \ xi \ راست) \ راست)

P4 \ چپ (\ lnot \ phi \ به \ lnot \ psi \ راست) \ به \ چپ (\ psi \ به \ phi \ راست)

همانطور که از P3 ، P2 و modus ponens بر می آید بدیهی P1 زائد است (به بخش اثبات مراجعه کنید ). این بدیهیات منطق گزاره ای کلاسیک را توصیف می کنند . بدون اصل P4 منطق استدلال مثبت دریافت می کنیم . منطق حداقلی یا با افزودن بدیهی P4m یا با تعریف بدست می آید\ ln \ phi نیست مانند \ phi \ به \ bot.

\ چپ (\ phi \ به \ psi \ راست) \ به \ چپ (\ چپ (\ phi \ به \ lnot \ psi \ راست) \ به \ lnot \ phi \ راست)

منطق شهود گرایی با افزودن بدیهیات P4i و P5i به منطق استدلال مثبت یا با افزودن بدیهی P5i به منطق حداقلی حاصل می شود. P4i و P5i هر دو قضیه منطق گزاره ای کلاسیک هستند.

P4i \ چپ (\ phi \ به \ lnot \ phi \ راست) \ به \ lnot \ phi

P5i \ lnot \ phi \ به \ چپ (\ phi \ به \ psi \ راست)

توجه داشته باشید که اینها طرح های بدیهی است ، که نمایانگر موارد بسیار خاصی از بدیهیات است. به عنوان مثال ، P1 ممکن است نمونه بدیهی خاصی را نشان دهدp \ به p ، یا ممکن است نشان دهد \ چپ (p \ به q \ راست) \ به \ چپ (p \ به q \ راست) : \ فی مکانی است که می توان هر فرمولی را در آن قرار داد. یک متغیر مانند این که بیش از فرمول ها باشد ، "متغیر شماتیک" نامیده می شود.

با یک قانون دوم جایگزینی یکنواخت (US) ، می توانیم هر یک از این طرح های بدیهی را به یک بدیهی واحد تبدیل کنیم و هر متغیر شماتیک را با برخی متغیرهای گزاره ای که در هیچ بدیه ای ذکر نشده است جایگزین کنیم تا آنچه را که بدیهی سازی جایگزین می نامیم بدست آوریم. هر دو رسمیت متغیرهایی دارند ، اما در مواردی که بدیهی سازی یک قاعده دارای متغیرهای شماتیک است که خارج از زبان منطق هستند ، بدیهی سازی جایگزینی از متغیرهای پیشنهادی استفاده می کند که با بیان ایده متغیری از فرمول ها با یک قانون استفاده از جایگزینی ، کار مشابهی را انجام می دهند.

آمریکا اجازه دهید\ phi (p) فرمولی با یک یا چند نمونه از متغیر گزاره ای باشدپ، و اجازه دهید \ psi فرمول دیگری باشد. سپس از\ phi (p)، نتیجه گیری \ phi (\ psi). [ مشکوک - بحث کنید]

سه طرح بدیهی منطقی بعدی ، روشهایی را برای افزودن ، دستکاری و حذف کمیت سنجهای جهانی ارائه می دهند.

Q5  \ forall x \ چپ (\ phi \ راست) \ به \ phi [x: = t]که در آن T ممکن است برای جایگزین X در\ ، \! \ فی

Q6 \ forall x \ چپ (\ phi \ به \ psi \ راست) \ به \ چپ (\ forall x \ چپ (\ phi \ راست) \ به \ forall x \ چپ (\ psi \ راست) \ راست)

Q7 \ phi \ به \ forall x \ چپ (\ phi \ راست) جایی که x در آن آزاد نیست\ فی .

این سه قاعده اضافی سیستم گزاره ای را گسترش می دهد تا منطق محمول کلاسیک را بدیهی کند . به همین ترتیب ، این سه قاعده سیستم را برای منطق گزاره ای شهودی (با P1-3 و P4i و P5i) به منطق محمول شهودی گسترش می دهند .

کمی سازی جهانی معمولاً با استفاده از یک قانون اضافی تعمیم ، یک بدیهی سازی جایگزین داده می شود (به بخش متا تئورم مراجعه کنید) ، در این حالت قوانین Q6 و Q7 زائد هستند. [ مشکوک - بحث کنید]

طرح های بدیهی نهایی برای کار با فرمول های مربوط به نماد برابری مورد نیاز است.

I8 x = xبرای هر متغیر x .

I9 \ چپ (x = y \ راست) \ به \ چپ (\ phi [z: = x] \ به \ phi [z: = y] \ راست)

افزونه های محافظه کارانه [ ویرایش ]

معمولاً در سیستم استنباط به سبک هیلبرت فقط بدیهیاتی برای استنباط و نفی گنجانده می شود. با توجه به این اصول موضوعه، ممکن است به شکل پسوند محافظه کار از قضیه کسر که اجازه استفاده از ادات اضافی. این پسوندها محافظه کارانه خوانده می شوند زیرا اگر فرمولی φ شامل اتصالات جدید به عنوان یک فرمول منطقی معادل θ که فقط شامل نفی ، استنتاج و کمی سازی جهانی است ، بازنویسی شود ، در این صورت φ فقط در صورت استخراج θ در سیستم اصلی در سیستم توسعه یافته قابل استخراج است . وقتی کاملاً گسترش یابد ، یک سیستم به سبک هیلبرت بیشتر شبیه یک سیستم کسر طبیعی خواهد بود .

کمی سازی وجودی [ ویرایش ]

  • معرفی

\ forall x (\ phi \ به \ وجود y (\ phi [x: = y])))

  • حذف

\ forall x (\ phi \ به \ psi) \ به \ وجود x (\ phi) \ به \ psi  جایی که ایکسیک متغیر آزاد از نیست\ psi .

پیوند و انشعاب [ ویرایش ]

  • معرفی و حذف اتصال

معرفی:  \ alpha \ به \ beta \ به \ alpha \ land \ beta

حذف باقی مانده:  \ alpha \ wedge \ beta \ به \ alpha

حق حذف:  \ alpha \ wedge \ beta \ به \ beta

  • معرفی و حذف گسیختگی

معرفی مانده:  \ alpha \ به \ alpha \ vee \ beta

معرفی درست:  \ beta \ به \ alpha \ vee \ beta

حذف:  (\ آلفا \ به \ گاما) \ به (\ بتا \ به \ گاما) \ به \ آلفا \ vee \ بتا \ به \ گاما

فرادارگان [ ویرایش ]

از آنجا که سیستم های سبک هیلبرت قوانین کسر بسیار کمی دارند ، اثبات متادئورمی که نشان می دهد قوانین کسر اضافی هیچ قدرت استنباطی ندارند ، معمول است ، به این معنا که کسر با استفاده از قوانین جدید کسر فقط با کسر اصلی قابل کسر است. قوانین

برخی از فرادارهای متداول این فرم عبارتند از:

  • قضیه کسر :\ گاما ؛ \ phi \ vdash \ psi اگر و تنها اگر \ گاما \ vdash \ phi \ به \ psi.
  • \ Gamma \ vdash \ phi \ leftrightarrow \ psi اگر و تنها اگر \ گاما \ vdash \ phi \ به \ psi و \ گاما \ vdash \ psi \ به \ phi.
  • تناقض: اگر \ گاما ؛ \ phi \ vdash \ psi سپس \ Gamma؛ \ lnot \ psi \ vdash \ lnot \ phi.
  • تعمیم : اگر\ گاما \ vdash \ فیو x در هیچ فرمولی از آزاد وجود ندارد\ گاما  سپس \ Gamma \ vdash \ forall x \ phi.

 

برخی از قضیه های مفید و اثبات آنها [ ویرایش ]

در زیر چندین قضیه در منطق گزاره ای ، همراه با اثبات آنها (یا پیوند به این اثبات ها در سایر مقالات) آورده شده است. توجه داشته باشید که از آنجا که (P1) با استفاده از سایر بدیهیات قابل اثبات است ، در حقیقت (P2) ، (P3) و (P4) برای اثبات همه این قضیه ها کافی است.

(HS1) {\ displaystyle (q \ to r) \ به ((p \ به q) \ به (p \ به r))}}- قیاس فرضی ، اثبات را ببینید .

(L1) {\ displaystyle p \ به ((p \ به q) \ به q)} - اثبات:

(1) {\ displaystyle ((p \ به q) \ به (p \ به q)) \ به (((p \ به q) \ به p) \ به ((p \ به q) \ به q))}}       (نمونه (P3))

(2){\ displaystyle (p \ to q) \ به (p \ to q)}       (نمونه (P1))

(3) {\ displaystyle ((p \ به q) \ به p) \ به ((p \ به q) \ به q)}       (از (2) و (1) توسط modus ponens )

(4) {\ displaystyle (((p \ to q) \ به p) \ به ((p \ به q) \ به q)) \ به ((p \ به ((p \ به q) \ به p)) \ به (p \ به ((p \ به q) \ به q)))}}       (نمونه (HS1))

(5) {\ displaystyle (p \ به ((p \ به q) \ به p)) \ به (p \ به ((p \ به q) \ به q))}}       (از (3) و (4) توسط modus ponens)

(6) {\ displaystyle p \ به ((p \ به q) \ به p)}       (نمونه (P2))

(7) {\ displaystyle p \ به ((p \ به q) \ به q)}       (از (6) و (5) توسط modus ponens)

دو قضیه زیر با هم به عنوان دو نفی شناخته می شوند :

(DN1){\ displaystyle \ neg \ neg p \ به p}

(DN2) {\ displaystyle p \ to \ neg \ neg p}

اثبات را ببینید .

(L2) {\ displaystyle (p \ به (q \ to r)) \ به (q \ به (p \ to r))}}- برای این اثبات ، ما از روش متا تئورم فرضیه داستانی به عنوان خلاصه ای برای چندین مرحله اثبات استفاده می کنیم:

(1){\ displaystyle (p \ به (q \ to r)) \ به ((p \ به q) \ به (p \ به r))}}       (نمونه (P3))

(2){\ displaystyle ((p \ به q) \ به (p \ to r)) \ به ((q \ به (p \ به q))} \ به (q \ به (p \ به r)))}}       (نمونه (HS1))

(3) {\ displaystyle (p \ به (q \ to r)) \ به ((q \ به (p \ به q))} \ به (q \ به (p \ به r)))}}       (از (1) و (2) با استفاده از متاورامای فرضیه سلولیسم)

(4) {\ displaystyle ((p \ به (q \ to r)) \ به ((q \ به (p \ به q))) \ به (q \ به (p \ به r))))} \ به (((p \ به (q \ به r)) \ به (q \ به (p \ به q)))) \ به ((p \ به (q \ به r)) \ به (q \ به (p \ به r)) ))}       (نمونه (P3))

(5) {\ displaystyle ((p \ به (q \ به r)) \ به (q \ به (p \ به q)))) \ به ((p \ به (q \ به r)) \ به (q \ به ( p \ به r)))}       (از (3) و (4) با استفاده از modus ponens)

(6) {\ displaystyle q \ to (p \ to q)}       (نمونه (P2))

(7) {\ displaystyle (q \ به (p \ to q)) \ به ((p \ به (q \ به r))} \ به (q \ به (p \ به q)))}}       (نمونه (P2))

(8){\ displaystyle (p \ به (q \ to r)) \ به (q \ به (p \ to q))}}       (از (6) و (7) با استفاده از modus ponens)

(9){\ displaystyle (p \ به (q \ to r)) \ به (q \ به (p \ to r))}}       (از (8) و (5) با استفاده از modus ponens)

(HS2) {\ displaystyle (p \ to q) \ به ((q \ to r) \ به (p \ to r))}}- یک شکل جایگزین هم اندیشی فرضی . اثبات:

(1) {\ displaystyle (q \ to r) \ به ((p \ به q) \ به (p \ به r))}}       (نمونه (HS1))

(2) {\ displaystyle ((q \ to r) \ به ((p \ به q) \ به (p \ به r)))} \ به ((p \ به q) \ به ((q \ به r) \ به ( p \ به r)))}       (نمونه (L2))

(3){\ displaystyle (p \ to q) \ به ((q \ to r) \ به (p \ to r))}} (از (1) و (2) توسط modus ponens)

(TR1) {\ displaystyle (p \ to q) \ to (\ neg q \ to \ neg p)}- جابجایی ، اثبات را ببینید (جهت دیگر جابجایی (P4) است).

(TR2) {\ displaystyle (\ neg p \ to q) \ به (\ neg q \ to p)}- شکل دیگری از جابجایی ؛ اثبات:

(1) {\ displaystyle (\ neg p \ to q) \ به (\ neg q \ to \ neg \ neg p)}}       (نمونه (TR1))

(2){\ displaystyle \ neg \ neg p \ به p}       (نمونه (DN1))

(3){\ displaystyle (\ neg \ neg p \ to p) \ به ((\ neg q \ به \ neg \ neg p) \ به (\ neg q \ به p))}}       (نمونه (HS1))

(4) {\ displaystyle (\ neg q \ to \ neg \ neg p) \ به (\ neg q \ to p)}       (از (2) و (3) توسط modus ponens)

(5){\ displaystyle (\ neg p \ to q) \ به (\ neg q \ to p)}       (از (1) و (4) با استفاده از فرضیه فرضیه سلولیسم)

(L3) {\ displaystyle (\ neg p \ to p) \ به p} - اثبات:

(1) {\ displaystyle \ neg p \ to (\ neg \ neg (q \ to q) \ به \ neg p)}       (نمونه (P2))

{\ displaystyle (\ neg \ neg (q \ to q) \ به \ neg p) \ به (p \ to \ neg (q \ to q))}}       (نمونه (P4))

{\ displaystyle \ neg p \ به (p \ به \ neg (q \ به q))}}       (از (1) و (2) با استفاده از متاورامای فرضیه سلولیسم)

{\ displaystyle (\ neg p \ to (p \ to \ neg (q \ to q)))) \ to ((\ neg p \ to p) \ به (\ neg p \ to \ neg (q \ to q) ))}       (نمونه (P3))

{\ displaystyle (\ neg p \ to p) \ به (\ neg p \ to \ neg (q \ to q))}}       (از (3) و (4) با استفاده از حالت های ponens)

{\ displaystyle (\ neg p \ to \ neg (q \ to q)) \ به ((q \ to q) \ به p)}       (نمونه (P4))

{\ displaystyle (\ neg p \ to p) \ به ((q \ به q) \ به p)}       (از (5) و (6) با استفاده از فرضیه فرضیه سلولیسم)

(8) {\ displaystyle q \ to q}       (نمونه (P1))

(9) {\ displaystyle (q \ به q) \ به (((q \ به q) \ به p) \ به p)}       (نمونه (L1))

(10) {\ displaystyle ((q \ به q) \ به p) \ به p}       (از (8) و (9) با استفاده از حالت های ponens)

(11) {\ displaystyle (\ neg p \ to p) \ به p}       (از (7) و (10) با استفاده از فرضیه فرضیه سلولیسم)

بدیهی سازی های جایگزین [ ویرایش ]

اطلاعات بیشتر: لیست سیستم های منطقی

بدیهیات 3 فوق به toukasiewicz اعتبار دارد . [2] سیستم اصلی توسط Frege دارای بدیهیات P2 و P3 بود اما به جای اصل P4 چهار اصل دیگر (نگاه کنید به حساب گزاره ای فرگه ). راسل و وایتهد همچنین سیستمی با پنج بدیهی گزاره را پیشنهاد داده اند.

ارتباطات بعدی [ ویرایش ]

بدیهیات P1 ، P2 و P3 ، با قاعده کسر modus ponens (رسمی سازی منطق گزاره ای شهودی ) ، با ترکیب کننده های پایه منطق ترکیبی I ، K و S با عملگر برنامه مطابقت دارند . اثبات های موجود در سیستم هیلبرت در منطق ترکیبی با اصطلاحات ترکیبی مطابقت دارند. همچنین به مکاتبات کاری-هوارد مراجعه کنید .

همچنین به [ ویرایش ] مراجعه کنید

یادداشت ها [ ویرایش ]

  1. ^ پرش به بالا به:a b Máté & Ruzsa 1997: 129
  2. ^ A. Tarski ، منطق ، معناشناسی ، فراتمادی ، آکسفورد ، 1956

منابع [ ویرایش ]

https://en.wikipedia.org/wiki/Hilbert_system


  •