ریاضیات

استرس ساده [ ویرایش ]

در بعضی شرایط ، تنش درون بدن ممکن است به اندازه کافی توسط یک عدد منفرد ، یا توسط یک بردار منفرد (یک عدد و یک جهت) توصیف شود. سه موقعیت تنش ساده از این قبیل که اغلب در طراحی مهندسی مشاهده می شود ، تنش طبیعی تک محوره ، تنش برشی ساده و فشار طبیعی ایزوتروپیک است . [9]

استرس طبیعی تک محوره [ ویرایش ]

استرس ایده آل در یک میله مستقیم با مقطع یکنواخت.

یک وضعیت معمول با یک الگوی تنش ساده این است که یک میله مستقیم ، با مواد یکنواخت و مقطع عرضی ، تحت فشار نیروهای مخالف تحت فشار قرار می گیرد{\ displaystyle F}در امتداد محور خود. اگر سیستم در تعادل است و با گذشت زمان تغییر نمی کند و می توان از وزن میله غافل شد ، پس از طریق هر قسمت عرضی میله ، قسمت بالایی باید با همان نیرو بر روی قسمت پایین بکشد ، F با تداوم از طریق کامل سطح مقطع ، A . بنابراین ، تنش σ در سراسر میله ، در سرتاسر سطح افقی ، به سادگی با عدد واحد σ قابل بیان است که به سادگی با اندازه آن نیروها ، F و سطح مقطع ، A محاسبه می شود .

از طرف دیگر ، اگر کسی تصور کند که میله در امتداد طول آن ، به موازات محور ، بریده شده است ، هیچ نیرویی (از این رو هیچ استرسی) بین دو نیمه در طول برش وجود نخواهد داشت.

این نوع استرس را می توان استرس طبیعی (استرس) یا استرس تک محوری نامید. به طور خاص ، (کشش تک محوری ، ساده و غیره) تنش کششی. [9] اگر بار به جای کشش ، فشار روی میله باشد ، تجزیه و تحلیل یکسان است با این تفاوت که نیروی F و تنش علامت تغییر ، و تنش را فشار فشاری می نامند.

نسبت ممکن است فقط یک استرس متوسط ​​باشد. تنش ممکن است به طور ناهموار در سطح مقطع ( متر - متر ) توزیع شود ، به ویژه در نزدیکی نقاط اتصال ( n - n ).

این تحلیل فرض می کند استرس به طور مساوی در کل سطح مقطع توزیع شده است. در عمل ، بسته به نحوه اتصال میله در انتها و نحوه تولید آن ، ممکن است این فرض معتبر نباشد. در این صورت ، مقدار= F / A فقط تنش متوسط ​​خواهد بود که به آن تنش مهندسی یا تنش اسمی گفته می شود . با این حال اگر طول نوار L بسیاری از برابر قطر خود است D ، و آن را بدون نقص ناخالص و یا ساخته شده در استرس ، سپس استرس می توان فرض به صورت یکنواخت بر روی هر مقطع است که بیش از چند بار توزیع D از هر دو به پایان می رسد. (این مشاهده به عنوان اصل سنت وننت شناخته می شود ).

تنش طبیعی علاوه بر کشش محوری و فشرده سازی در بسیاری از موقعیت های دیگر نیز رخ می دهد. اگر یک میله الاستیک با مقطع یکنواخت و متقارن در یکی از صفحات تقارن آن خم شود ، تنش خمشی حاصل همچنان نرمال خواهد بود (عمود بر سطح مقطع) ، اما در سطح مقطع متفاوت خواهد بود: قسمت بیرونی تحت تنش کششی قرار بگیرید ، در حالی که قسمت داخلی فشرده می شود. نوع دیگر تنش طبیعی ، فشار حلقه ای است که روی دیواره های لوله استوانه ای یا ظرف پر از مایع تحت فشار ایجاد می شود.

تنش برشی ساده [ ویرایش ]

تنش برشی در یک میله افقی که توسط دو بلوک جبران بار شده است.

نوع ساده دیگر تنش هنگامی اتفاق می افتد که یک لایه ضخیم یکنواخت از مواد الاستیک مانند چسب یا لاستیک محکم به دو جسم سفت متصل شود که توسط نیروهای موازی لایه در جهات مخالف کشیده می شوند. یا بخشی از یک میله فلزی نرم که توسط فک ابزار قیچی مانند بریده می شود . بگذارید F مقدار آن نیروها باشد و M میانه هواپیما آن لایه باشد. دقیقاً مانند حالت تنش طبیعی ، بخشی از لایه در یک طرف M باید قسمت دیگر را با همان نیروی F بکشد . با فرض معلوم بودن جهت نیروها ، تنش را در M می توان به سادگی با عدد واحد بیان کرد، به سادگی با اندازه آن نیروها ، F و سطح مقطع ، A محاسبه می شود .

با این حال ، بر خلاف تنش طبیعی ، این تنش برشی ساده به جای عمود بر آن ، به موازات مقطع در نظر گرفته شده است. [9] برای هر صفحه S که عمود بر لایه باشد ، نیروی داخلی خالص در سراسر S و از این رو تنش صفر خواهد بود.

همانطور که در مورد میله محوری بارگذاری می شود ، در عمل ممکن است تنش برشی به طور یکنواخت روی لایه توزیع نشود. بنابراین ، مانند گذشته ، نسبت F / A فقط یک فشار متوسط ​​("اسمی" ، "مهندسی") خواهد بود. با این حال ، این میانگین اغلب برای اهداف عملی کافی است. [10] : p.292 تنش برشی نیز هنگامی مشاهده می شود که یک میله استوانه ای مانند شافت در انتهای آن تحت گشتاورهای مخالف قرار گیرد. در آن حالت ، تنش برشی در هر مقطع موازی مقطع است ، اما به طور مماس نسبت به محور جهت دارد و با فاصله از محور افزایش می یابد. تنش برشی قابل توجهی در صفحه میانی ("وب") پرتوهای I رخ می دهد تحت بارهای خمشی ، به دلیل وب محدود کننده صفحات انتهایی ("فلنج").

استرس ایزوتروپیک [ ویرایش ]

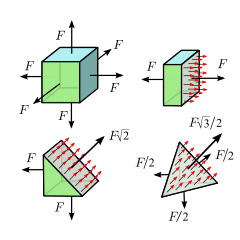
تنش کششی ایزوتروپیک. بالا سمت چپ: هر وجه یک مکعب از مواد همگن توسط نیرویی به بزرگی F کشیده می شود ، که به طور مساوی در کل صورت که مساحت آن A است اعمال می شود . نیرو در هر بخش S مکعب باید نیروهای اعمال شده در زیر بخش را متعادل کند. در سه بخش نشان داده شده ، نیروها F (بالا سمت راست) ، F هستند(پایین سمت چپ) ، و (سمت راست پایین)؛ و مساحت S است ،و الف، به ترتیب. از اینرو، در سراسر S است F / در هر سه مورد.

نوع ساده دیگر تنش هنگامی اتفاق می افتد که بدن از هر جهت تحت فشار یا کشش برابر باشد. به عنوان مثال ، در بخشی از مایع یا گاز در حالت استراحت ، چه در بعضی از ظرف ها محصور باشد و چه به عنوان بخشی از توده بزرگتر مایعات ، این مورد وجود دارد. یا در داخل مکعبی از ماده الاستیک که توسط نیروهای عمود برابری به هر شش صورت فشار داده می شود یا کشیده می شود - به شرطی که در هر دو حالت ماده همگن باشد ، بدون تنش داخلی ، و تأثیر گرانش و سایر نیروهای خارجی قابل غفلت است.

در این شرایط ، تنش در هر سطح داخلی خیالی از نظر اندازه مساوی است و همیشه به طور عمود به سطح مستقل از جهت گیری سطح هدایت می شود. این نوع استرس را می توان ایزوتروپیک طبیعی یا فقط ایزوتروپیک نامید . اگر فشاری باشد فشار هیدرواستاتیک یا فقط فشار نامیده می شود . گازها بر اساس تعریف نمی توانند تنش های کششی را تحمل کنند ، اما برخی مایعات ممکن است تحت برخی شرایط مقادیر زیادی تنش کششی ایزوتروپیک را تحمل کنند. به لوله Z مراجعه کنید .

تنش های سیلندر [ ویرایش ]

قطعات با تقارن چرخشی مانند چرخ ، محور ، لوله و ستون در مهندسی بسیار رایج است. غالباً الگوهای تنشی دارای تقارن چرخشی یا حتی استوانه ای هستند . تجزیه و تحلیل چنین تنش های استوانه ای می تواند با استفاده از تقارن ، بعد دامنه و / یا تنسور تنش را کاهش دهد.

استرس عمومی [ ویرایش ]

اغلب ، اجسام مکانیکی همزمان بیش از یک نوع تنش را تجربه می کنند. این استرس ترکیبی نامیده می شود . در تنش نرمال و برشی ، شدت تنش برای سطوحی که عمود بر جهت خاصی هستند بیشترین است، و در هر سطحی که موازی با آن باشد صفر است . وقتی تنش برشی فقط در سطحهایی که عمود بر یک جهت خاص هستند صفر باشد ، تنش دو محوری نامیده می شود و می توان آن را به عنوان مجموع دو تنش طبیعی یا برشی مشاهده کرد. در عمومی ترین حالت ، تنش سه محوری نامیده می شود ، تنش در تمام عناصر سطحی غیر صفر است.

سنسور تنش کوشی[ ویرایش ]

مقاله اصلی: تانسور استرس کوشی

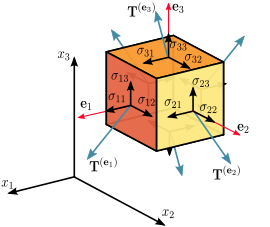
اجزای تنش در سه بعد

تصویربرداری تنشهای معمولی (پیکان ها) از طریق عناصر مختلف سطح در مرز یک ذره (کره) ، در یک ماده همگن تحت تنش سه محوری یکنواخت (اما نه ایزوتروپیک). تنش های طبیعی در محورهای اصلی 5+ ، 2+ و −3 واحد است.

تنش های ترکیبی را نمی توان با یک بردار توصیف کرد. حتی اگر مواد در کل حجم بدن به همان شکل تحت فشار قرار بگیرند ، فشار در هر سطح خیالی به جهت آن سطح ، به روشی غیر پیش پا افتاده بستگی خواهد داشت.

با این حال ، کوشی مشاهده کرد که بردار تنش استدر طول یک سطح همیشه یک تابع خطی از بردار طبیعی سطح وجود خواهد داشت ، بردار طول واحد که عمود بر آن است. به این معنا که،پ، که در آن تابع  راضی می کند

برای هر بردار  و هر عدد واقعی . کارکردکه اکنون تانسور تنش (کوشی) نامیده می شود ، کاملاً وضعیت تنش بدن تحت فشار یکنواخت را توصیف می کند. (امروزه ، هرگونه ارتباط خطی بین دو مقدار بردار فیزیکی ، تنسور نامیده می شود ، که نشان دهنده کاربرد اصلی کوشی برای توصیف "تنش ها" (تنش ها) در یک ماده است.) در حساب تنسور ،به عنوان تانسور مرتبه دوم از نوع (0،2) طبقه بندی می شود .

مانند هر نقشه خطی بین بردارها ، سنسور تنش را می توان در هر سیستم مختصات دکارتی انتخاب شده توسط یک ماتریس 3 × 3 از اعداد واقعی نشان داد. بستگی به شماره گذاری مختصات دارد یا نامگذاری شده ، ممکن است ماتریس به صورت زیر نوشته شود

 یا 

بردار تنشدر سطح با بردار نرمال (که متغیر است - "ردیف ؛ افقی" - بردار) با مختصات سپس یک محصول ماتریسی است (که در آن T در شاخص فوقانی است و تاخر ، و به عنوان یک نتیجه ما هموردا (ردیف) بردار) (نگاه در تانسور تنش کوشی )، این است که

رابطه خطی بین  و از قوانین اساسی حفظ مومنت خطی و تعادل ایستا نیروها پیروی می کند ، بنابراین از نظر ریاضی دقیق است ، برای هر ماده و هر شرایط تنش. اجزای سنسور تنش کوشی در هر نقطه از ماده ، معادلات تعادل را برآورده می کنند ( معادلات حرکت کوشی برای شتاب صفر). علاوه بر این ، اصل حفظ حرکت زاویه ای متضمن این است که تنسور تنش متقارن است ، یعنی، ، و . بنابراین ، وضعیت تنش محیط در هر نقطه و لحظه را می توان فقط با شش پارامتر مستقل و نه 9 تعیین کرد. اینها ممکن است نوشته شود

که در آن عناصرمی به نام تنش نرمال متعامد (نسبت به انتخاب دستگاه مختصات) و{تنش برشی متعامد .

تغییر مختصات [ ویرایش ]

سنسور تنش کوشی با تغییر در سیستم مختصات از قانون تبدیل تنسور پیروی می کند. نمایش گرافیکی این قانون تحول ، دایره توزیع تنش Mohr است .

به عنوان یک ماتریس 3 × 3 متقارن واقعی ، تانسور تنش دارای سه بردار ویژه متقابل طول واحد است و سه ارزش ویژه واقعی ، به طوری که . بنابراین ، در یک سیستم مختصات با محورها، تنسور تنش یک ماتریس مورب است و فقط سه جز normal عادی دارد تنش های اصلی . اگر سه مقدار ویژه برابر باشد ، تنش یک فشار یا کشش ایزوتروپیک است ، همیشه عمود بر هر سطح ، هیچ تنش برشی وجود ندارد ، و تنسور یک ماتریس مورب در هر قاب مختصات است.

استرس به عنوان یک میدان کششی [ ویرایش ]

به طور کلی ، استرس به طور یکنواخت روی بدن جسم توزیع نمی شود و ممکن است با توجه به زمان متفاوت باشد. بنابراین، تانسور تنش باید برای هر نقطه و هر لحظه تعریف شود، با در نظر گرفتن بینهایت کوچک ذرات محیط اطراف آن نقطه، و در نظر گرفتن تنش متوسط در آن ذرات به عنوان تنش در نقطه.

استرس در صفحات نازک [ ویرایش ]

یک ماشین مخزن ساخته شده از صفحات فولادی خم و جوش داده شده.

اشیا made ساخته شده توسط بشر معمولاً از صفحات مختلف مواد مختلف به وسیله عملیاتی ساخته می شوند که شخصیت آنها اساساً دو بعدی تغییر نمی کند ، مانند برش ، سوراخکاری ، خم شدن ملایم و جوشکاری در امتداد لبه ها. توصیف تنش در چنین اجسامی را می توان با مدل سازی آن قسمت ها به عنوان سطوح دو بعدی و نه اجسام سه بعدی ، ساده کرد.

در این دیدگاه ، یک "ذره" دوباره تعریف می شود به عنوان یک تکه ناچیز از سطح صفحه ، بنابراین مرز بین ذرات مجاور به یک عنصر خط بی نهایت کوچک تبدیل می شود. هر دو به طور ضمنی در بعد سوم گسترش می یابد ، طبیعی (از طریق) صفحه. سپس "تنش" به عنوان مقیاسی از نیروهای داخلی بین دو "ذره" مجاور در سرتاسر عنصر خط مشترک آنها ، تقسیم بر طول آن خط ، دوباره تعریف می شود. برخی از اجزای سنسور تنش را نمی توان نادیده گرفت ، اما از آنجا که ذرات در بعد سوم بی نهایت نیستند ، بنابراین نمی توان گشتاوری را که یک ذره در همسایگان خود اعمال می کند ، نادیده گرفت. این گشتاور به عنوان یک فشار خمشی مدل سازی می شود که تمایل به تغییر انحنا داردبشقاب با این حال ، این ساده سازی ها ممکن است در جوش ها ، در خمیدگی ها و چین های تیز (جایی که شعاع انحنا با ضخامت صفحه قابل مقایسه است) ، قابل تحمل نباشد .

تنش در تیرهای نازک [ ویرایش ]

برای مدل سازی تنش ، یک قطب ماهیگیری ممکن است یک بعدی در نظر گرفته شود.

تجزیه و تحلیل تنش را می توان به طور قابل ملاحظه ای برای میله های نازک ، تیرها یا سیم های یکنواخت (یا متغیر هموار) و مقطع عرضی که تحت خمش و پیچ خوردگی متوسط ​​قرار دارند ، ساده کرد. برای آن اجسام ، می توان فقط مقاطع عرضی عمود بر محور میله را در نظر گرفت و "ذره" را دوباره تعریف کرد که به عنوان یک قطعه سیم با طول بینهایت کوچک بین دو مقطع چنین است. تنش معمولی سپس به یک اسکالر کاهش می یابد (کشش یا فشرده سازی میله) ، اما باید تنش خمشی (که سعی دارد انحنای میله را در جهتی عمود بر محور تغییر دهد) و تنش پیچشی را نیز در نظر بگیریم ( که سعی دارد آن را در مورد محور خود بپیچاند یا از حالت پیچش خارج کند).

سایر توصیفات استرس [ ویرایش ]

تنسور تنش کوشی برای تجزیه و تحلیل تنش در اجسام مادی که دچار تغییر شکل های کوچک می شوند ، مورد استفاده قرار می گیرد که در این موارد اختلاف در توزیع تنش را می توان نادیده گرفت. برای تغییر شکلهای بزرگ ، که تغییر شکل محدود نیز نامیده می شود ، سایر اقدامات تنش ، مانند سنسورهای تنش استرس Piola-Kirchhoff اول و دوم ، تنش تنش Biot و تنش تنش Kirchhoff مورد نیاز است.

جامدات ، مایعات و گازها دارای زمینه های تنش هستند . مایعات استاتیک از فشار طبیعی پشتیبانی می کنند اما تحت تنش برشی جریان می یابند . حرکت مایعات چسبناک می تواند از فشار برشی (فشار دینامیکی) پشتیبانی کند. جامدات می توانند هم از فشار برشی و هم از تنش طبیعی پشتیبانی کنند ، با مواد شکل پذیر در اثر برش از کار می افتند و مواد شکننده نیز تحت تنش طبیعی از بین می روند. همه مواد دارای تغییرات وابسته به دما در خصوصیات مربوط به تنش هستند و مواد غیر نیوتنی نیز دارای تغییرات وابسته به سرعت هستند.

شیشه مقاوم در برابر شیشه عقب ماشین. تغییرات در تنش شیشه ای به وضوح دیده می شود که از طریق فیلتر قطبی عکس گرفته شود (تصویر پایین).

تحلیل استرس [ ویرایش ]

تحلیل تنش شاخه ای از فیزیک کاربردی است که تعیین توزیع داخلی نیروهای داخلی در اجسام جامد را پوشش می دهد. این یک ابزار اساسی در مهندسی برای مطالعه و طراحی سازه هایی مانند تونل ها ، سدها ، قطعات مکانیکی و اسکلت های سازه ای تحت بارهای تعیین شده یا مورد انتظار است. این در بسیاری از رشته های دیگر نیز مهم است. به عنوان مثال ، در زمین شناسی ، برای مطالعه پدیده هایی مانند تکتونیک صفحه ، آتش فشانی و بهمن . و در زیست شناسی ، آناتومی موجودات زنده را درک کنید.

اهداف و مفروضات [ ویرایش ]

تجزیه و تحلیل استرس به طور کلی مربوط به اشیا objects و ساختارهایی است که می توان در تعادل ایستای ماکروسکوپی فرض کرد . طبق قوانین حرکت نیوتن ، هرگونه نیروی خارجی که به چنین سیستمی وارد می شود باید توسط نیروهای واکنش داخلی متعادل شود ، [11] : ص 97 که تقریباً همیشه نیروهای تماس سطحی بین ذرات مجاور هستند - یعنی تنش. [5] از آنجا که هر ذره ای نیاز به تعادل دارد ، این تنش واکنش به طور کلی از ذره ای به ذره انتشار می یابد و باعث ایجاد توزیع تنش در بدن می شود.

مشکل معمول در تحلیل تنش ، تعیین این تنشهای داخلی با توجه به نیروهای خارجی است که بر روی سیستم وارد می شوند. حالت دوم ممکن است نیروهای بدنی (مانند نیروی جاذبه یا جاذبه مغناطیسی) باشد که در کل حجم ماده عمل می کنند. [12] : p.42–81 یا بارهای متمرکز (مانند اصطکاک بین محور و یاطاقان ، یا وزن چرخ قطار روی ریل) ، که تصور می شود در یک منطقه دو بعدی یا در امتداد یک خط ، یا در یک نقطه واحد.

در تجزیه و تحلیل تنش به طور معمول دلایل فیزیکی نیروها یا ماهیت دقیق مواد را نادیده می گیرد. در عوض ، فرض می شود که تنش ها با معادلات سازه ای شناخته شده به تغییر شکل (و در مسائل غیر استاتیکی ، با سرعت تغییر شکل) مواد مربوط می شوند . [13]