تعریف سطح حاکم: هر نقطه روی یک خط قرار دارد

در هندسه ، یک سطح S است حکومت (همچنین به نام اسکرول ) اگر از طریق هر نقطه از S است یک خط مستقیم وجود دارد نهفته است که در S . مثالها عبارتند از فضا ، سطح جانبی یک استوانه و یا مخروط ، یک سطح مخروطی با بیضوی هادی از مخروطی شکل سمت راست ، به پیچوار و قابل توسعه مماس از صاف منحنی در فضا است.

یک سطح حاکم را می توان مجموعه نقاطی که توسط یک خط مستقیم متحرک جارو می شوند ، توصیف کرد. به عنوان مثال ، یک مخروط با ثابت نگه داشتن یک نقطه از یک خط در حالی که یک نقطه دیگر را در امتداد دایره حرکت می دهد ، تشکیل می شود . اگر از طریق هر نقطه از آن دو خط مجزا وجود داشته باشد که روی سطح قرار داشته باشد ، یک سطح دوبرابر می شود. قطع مخروطی هذلولی و hyperboloid از یک ورق مضاعف حکومت سطوح. هواپیما تنها سطحی است که از طریق هر یک از نقاط خود شامل حداقل سه خط مشخص است ( Fuchs & Tabachnikov 2007 ).

خصوصیات حاکم یا مضاعف بودن توسط نقشه های تصویری حفظ می شود ، بنابراین مفاهیم هندسه فرافکنی هستند . در هندسه جبری گاهی اوقات سطوح حاکم به عنوان سطوحی در فضای افقی یا تصویری بیش از یک میدان در نظر گرفته می شوند ، اما همچنین گاهی اوقات آنها به عنوان سطوح انتزاعی جبری بدون تعبیه در فضای افقی یا تصویری در نظر گرفته می شوند ، در این حالت به معنای "خط مستقیم" است یک خط افقی یا تصویری

 

فهرست

تعریف و نمایش پارامتری [ ویرایش ]

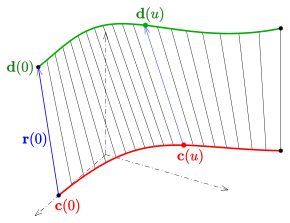
سطح حاکم تولید شده توسط دو منحنی Bézier به عنوان مدیر (قرمز ، سبز)

منیفولد دو بعدی متمایز ، در صورت اتحاد یک خانواده از خطوط یک پارامتر ، سطح حاکم نامیده می شود . خطوط این خانواده مولدهای سطح حاکم هستند.

یک سطح حاکم را می توان با نمایش پارامتریک فرم توصیف کرد

  • {\ displaystyle \ quad \ mathbf {x} (u، v) = {\ color {red} \ mathbf {c} (u)} + v \؛ {\ color {blue} \ mathbf {r} (u)} \ ، \ v \ in \ mathbb {R} \،}.

هر منحنی {\ displaystyle \؛ v \ mapsto \ mathbf {x} (u_ {0}، v) \؛} با پارامتر ثابت  u = u_0 یک ژنراتور (خط) و منحنی است {\ displaystyle \؛ u \ mapsto \ mathbf {c} (u) \؛}است هادی از نمایندگی. بردارها{\ displaystyle \؛ \ mathbf {r} (u) \ neq {\ bf {0 \؛}}} جهت های ژنراتورها را توصیف کنید.

Directrix ممکن است به یک نقطه سقوط کند (در صورت مخروط ، به مثال زیر مراجعه کنید).

متناوباً سطح حاکم (CR) را می توان با توصیف کرد

  • {\ displaystyle \ quad \ mathbf {x} (u، v) = (1-v) \؛ {\ color {red} \ mathbf {c} (u)} + v \؛ {\ color {green} \ mathbf {d} (تو)} \}

با دایرکتریکس دوم {\ displaystyle \؛ \ mathbf {d} (u) = \ mathbf {c} (u) + \ mathbf {r} (u) \؛}.

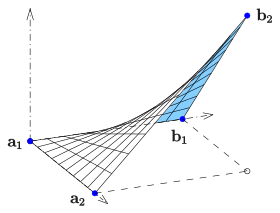
متناوباً ، می توان با دو منحنی غیر متقاطع شروع کرد {\ displaystyle \ mathbf {c} (u) ، \ mathbf {d} (u)}به عنوان مدیر ، و توسط (CD) یک سطح حاکم با جهت خط دریافت کنید{\ displaystyle \؛ \ mathbf {r} (u) = \ mathbf {d} (u) - \ mathbf {c} (u) \.}

برای تولید یک سطح حاکم توسط دو دایرکتوری (یا یک دایرکتریکس و بردارهای جهت) نه تنها شکل هندسی این منحنی ها ضروری است بلکه نمایش های پارامتری خاص آنها نیز بر شکل سطح حاکم تأثیر می گذارد (به نمونه های a نگاه کنید) ) ، د))

برای تحقیقات نظری ، نمایندگی (CR) از مزیت بیشتری برخوردار است ، زیرا این پارامتر استv فقط یک بار ظاهر می شود

مثالها [ ویرایش ]

سیلندر ، مخروط

استوانه دایره ای سمت راست [ ویرایش ]

{\ displaystyle \ x ^ {2} + y ^ {2} = a ^ {2} \}:

{\ displaystyle \ mathbf {x} (u، v) = (a \ cos u، a \ sin u، v) ^ {T}}

{\ displaystyle = {\ color {red} (a \ cos u، a \ sin u، 0) ^ {T}} \؛ + \؛ v \؛ {\ color {blue} (0،0،1) ^ {T}}}

{\ displaystyle = (1-v) \؛ {\ color {red} (a \ cos u، a \ sin u، 0) ^ {T}} \؛ + \؛ v \؛ {\ color {green} ( a \ cos u، a \ sin u، 1) ^ {T}} \.}

با

{\ displaystyle \ mathbf {c} (u) = (a \ cos u، a \ sin u، 0) ^ {T} \، \ \ mathbf {r} (u) = (0،0،1) ^ { T} \ ، \ \ mathbf {d} (u) = (a \ cos u ، a \ sin u، 1) ^ {T} \.}

مخروط دایره ای راست [ ویرایش ]

{\ displaystyle \ x ^ {2} + y ^ {2} = z ^ {2} \}:

{\ displaystyle \ mathbf {x} (u، v) = (\ cos u، \ sin u، 1) ^ {T} \؛ + \؛ v \؛ (\ cos u، \ sin u، 1) ^ { T}}

{\ displaystyle = (1-v) \؛ (\ cos u، \ sin u، 1) ^ {T} \؛ + \؛ v \؛ (2 \ cos u، 2 \ sin u، 2) ^ {T }.}

{\ displaystyle \ quad \ mathbf {c} (u) = (\ cos u، \ sin u، 1) ^ {T} \؛ = \؛ \ mathbf {r} (u) \، \ quad \ mathbf {d } (u) = (2 \ cos u، 2 \ sin u، 2) ^ {T} \.}
در این حالت می توان از راس به عنوان دایرکتریکس استفاده کرد ، یعنی: {\ displaystyle \ \ mathbf {c} (u) = (0،0،0) ^ {T} \} و {{\ displaystyle \ \ mathbf {r} (u) = (\ cos u، \ sin u، 1) ^ {T} \} به عنوان خطوط

برای هر مخروط می توان اوج را به عنوان دایرکتریکس انتخاب کرد. این حالت نشان می دهد: دایرکتریکس یک سطح حاکم ممکن است تا یک نقطه منحط شود .

هلیکوئید

هلیکوئید [ ویرایش ]

{\ displaystyle \ mathbf {x} (u، v) = \؛ (v \ cos u، v \ sin u، ku) ^ {T} \؛}

{\ displaystyle = \؛ (0،0 ، ku) ^ {T} \؛ + \؛ v \؛ (\ cos u، \ sin u، 0) ^ {T} \}

{\ displaystyle = \؛ (1-v) \؛ (0،0، ku) ^ {T} \؛ + \؛ v \؛ (\ cos u، \ sin u، ku) ^ {T} \.}

دایرکتریکس{\ displaystyle \ \ mathbf {c} (u) = (0،0 ، ku) ^ {T} \؛} محور z است ، جهت های خط هستند {\ displaystyle \؛ \ mathbf {r} (u) = \ (\ cos u، \ sin u، 0) ^ {T} \؛} و دایرکتریکس دوم {\ displaystyle \ \ mathbf {d} (u) = (\ cos u، \ sin u، ku) ^ {T} \}یک مارپیچ .

هلیکوئید یک مورد خاص از هلیکوئیدهای تعمیم یافته حاکم است .

سیلندر ، مخروط و هیپربلوئید [ ویرایش ]

hyperboloid از یک ورق برای{\ displaystyle \ varphi = 63 ^ {\ circ}}

نمایش پارامتری

{\ displaystyle \ mathbf {x} (u، v) = (1-v) \؛ (\ cos (u- \ varphi) ، \ sin (u- \ varphi) ، - 1) ^ {T} \؛ + \؛ v \؛ (\ cos (u + \ varphi) ، \ sin (u + \ varphi) ، 1) ^ {T}}

دارای دو دایره افقی به عنوان مدیر است. پارامتر اضافی\ varphi اجازه می دهد تا نمایش پارامتری دایره ها تغییر کند. برای

{\ displaystyle \ varphi = 0 \} یکی استوانه را می گیردx ^ {2} + y ^ {2} = 1، برای

{\ displaystyle \ varphi = \ pi / 2 \} یکی مخروط را بدست می آورد x ^ {2} + y ^ {2} = z ^ {2} و برای

{\ displaystyle 0 <\ varphi <\ pi / 2 \} یکی با معادله یک ابرقهرمان از یک ورق بدست می آورد {\ displaystyle \ {\ tfrac {x ^ {2} + y ^ {2}} {a ^ {2}}} - {\ tfrac {z ^ {2}} {c ^ {2}}} = 1 \ } و نیمه محورها {\ displaystyle \ a = \ cos \ varphi \؛ ، \؛ c = \ cot \ varphi}.

هیپربلویید از یک ورق یک سطح دو برابر حاکم است.

پارابولویید هذلولی

پارابولویید هذلولی [ ویرایش ]

اگر دو کارگردان در (CD) خط باشند

{\ displaystyle \ mathbf {c} (u) = (1-u) \ mathbf {a} _ {1} + u \ mathbf {a} _ {2} ، \ quad \ mathbf {d} (u) = ( 1-u) \ mathbf {b} _ {1} + u \ mathbf {b} _ {2}}

یکی می شود

{\ displaystyle \ mathbf {x} (u، v) = (1-v) {\ big (} (1-u) \ mathbf {a} _ {1} + u \ mathbf {a} _ {2} { \ big)} \ + \ v {\ big (} (1-u) \ mathbf {b} _ {1} + u \ mathbf {b} _ {2} {\ big)} \}،

که همان پارابولویید هذلولی است که 4 نقطه را درون یابی می کند{\ displaystyle \ \ mathbf {a} _ {1} ، \؛ \ mathbf {a} _ {2} ، \؛ \ mathbf {b} _ {1} ، \؛ \ mathbf {b} _ {2} \ }بصورت دو خطی [1]

بدیهی است که سطح حاکم یک سطح دوبرابر است ، زیرا هر نقطه روی دو خط سطح قرار دارد.

برای مثال نشان داده شده در نمودار:

{\ displaystyle \ \ mathbf {a} _ {1} = (0،0،0) ^ {T} ، \؛ \ mathbf {a} _ {2} = (1،0،0) ^ {T} ، \؛ \ mathbf {b} _ {1} = (0،1،0) ^ {T} ، \؛ \ mathbf {b} _ {2} = (1،1،1) ^ {T} \}.

پارابولویید هذلولی دارای معادله است {\ displaystyle z = xy}.

نوار موبیوس

نوار موبیوس [ ویرایش ]

سطح حاکم

{\ displaystyle \ mathbf {x} (u، v) = \ mathbf {c} (u) + v \؛ \ mathbf {r} (u)}

با

{\ displaystyle \ mathbf {c} (u) = (\ cos 2u ، \ sin 2u ، 0) ^ {T} \} (دایره به عنوان دایرکتریکس) ،

{\ displaystyle \ mathbf {r} (u) = (\ cos u \ cos 2u ، \ cos u \ sin 2u ، \ sin u) ^ {T} \ ، \ quad 0 \ leq u <\ pi \،}

حاوی نوار موبیوس است.

نمودار نوار موبیوس را برای نشان می دهد {\ displaystyle -0.3 \ leq v \ leq 0.3}.

یک محاسبه ساده نشان می دهد{\ displaystyle \ det (\ mathbf {\ dot {c}} (0) \؛ ، \؛ \ mathbf {\ dot {r}} (0) \؛ ، \؛ \ mathbf {r} (0)) \ ؛ \ neq \؛ 0 \}(بخش بعدی را ببینید). از این رو تحقق بخشیده شده از نوار موبیوس قابل توسعه نیست . اما نوارهای موبیوس قابل توسعه وجود دارد. [2]

منبع

https://en.wikipedia.org/wiki/Ruled_surface