تفسیر بصری [ ویرایش ]

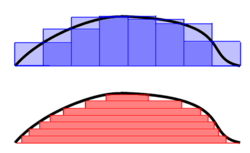
ادغام ریمان-داربوکس (به رنگ آبی) و ادغام لبسگ (با رنگ قرمز).

برای درک شهودی درباره رویکردهای مختلف ادغام ، تصور کنیم که می خواهیم حجم کوهی (بالاتر از سطح دریا) را پیدا کنیم.

رویکرد ریمان - داربو

پایه کوه را به شبکه ای از مربع های 1 متری تقسیم کنید. ارتفاع کوه را در مرکز هر میدان اندازه بگیرید. حجم بر روی یک مربع شبکه واحد حدود 1 متر است 2 × (ارتفاع آن مربع است)، بنابراین حجم کل 1 متر است 2 برابر مجموع ارتفاعات.

رویکرد Lebesgue

یک نقشه کانتور از کوه ترسیم کنید ، جایی که خطوط مجاور 1 متر از یکدیگر فاصله دارند. حجم زمین یک کانتور منفرد تقریباً 1 متر مربع است (مساحت آن کانتور) ، بنابراین حجم کل حاصل جمع این مناطق برابر با 1 متر است.

Folland خلاصه تفاوت بین ریمان و Lebesgue روش کند: «برای محاسبه انتگرال ریمان F ، یکی پارتیشن دامنه [ ، ب ] به subintervals"، در حالی که در انتگرال Lebesgue، "یکی در اثر پارتیشن بندی وسیعی از F " [1]

به سمت یک تعریف رسمی [ ویرایش ]

یک عملکرد قابل اندازه گیری همراه با مجموعه نشان داده شده است {\ displaystyle \ {x: f (x)> t \}}(در محور x ). انتگرال Lebesgue با برش دادن در محور- y با استفاده از اندازه گیری 1 بعدی Lebesgue برای اندازه گیری "عرض" برش ها بدست می آید.

برای تعریف انتگرال Lebesgue نیاز به مفهوم رسمی اندازه گیری است که تقریباً به هر مجموعه A از اعداد واقعی یک عدد غیر منفی μ ( A ) را نشان می دهد که نشان دهنده "اندازه" A است . این مفهوم "اندازه" باید با طول معمول یک فاصله یا اتحاد جداگانه فواصل مطابقت داشته باشد. فرض کنید f  : ℝ → ℝ + یک تابع با ارزش واقعی غیر منفی است. با استفاده از فلسفه "تقسیم دامنه f " ، انتگرال f باید مجموع بیش از t منطقه ابتدایی موجود در نوار افقی نازک بین y = t باشدو y = t - dt . این منطقه ابتدایی فقط است

\ mu \ چپ (\ {x \ وسط f (x)> t \} \ راست) \ ، dt.

اجازه دهید

f ^ {*} (t) = \ mu \ چپ (\ {x \ mid f (x)> t \} \ راست).

انتگرال Lebesgue از f توسط [2] تعریف می شود

\ int f \، d \ mu = \ int _ {0} ^ {\ infty} f ^ {*} (t) \، dt

جایی که انتگرال در سمت راست یک انتگرال معمولی نامناسب ریمان است . توجه داشته باشید که F * غیر منفی کاهش عملکرد است، و در نتیجه تا جدایی ناپذیر ریمان نامناسب به خوبی تعریف شده با ارزش در فاصله [0، ∞] . برای یک کلاس مناسب از توابع ( توابع قابل اندازه گیری ) ، این انتگرال Lebesgue را تعریف می کند.

یک عملکرد قابل اندازه گیری عمومی (نه لزوماً مثبت) f قابل تجزیه Lebesgue است اگر فضای بین نمودار f و x-x محدود باشد:

\ int | f | \ ، d \ mu <+ \ بی اعتبار است.

در آن حالت ، همانند مورد ریمانیان ، انتگرال تفاوت بین ناحیه بالای x- axis و ناحیه زیر x- axis است:

\ int f \، d \ mu = \ int f ^ {+} \، d \ mu - \ int f ^ {-} \، d \ mu

جایی که f = f ^ {+} - f ^ {-}تجزیه f به اختلاف دو تابع غیر منفی داده شده توسط است

{\ displaystyle {\ start {linjë ) ، & {\ text {if}} f (x)> 0 ، \\ 0 و {\ text {در غیر این صورت}} \ end {موارد}} \\ f ^ {-} (x) & = \ max \ {-f (x) ، 0 \} و {} = {} و {\ {شروع {موارد} -f (x) ، و {\ text {if}} f (x) <0 ، \\ 0 و { \ text {در غیر این صورت.}} \ end {موارد}} \ end {تراز شده}}}

ساخت و ساز [ ویرایش ]

نظریه انتگرال Lebesgue به نظریه ای از مجموعه ها و اندازه گیری های قابل اندازه گیری روی این مجموعه ها و همچنین تئوری توابع و انتگرال های قابل اندازه گیری درباره این توابع نیاز دارد.

نظریه اندازه گیری [ ویرایش ]

اطلاعات بیشتر: اندازه گیری (ریاضیات)

نظریه اندازه گیری در ابتدا برای ارائه انتزاعی مفید از مفهوم طول زیر مجموعه های خط واقعی - و به طور کلی ، مساحت و حجم زیر مجموعه های فضاهای اقلیدسی ایجاد شد. به طور خاص ، این یک پاسخ سیستماتیک به این سوال ارائه می دهد که کدام زیر مجموعه های provided دارای طول هستند. همانطور که بعداً تحولات تئوری مجموعه نشان داد (به مجموعه غیرقابل اندازه گیری مراجعه کنید ) ، اختصاص دادن طول به همه زیرمجموعه های impossible به گونه ای که برخی از خصوصیات افزودنی طبیعی و عدم تغییر ترجمه را حفظ کند غیرممکن است. این نشان می دهد که انتخاب یک کلاس مناسب از زیر مجموعه های قابل اندازه گیری یک پیش نیاز اساسی است.

انتگرال ریمان به وضوح از مفهوم طول استفاده می کند. در واقع ، عنصر محاسبه برای انتگرال ریمان مستطیل [ a ، b ] × [ c ، d ] است که مساحت آن برابر با ( b - a ) ( d - c ) است . مقدار b - a طول قاعده مستطیل و d - c ارتفاع مستطیل است. ریمان فقط می توانست از مستطیل های مسطح برای تخمین مساحت زیر منحنی استفاده کند ، زیرا تئوری کافی برای اندازه گیری مجموعه های کلی تر وجود نداشت.

در توسعه نظریه در اکثر کتابهای درسی مدرن (پس از سال 1950) ، روش اندازه گیری و ادغام بدیهی است . این به این معنی است که اندازه گیری هر تابعی μ است که در کلاس خاصی از مجموعه های X  مجموعه ای E تعریف شده باشد ، که لیست خاصی از خصوصیات را برآورده می کند. می توان نشان داد که این خصوصیات در موارد مختلف نگهداری می شوند.

توابع قابل اندازه گیری [ ویرایش ]

ما با یک فضای اندازه گیری ( E ، X ، μ) شروع می کنیم که در آن E یک مجموعه است ، X یک جبر σ از زیر مجموعه های E است ، و μ یک اندازه گیری (غیر منفی ) در E است که روی مجموعه های X تعریف شده است .

به عنوان مثال، E می تواند اقلیدسی N فضا- ℝ N و یا برخی از لبسگو اندازه گیری زیر مجموعه ای از آن، X است σ جبر از همه لبسگو زیر مجموعه های اندازه گیری الکترونیکی و μ اندازه گیری لبسگو است. در تئوری احتمالات ریاضی ، ما مطالعه خود را به اندازه گیری  احتمال μ محدود می کنیم ، که μ ( E ) = 1 را برآورده می کند .

نظریه لبسگ انتگرال ها را برای دسته ای از توابع به نام توابع قابل اندازه گیری تعریف می کند . یک تابع با ارزش واقعی f در E قابل اندازه گیری است اگر پیش تصویری از هر بازه از فرم ( t ، ∞) (در واقع ، هر مجموعه Borel ) در X باشد :

{\ displaystyle \ {x \، \ mid \، f (x)> t \} \ in X \ quad \ forall t \ in \ mathbb {R}.}

ما می توانیم نشان دهیم که این مساوی با الزام به پیش نمایش تصویر زیر مجموعه های Borel از in در X است . مجموعه توابع قابل اندازه گیری تحت عملیات جبری بسته می شود ، اما مهمتر از آن در انواع مختلف محدودیت های متوالی نقطه ای بسته می شود :

\ sup _ {k \ in \ mathbb {N}} f_ {k} ، \ quad \ liminf _ {k \ in \ mathbb {N}} f_ {k} ، \ quad \ limsup _ {k \ in \ mathbb { N}} f_ {k}

اگر توالی اصلی ( f k ) k ، جایی که k ∈ of ، شامل توابع قابل اندازه گیری است ، قابل اندازه گیری هستند.

روشهای مختلفی برای تعریف انتگرال وجود دارد:

{\ displaystyle \ int _ {E} f \، d \ mu = \ int _ {E} f \ چپ (x \ راست) \، d \ mu \ چپ (x \ راست)}

برای توابع حقیقی اندازه گیری F در تعریف E .

ساخت انتگرال [ ویرایش ]

تقریب یک عملکرد با توابع ساده.

یک روش برای ساخت انتگرال Lebesgue استفاده از توابع به اصطلاح ساده است : ترکیبات خطی واقعی محدود از توابع نشانگر . برای یک مبتدی نظریه اندازه گیری ، این ساختار انتگرال Lebesgue هنگامی که با روش استفاده از مجموع ریمان با تعریف / ساخت انتگرال ریمان مقایسه می شود ، شهودی تر است . از توابع ساده می توان برای تقریب یک تابع قابل اندازه گیری ، با تقسیم دامنه به لایه ها ، استفاده کرد. انتگرال یک تابع ساده برابر است با اندازه گیری یک لایه داده شده ، چند برابر ارتفاع آن لایه. انتگرال یک عملکرد قابل اندازه گیری عمومی غیر منفی سپس به عنوان یک برتری مناسب تعریف می شودتقریب ها توسط توابع ساده ، و انتگرال یک تابع قابل اندازه گیری (نه لزوماً مثبت) تفاوت دو انتگرال از توابع قابل اندازه گیری غیر منفی است ، همانطور که قبلا ذکر شد .

توابع نشانگر [ ویرایش ]

برای اختصاص یک مقدار به انتگرال تابع نشانگر 1 S از یک مجموعه قابل اندازه گیری S سازگار با اندازه داده شده μ ، تنها انتخاب معقول این است که تنظیم کنید:

{\ displaystyle \ int 1_ {S} \، d \ mu = \ mu (S).}

توجه داشته باشید که نتیجه ممکن است برابر با + ∞ باشد ، مگر اینکه μ یک اندازه گیری محدود باشد.

توابع ساده [ ویرایش ]

ترکیبی خطی محدود از توابع نشانگر

\ sum _ {k} a_ {k} 1_ {S_ {k}}

که در آن ضرایب a k اعداد واقعی و S k مجموعه های قابل اندازه گیری جداگانه هستند ، یک تابع ساده قابل اندازه گیری نامیده می شود . انتگرال را با خطی بودن به توابع ساده قابل اندازه گیری غیر منفی گسترش می دهیم . وقتی ضرایب a k غیر منفی باشند ، تنظیم می کنیم

\ int \ چپ (\ sum _ {k} a_ {k} 1_ {S_ {k}} \ راست) \ ، d \ mu = \ sum _ {k} a_ {k} \ int 1_ {S_ {k}} \ ، d \ mu = \ sum _ {k} a_ {k} \ ، \ mu (S_ {k}).

قرارداد 0 × ∞ = 0 باید استفاده شود ، و نتیجه ممکن است بی نهایت باشد. حتی اگر یک تابع ساده از بسیاری جهات به عنوان ترکیبی خطی از توابع نشانگر قابل نوشتن باشد ، انتگرال همیشه یکسان است. این را می توان با استفاده از خاصیت افزودنی اندازه گیری ها نشان داد.

برخی از مراقبت مورد نیاز است هنگام تعریف جدایی ناپذیر از یک واقعی ارزش تابع ساده، برای جلوگیری از بیان تعریف نشده ∞ - ∞ : یکی فرض می شود که نمایندگی

f = \ sum _ {k} a_ {k} 1_ {S_ {k}}

به گونه ای است که μ ( S k ) <∞ هر زمان که k k ≠ 0 باشد. سپس فرمول فوق برای انتگرال f منطقی است ، و نتیجه به نمایندگی خاص f برآورده ساختن فرض ها بستگی ندارد .

اگر B زیر مجموعه قابل اندازه گیری است E و حال یک تابع ساده اندازه گیری است یکی را تعریف می کند

\ int _ {B} s \، d \ mu = \ int 1_ {B} \، s \، d \ mu = \ sum _ {k} a_ {k} \، \ mu (S_ {k} \ cap B )

توابع غیر منفی [ ویرایش ]

بگذارید f یک تابع قابل اندازه گیری غیر منفی در E باشد ، که به آن اجازه می دهیم مقدار + ain را بدست آوریم ، به عبارت دیگر ، f مقادیر غیر منفی را در خط عدد توسعه یافته واقعی می گیرد . ما تعریف می کنیم

\ int _ {E} f \، d \ mu = \ sup \ left \ {\، \ int _ {E} s \، d \ mu: 0 \ leq s \ leq f، \ s \ {\ text {simple }}\،\درست\}.

ما باید نشان دهیم که این انتگرال با یک توالی قبلی تعریف شده است ، که در مجموعه توابع ساده تعریف شده است ، زمانی که E   یک قطعه است [ a ،  b ]. همچنین این سال وجود دارد که آیا این امر به هیچ وجه با مفهوم ادغام ریمان مطابقت دارد؟ می توان ثابت کرد که پاسخ هر دو سوال مثبت است.

ما انتگرال f را برای هر تابع قابل اندازه گیری غیر واقعی منفی قابل اندازه گیری در  E تعریف کرده ایم . برای برخی از توابع ، این انتگرال ∫ E  f  dμ بی نهایت است.

داشتن یک توالی خاص از توابع ساده که تقریباً به خوبی با انتگرال Lebesgue (تقریباً به صورت یک مبلغ ریمان) تقریبی باشد ، بسیار مفید است. برای یک تابع غیر قابل اندازه گیری f ، اجازه دهید{\ displaystyle s_ {n} (x)} تابع ساده ای است که مقدار آن است {\ displaystyle k / 2 ^ {n}} هر زمان که {\ displaystyle k / 2 ^ {n} \ leq f (x) <(k + 1) / 2 ^ {n}}، برای k یک عدد صحیح غیر منفی کمتر از (بگویید)4 ^ {n}. سپس می توان مستقیماً ثابت کرد که

{\ displaystyle \ int f \، d \ mu = \ lim _ {n \ to \ infty} \ int s_ {n} \، d \ mu}

و این محدودیت در سمت راست به عنوان یک عدد واقعی گسترش یافته وجود دارد. این ارتباط بین رویکرد به انتگرال Lebesgue با استفاده از توابع ساده و انگیزه برای انتگرال Lebesgue با استفاده از یک پارتیشن از محدوده است.