ساختار درجه بندی شده [ ویرایش ]
محصول خارجی یک وکتور k با یک وکتور p یک وکتور ( k + p ) است که یک بار دیگر به دو قطبی بودن استناد می کند. در نتیجه ، تجزیه مستقیم مستقیم بخش قبل
به جبر خارجی ساختار اضافی جبر درجه بندی شده می دهد ، یعنی
علاوه بر این ، اگر K زمینه پایه باشد ، ما داریم

محصول خارجی ضد تغییر است ، به این معنی که اگر α ∈ Λ k ( V ) و β ∈ Λ p ( V ) ،
علاوه بر مطالعه ساختار درجه بندی شده در جبر خارجی ، Bourbaki (1989) ساختارهای درجه بندی شده اضافی را در جبرهای خارجی مانند نمونه هایی که در جبر خارجی یک ماژول درجه بندی شده (ماژولی که از قبل درجه بندی خاص خود را دارد) مطالعه می کند.
دارایی جهانی [ ویرایش ]
بگذارید V یک فضای بردار بیش از قسمت K باشد. به طور غیررسمی ، ضرب در Λ ( V ) با دستکاری نمادها و تحمیل قانون توزیعی ، قانون انجمنی و استفاده از هویت v ∧ v = 0 برای v ∈ V انجام می شود . به طور رسمی ، Λ ( V ) "عمومی ترین" جبر است که در آن قوانین برای ضرب وجود دارد ، به این معنا که هر جبر K انجمنی متحد حاوی V با ضرب متناوب در V باید یک تصویر همگن ازΛ ( V ) . به عبارت دیگر ، جبر خارجی دارای ویژگی جهانی زیر است : [10]
با توجه به هر unital انجمنی K جبر و هر گونه K - نقشه خطی J : V → به طوری که J ( V ) J ( V ) = 0 برای هر V در V ، پس از آن وجود دارد وجود دارد دقیقا یکی unital جبر همریخت F : Λ ( V ) → به طوری که J ( V ) = F ( من ( V )) برای همه V در V (در اینجا من شامل طبیعی بودن V در Λ ( V ) است ، به بالا مراجعه کنید).
برای ساختن عمومی ترین جبر که حاوی V است و ضرب آن در V متناوب است ، طبیعی است که با عمومی ترین جبر انجمنی حاوی V شروع شود ، جبر تنسور T ( V ) ، و سپس ویژگی متناوب را با گرفتن یک مناسب خارج قسمت . بنابراین I ایده آل دو طرفه را در T ( V ) تولید شده توسط تمام عناصر فرم v ⊗ v برای v در V می گیریم و Λ ( V ) را تعریف می کنیم به عنوان ضریب
(و از ∧ به عنوان نماد ضرب در Λ ( V ) استفاده کنید) . پس از آن ساده است که نشان می دهیم Λ ( V ) حاوی V است و خاصیت جهانی فوق را برآورده می کند.
به عنوان یک نتیجه از این ساخت و ساز ، عملیات اختصاص دادن به یک فضای بردار V جبر خارجی آن Λ ( V ) یک عامل تفریحی از دسته فضاهای برداری به دسته جبرها است.
به جای تعریف اول Λ ( V ) و سپس شناسایی نیروهای خارجی Λ k ( V ) به عنوان زیر فضاهای خاص ، می توان ابتدا فضاهای Λ k ( V ) را تعریف کرد و سپس آنها را با هم ترکیب کرد تا جبر Λ ( V ) تشکیل شود . این روش اغلب در هندسه دیفرانسیل استفاده می شود و در بخش بعدی شرح داده می شود.
تعمیم [ ویرایش ]
با توجه به یک حلقه جابجایی R و یک ماژول R - M ، ما می توانیم جبر خارجی Λ ( M ) را همانطور که در بالا گفته شد ، به عنوان ضریب مناسب جبر تنسور T ( M ) تعریف کنیم. این ویژگی جهانی مشابه را برآورده خواهد کرد. بسیاری از خصوصیات Λ ( M ) نیز مستلزم آن است که M یک ماژول فرافکنی باشد . که در آن ابعاد محدود استفاده شده است، خواص بیشتر نیاز دارند که M شود finitely ایجاد و تصویری. تعمیم در مورد شایع ترین شرایط را می توان در بورباکی (1989) یافت .
جبرهای بیرونی بسته نرم افزاری بردارها اغلب در هندسه و توپولوژی در نظر گرفته می شوند. هیچ تفاوتی اساسی بین خصوصیات جبری جبر خارجی بسته های برداری محدود بعدی و جبر خارجی ماژول های پروژه ای تولید شده با محدودیت وجود ندارد ، توسط قضیه Serre-Swan . بیشتر جبری بیرونی طور کلی می توان برای تعریف قرقره از ماژول.
منبع
منبع
https://en.wikipedia.org/wiki/Exterior_algebra
https://en.wikipedia.org/wiki/Exterior_algebra




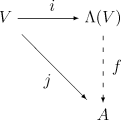

 در این وبلاگ به ریاضیات و کاربردهای آن و تحقیقات در آنها پرداخته می شود. مطالب در این وبلاگ ترجمه سطحی و اولیه است و کامل نیست.در صورتی سوال یا نظری در زمینه ریاضیات دارید مطرح نمایید .در صورت امکان به آن می پردازم. من دوست دارم برای یافتن پاسخ به سوالات و حل پروژه های علمی با دیگران همکاری نمایم.در صورتی که شما هم بامن هم عقیده هستید با من تماس بگیرید.
در این وبلاگ به ریاضیات و کاربردهای آن و تحقیقات در آنها پرداخته می شود. مطالب در این وبلاگ ترجمه سطحی و اولیه است و کامل نیست.در صورتی سوال یا نظری در زمینه ریاضیات دارید مطرح نمایید .در صورت امکان به آن می پردازم. من دوست دارم برای یافتن پاسخ به سوالات و حل پروژه های علمی با دیگران همکاری نمایم.در صورتی که شما هم بامن هم عقیده هستید با من تماس بگیرید.