ادامه نقشه خطی

ماتریس ها [ ویرایش ]

اگر V و W هستند محدود بعدی فضاهای برداری و یک اساس برای هر فضای برداری تعریف شده است، پس از آن هر نقشه های خطی از V به W می تواند توسط یک نمایندگی ماتریس . [9] این مفید است زیرا محاسبات بتن را امکان پذیر می کند. ماتریس نمونه هایی از نقشه های خطی عملکرد: اگر واقعی است متر × N ماتریس، پس از آن F ( X ) = X توصیف خطی نقشه R N → R متر (نگاه کنید به فضای اقلیدسی ).

بگذارید { v 1 ،…، v n } مبنایی برای V باشد. سپس هر بردار v در V با ضرایب c 1 ،… ، c n در زمینه R به طور منحصر به فرد تعیین می شود :

${\ displaystyle c_ {1} \ mathbf {v} _ {1} + \ cdots + c_ {n} \ mathbf {v} _ {n}.}$

اگر f : V → W یک نقشه خطی است ،

${\ displaystyle f \ left (c_ {1} \ mathbf {v} _ {1} + \ cdots + c_ {n} \ mathbf {v} _ {n} \ right) = c_ {1} f \ چپ (\ mathbf {v} _ {1} \ right) + \ cdots + c_ {n} f \ left (\ mathbf {v} _ {n} \ right)،}$

که نشان می دهد تابع f کاملاً توسط بردارهای f ( v 1 ) ،… ، f ( v n ) تعیین می شود. حال بگذارید { w 1 ،…، w m } مبنایی برای W باشد. سپس می توانیم هر بردار f ( v j ) را به صورت زیر نشان دهیم

${\ displaystyle f \ left (\ mathbf {v} _ {j} \ right) = a_ {1j} \ mathbf {w} _ {1} + \ cdots + a_ {mj} \ mathbf {w} _ {m} .}$

بنابراین، تابع f را به طور کامل توسط مقادیر تعیین IJ . اگر ما این ارزش ها را به یک قرار متر × N ماتریس M ، پس ما به راحتی می توانید از آن استفاده کنید برای محاسبه خروجی بردار F برای هر بردار در V . برای به دست آوردن M ، هر ستون j از M یک بردار است

${\ displaystyle {\ start {pmatrix} a_ {1j} & \ cdots & a_ {mj} \ end {pmatrix}} ^ {\ textf {T}}}$

مربوط به f ( v j ) همانطور که در بالا تعریف شده است. برای تعریف واضح تر آن ، برای برخی از ستون های j که مربوط به نقشه برداری f ( v j ) است ،

${\ displaystyle \ mathbf {M} = {\ begin {pmatrix} \ \ cdots & a_ {1j} & \ cdots \ \\ & \ vdots & \\ & a_ {mj} & \ end {pmatrix}}}$

که در آن M ماتریس f است . به عبارت دیگر، هر ستون J = 1، ...، N است یک بردار متناظر F ( V J ) که مختصات 1 J ، ...، MJ عناصر ستون j ام . یک نقشه خطی ممکن است توسط بسیاری از ماتریس ها نشان داده شود. این بدان دلیل است که مقادیر عناصر یک ماتریس به مبانی انتخاب شده بستگی دارد.

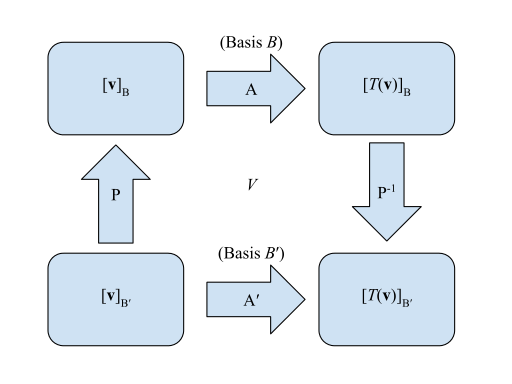
ماتریس های یک تحول خطی را می توان بصری نشان داد:

ماتریس برای ${\ textstyle T}$ نسبت به ${\ متن سبک B}$ : ${\ textstyle A}$
ماتریس برای ${\ textstyle T}$ نسبت به ${\ textstyle B '}$ : ${\ textstyle A '}$
ماتریس انتقال از ${\ textstyle B '}$ به ${\ متن سبک B}$ : ${\ متن سبک P}$
ماتریس انتقال از ${\ متن سبک B}$ به ${\ textstyle B '}$ : ${\ textstyle P ^ {- 1}}$

طوری که از گوشه پایین سمت چپ شروع می شود ${\ textstyle \ left [{\ vec {v}} \ right] _ {B '}}$ و به دنبال گوشه پایین سمت راست می گردیم ${\ textstyle \ چپ [T \ چپ ({\ vec {v}} \ راست) \ راست] _ {B '}}$ ، یکی چپ چپ می شود - یعنی ، ${\ textstyle A '\ left [{\ vec {v}} \ right] _ {B'} = \ left [T \ left ({\ vec {v}} \ right) \ right] _ {B '}}$ . روش معادل آن ، روش "طولانی تر" است که از همان نقطه در جهت عقربه های ساعت حرکت می کند به طوری که ${\ textstyle \ left [{\ vec {v}} \ right] _ {B '}}$ با چپ ضرب می شود ${\ textstyle P ^ {- 1} AP}$ ، یا ${\ textstyle P ^ {- 1} AP \ left [{\ vec {v}} \ right] _ {B '} = \ left [T \ left ({\ vec {v}} \ right) \ right] _ {B '}}$ .

نمونه هایی از ماتریس های تحول خطی [ ویرایش ]

در فضای دو بعدی نقشه های خطی R 2 توسط ماتریس های واقعی 2 × 2 توصیف می شوند . اینها چند نمونه است:

چرخش
- در خلاف جهت عقربه های ساعت با 90 درجه:
  ${\ displaystyle \ mathbf {A} = {\ start {pmatrix} 0 & -1 \\ 1 & 0 \ end {pmatrix}}}$
- با یک زاویه θ خلاف جهت عقربه های ساعت:
  ${\ displaystyle \ mathbf {A} = {\ start {pmatrix} \ cos \ theta & - \ sin \ theta \\\ sin \ theta & \ cos \ theta \ end {pmatrix}}}$
بازتاب
- در مورد محور x :
  ${\ displaystyle \ mathbf {A} = {\ start {pmatrix} 1 & 0 \\ 0 & -1 \ end {pmatrix}}}$
- در مورد محور y :
  ${\ displaystyle \ mathbf {A} = {\ start {pmatrix} -1 & 0 \\ 0 & 1 \ end {pmatrix}}}$
- در مورد محور با زاویه θ :
  ${\ displaystyle \ mathbf {A} = {\ start {pmatrix} {\ frac {1- \ tan ^ {2} \ theta} {\ tan ^ {2} \ theta +1}} و {\ frac {2 \ tan \ theta} {\ tan ^ {2} \ theta +1}} \\ {\ frac {2 \ tan \ theta} {\ tan ^ {2} \ theta +1}} & {\ frac {1- \ tan ^ {2} \ theta} {\ tan ^ {2} \ theta +1}} \ end {pmatrix}}}$
  - توجه داشته باشید که $\ برنزه \ تتا$ شیب خط عبوری از مبدا است
مقیاس گذاری توسط 2 در همه جهات:
${\ displaystyle \ mathbf {A} = {\ start {pmatrix} 2 & 0 \\ 0 & 2 \ end {pmatrix}} = 2 \ mathbf {I}}$
نقشه برشی افقی :
${\ displaystyle \ mathbf {A} = {\ start {pmatrix} 1 & m \\ 0 & 1 \ end {pmatrix}}}$
فشار نقشه برداری :
${\ displaystyle \ mathbf {A} = {\ start {pmatrix} k & 0 \\ 0 & {\ frac {1} {k}} \ end {pmatrix}}}$
طرح ریزی روی محور y :
${\ displaystyle \ mathbf {A} = {\ start {pmatrix} 0 & 0 \\ 0 & 1 \ end {pmatrix}}.}$

شکل گیری نقشه های خطی جدید از داده های داده شده [ ویرایش ]

ترکیب نقشه های خطی خطی است: اگر f : V → W و g : W → Z خطی هستند ، ترکیب آنها g ∘ f : V → Z نیز چنین است . آن را از این میشود که کلاس از همه فضاهای برداری بیش از یک میدان داده K ، همراه با K -Linear به عنوان نقشه morphisms ، اشکال دسته .

معکوس از یک نقشه خطی، که تعریف شده است، یک نقشه خطی.

اگر f 1 : V → W و f 2 : V → W خطی هستند ، پس جمع نقطه ای آنها f 1 + f 2 نیز (که توسط ( f 1 + f 2 تعریف می شود )) ( x ) = ( f 1 ( x ) + f 2 ( x )) .

اگر f : V → W خطی است و a عنصری از زمین زمین K است ، پس نقشه af که با ( af ) تعریف شده ( x ) = a ( f ( x )) نیز خطی است.

بنابراین مجموعه L ( V ، W ) نقشه های خطی از V به W خود یک فضای برداری بر روی K را تشکیل می دهد ، گاهی اوقات Hom ( V ، W ) را نشان می دهد . علاوه بر این ، در مورد V = W ، این فضای برداری (نشان داده شده پایان ( V ) ) یک جبر انجمنی تحت ترکیب نقشه ها است ، زیرا ترکیب دو نقشه خطی دوباره یک نقشه خطی است ، و ترکیب نقشه ها همیشه همراه است . در زیر این مورد با جزئیات بیشتری مورد بحث قرار گرفته است.

مجدداً به حالت بعدی محدود داده می شود ، اگر بازها انتخاب شده باشند ، ترکیب نقشه های خطی مربوط به ضرب ماتریس ، جمع نقشه های خطی مربوط به جمع ماتریس است و ضرب نقشه های خطی با مقیاس مربوط به ضرب ماتریس با مقیاس

+ نوشته شده در جمعه هجدهم مهر ۱۳۹۹ ساعت 11:54 توسط علی رضا نقش نیلچی |

ریاضیات

آموزش ریاضی