بخشی از یک سریال در
تجزیه و تحلیل رگرسیون
رگرسیون خطی.svg
مدل ها
برآورد کردن
زمینه

رگرسیون مقطعی ، همچنین به عنوان رگرسیون قطعه ای یا رگرسیون چوب شکسته شناخته می شود ، روشی در تجزیه و تحلیل رگرسیون است که در آن متغیر مستقل به فواصل تقسیم می شود و یک بخش خط جداگانه برای هر بازه متناسب است. تجزیه و تحلیل رگرسیون مقطعی همچنین می تواند با تقسیم متغیرهای مختلف مستقل بر روی داده های چند متغیره انجام شود. رگرسیون مقطعی زمانی مفید است که متغیرهای مستقل ، در گروه های مختلف جمع شده و روابط متفاوتی را بین متغیرهای این مناطق نشان دهند. مرزهای بین بخشها نقطه شکست هستند .

رگرسیون خطی تقسیم شده رگرسیون تقسیم شده است که به موجب آن روابط در فواصل با رگرسیون خطی بدست می آید .

 

فهرست

رگرسیون خطی تقسیم شده ، دو بخش [ ویرایش ]

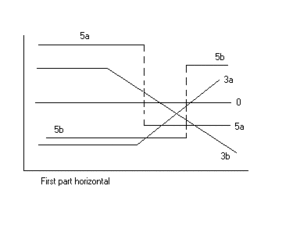
اندام 1 افقی

اندام اول شیب دار است

اندام اول شیب دار است

رگرسیون خطی تقسیم شده با دو بخش جدا شده توسط یک نقطه شکست می تواند برای تعیین کمیت تغییر ناگهانی عملکرد پاسخ (Yr) یک عامل تأثیرگذار متفاوت ( x ) مفید باشد. نقطه شکست می تواند به عنوان یک مقدار حیاتی ، ایمن یا آستانه تفسیر شود که فراتر یا زیر آن اثرات (غیر) مطلوبی رخ می دهد. نقطه شکست می تواند در تصمیم گیری مهم باشد [1]

این ارقام برخی از نتایج و انواع رگرسیون قابل دستیابی را نشان می دهد.

تجزیه و تحلیل رگرسیون قطعه قطعه شده است به حضور مجموعه ای از (بر اساس Y، X ) داده ها، که در آن Y است متغیر وابسته و ایکس متغیر مستقل .

روش حداقل مربعات به طور جداگانه برای هر بخش اعمال می شود ، که با استفاده از آن دو خط رگرسیون متناسب با مجموعه داده ها به همان اندازه که ممکن است در حالی که به حداقل رساندن مجموع مربعات اختلافات (SSD) بین مقادیر مشاهده شده ( y ) و محاسبه شده (Yr) از متغیر وابسته ، منجر به دو معادله زیر می شود:

  • سال = یک 1 . x + K 1     برای x 
  • سال = یک 2 . x + K 2     برای x > BP (نقطه شکست)

جایی که:

Yr مقدار مورد انتظار (پیش بینی شده) y برای مقدار مشخصی از x است .

A 1 و A 2 ضرایب رگرسیون هستند (نشان دهنده شیب بخشهای خط).

K 1 و K 2 ثابت های رگرسیون هستند (نشان دهنده رهگیری در محور- y ).

داده ها ممکن است انواع یا روندهای مختلفی را نشان دهند ، [2] ارقام را ببینید.

این روش همچنین دارای دو ضریب همبستگی (R) است:

  • R_ {1} ^ {2} = 1 - {\ frac {\ sum (y-Y_ {r}) ^ {2}} {\ sum (y-Y _ {{a1}}) ^ {2}}}     برای x 

و

  • R_ {2} ^ {2} = 1 - {\ frac {\ sum (y-Y_ {r}) ^ {2}} {\ sum (y-Y _ {{a2}}) ^ {2}}}     برای x > BP (نقطه شکست)

جایی که:

\ sum (y-Y_ {r}) ^ {2} حداقل SSD در هر بخش است

و

Y a1 و Y a2 مقادیر متوسط y در بخشهای مربوطه هستند.

در تعیین مناسب ترین روند ، آزمایشات آماری باید انجام شود تا اطمینان حاصل شود (قابل توجه).

هنگامی که هیچ نقطه شکست قابل توجهی قابل تشخیص نیست ، باید بدون بازگشت از نقطه بازگشت به یک رگرسیون سقوط کرد.

مثال [ ویرایش ]

رگرسیون خطی تقسیم شده ، نوع 3b

برای شکل آبی در سمت راست که رابطه بین عملکرد خردل (Yr = Ym ، t / ha) و شوری خاک ( x = Ss ، بیان شده به عنوان هدایت الکتریکی محلول خاک EC در dS / m) را نشان می دهد ، : [3]

BP = 4.93 ، A 1 = 0 ، K 1 = 1.74 ، A 2 = -0.129 ، K 2 = 2.38 ، R 1 2 = 0.0035 (ناچیز) ، R 2 2 = 0.395 (قابل توجه) و:

  • Ym = 1.74 تن در هکتار برای Ss <4.93 (نقطه شکست)
  • Ym = .0.129 Ss + 2.38 تن در هکتار برای Ss> 4.93 (نقطه شکست)

نشان می دهد که شوری خاک <4.93 dS / m امن است و شوری خاک> 4.93 dS / m باعث کاهش عملکرد @ 0.129 تن در هکتار در واحد افزایش شوری خاک می شود.

این شکل همچنین نشان دهنده فواصل اطمینان و عدم اطمینان به شرح زیر است.

رویه های آزمون [ ویرایش ]

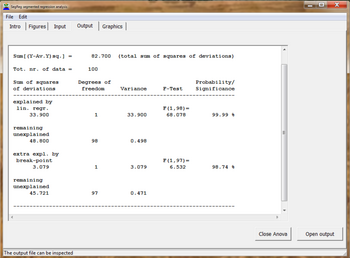
نمونه سری های زمانی ، نوع 5

نمونه ای از جدول ANOVA: در این حالت معرفی نقطه شکست بسیار قابل توجه است.

از آزمونهای آماری زیر برای تعیین نوع روند استفاده می شود:

  1. اهمیت نقطه انفصال (BP) با ابراز BP به عنوان تابعی از ضرایب رگرسیون 1 و A 2 و به معنای Y 1 و Y 2 از Y -Data و ابزار X 1 و X 2 از X داده (چپ و راست از BP) ، با استفاده از قوانین انتشار خطاها در جمع و ضرب برای محاسبه خطای استاندارد (SE) BP و استفاده از آزمون t دانشجو
  2. اهمیت A 1 و A 2 با استفاده از توزیع t دانش آموز و خطای استاندارد SE از A 1 و A 2
  3. اهمیت تفاوت A 1 و A 2 با استفاده از توزیع t دانشجو با استفاده از SE تفاوت آنها.
  4. اهمیت تفاوت Y 1 و Y 2 با استفاده از توزیع t دانشجو با استفاده از SE تفاوت آنها.
  5. یک روش آماری رسمی تر برای آزمایش وجود یک نقطه شکست ، از طریق آزمون نمره شبه است که نیازی به برآورد خط مقطعی ندارد [4] .

علاوه بر این ، از ضریب همبستگی همه داده ها (Ra) ، ضریب تعیین یا ضریب توضیح ، فواصل اطمینان عملکردهای رگرسیون و تحلیل ANOVA استفاده شده است . [5]

ضریب تعیین برای همه داده ها (Cd) ، که باید تحت شرایط تعیین شده توسط آزمون های اهمیت به حداکثر برسد ، از:

  • C_ {d} = 1 - {\ sum (y-Y_ {r}) ^ {2} \ over \ sum (y-Y_ {a}) ^ {2}}

جایی که Yr با توجه به معادلات رگرسیون سابق مقدار مورد انتظار (پیش بینی شده) y است و Ya میانگین همه مقادیر y است .

ضریب Cd بین 0 (بدون هیچ توضیحی) تا 1 (توضیح کامل ، تطابق کامل) است.
در یک رگرسیون خطی خالص ، بدون تقسیم ، مقادیر Cd و Ra 2 برابر هستند. در یک رگرسیون تقسیم شده ، Cd برای توجیه تقسیم بندی باید به طور قابل توجهی بزرگتر از Ra 2 باشد.

بهینه ارزش نقطه انفصال ممکن است به طوری که ضریب سی دی پیدا شده است حداکثر .

دامنه بدون اثر [ ویرایش ]

تصویر محدوده ای از X = 0 تا X = 7.1 که هیچ تاثیری روی آن وجود ندارد.

رگرسیون مقطعی اغلب برای تشخیص اینکه متغیر توضیحی (X) در متغیر وابسته (Y) هیچ تأثیری ندارد ، استفاده می شود ، در حالی که فراتر از دسترس ، یک پاسخ واضح ، مثبت یا منفی وجود دارد. دسترسی به هیچ تأثیری را نمی توان در قسمت اولیه دامنه X یا بالعکس در قسمت آخر آن یافت. برای تجزیه و تحلیل "بدون تأثیر" ، استفاده از روش حداقل مربعات برای تحلیل رگرسیون تقسیم شده [6]ممکن است مناسبترین تکنیک نباشد زیرا هدف این است که بیشترین کششی را پیدا کنیم که بتوان رابطه YX را دارای شیب صفر دانست در حالی که فراتر از شیب رسیدن به طور قابل توجهی با صفر متفاوت است اما دانش در مورد بهترین مقدار این شیب مادی نیست روش یافتن دامنه بدون اثر ، رگرسیون نسبی پیشرونده [7] در محدوده است و دامنه را با گام های کوچک گسترش می دهد تا زمانی که ضریب رگرسیون به طور قابل توجهی از صفر متفاوت شود.

در شکل بعدی نقطه شکست در X = 7.9 یافت می شود در حالی که برای همان داده ها (شکل آبی بالا را برای عملکرد خردل ببینید) ، روش حداقل مربعات نقطه شکست فقط در X = 4.9 است. مقدار دوم کمتر است ، اما تناسب داده ها فراتر از نقطه شکست بهتر است. از این رو ، این به روش تجزیه و تحلیل بستگی دارد که چه روشی باید استفاده شود.

همچنین به [ ویرایش ] مراجعه کنید

منبع

https://en.wikipedia.org/wiki/Segmented_regression