نوار موبیوس
اشعه ترسیم طرح پارامتری یک نوار موبیوس.
یک نوار Möbius با یک تکه کاغذ و نوار ساخته شده است. اگر طول آن توسط مورچه خزیده شود ، مورچه ها با گذر از هر دو طرف کاغذ ، بدون آنکه هیچ لبه ای را پشت سر بگذارند ، به نقطه شروع خود باز می گردند.
یک نوار Möbius بهم نمی خورد اما طرح آن در 2 بعد انجام می شود.
در ریاضیات ، یک نوار موبیوس ، باند ، و یا حلقه ( آمریکا : / متر oʊ ب من ə بازدید کنندگان ، متر eɪ - / وزارت بهداشت -bee-əs، MAY - ، بریتانیا : / متر ɜː ب من ə بازدید کنندگان / ؛ [ 1] آلمانی: [møːbi̯ʊs] )، همچنین املای موبیوس یا موبیوس ، یک است سطحتنها با یک طرف (هنگامی که در فضای سه بعدی اقلیدسی تعبیه شده است) و تنها یک منحنی مرزی . نوار Möbius ساده ترین سطح غیر جهت دار است. این می تواند به عنوان یک سطح حاکم تحقق یابد . کشف آن به طور مستقل به ریاضیدانان آلمانی یوهان بندیکت لیستینگ و آگوست فردیناند مبیوس در سال 1858 نسبت داده شده است ، [2] [3] [4] [5] گرچه ساختارهای مشابهی در موزائیک های رومی قابل مشاهده است. 200–250 م. [6] [7]
یک نمونه از نوار Möbius را می توان با گرفتن یک نوار کاغذ ، دادن یک انتهای نیم پیچ و سپس پیوستن به انتها برای تشکیل یک حلقه ایجاد کرد. مرز آن یک خم ساده بسته که می توان با تک ترسیم شده است unknotted رشته. هر نوع هومومورفيك فضايي توپولوژيك به اين مثال ، نوار Möbius نيز گفته مي شود كه امكان تنوع بسياري گسترده از تحقيقات هندسي را به عنوان سطحي با اندازه و شكل مشخص فراهم مي كند. به عنوان مثال ، هر مستطیل را می توان با برگرداندن جهت جهت ، به لبه سمت چپ به لبه راست چسبانید. برخی ، اما نه همه ، از این موارد می توان به عنوان سطحی در فضای اقلیدسی مدل سازی کرد . یک سطح کاملاً مرتبط ، اما نه هومومورفیک ، باند کاملاً باز Möbius است، یک سطح بدون مرز که در آن عرض نوار بی نهایت گسترش می یابد تا به یک خط اقلیدسی تبدیل شود.
نیم چرخش در جهت عقربه های ساعت به نوار موبیوس تعبیه شده است که نمی تواند حرکت کند یا کشیده شود و نیم پیچش را در جهت عقربه های ساعت به دست آورد. بنابراین ، یک نوار Möbius که در فضای اقلیدسی تعبیه شده است یک جسم کیرال با دست راست یا چپ است. نوار Möbius همچنین می تواند با پیچاندن نوار در هر زمان غیرعادی یا با گره زدن و پیچاندن نوار قبل از پیوستن به انتهای آن ، تعبیه شود.
یافتن معادلات جبری برش نوار Möbius ساده است ، اما این معادلات همان شکل هندسی را که مدل کاغذ پیچ خورده در بالا است توصیف نمی کنند. چنین مدل های کاغذی سطوح قابل توسعه ای هستند که دارای انحنای صفر گاوسی هستند و می توان با معادلات دیفرانسیل-جبری توصیف کرد . [8]
مشخصه اویلر از نوار موبیوس است صفر .
مدل تعاملی 3D از نوار Möbius
فهرست
خواص [ ویرایش ]
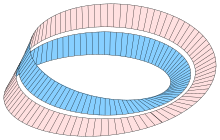
پس از قطع نوار Möbius: یک نوار غیر Möbius
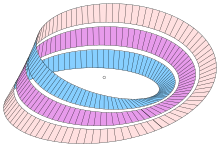
دو بار برش نوار Möbius: یک نوار Möbius (بنفش) ، یک نوار غیر Möbius
نوار Möbius دارای چندین ویژگی کنجکاو است. خطی که در امتداد لبه کشیده شده است در یک دایره کامل حرکت می کند تا نقطه مقابل نقطه شروع. در صورت ادامه ، خط به نقطه شروع برمی گردد و دو برابر طول نوار اصلی است: این منحنی مداوم منفرد در کل مرز عبور می کند.
برش یک نوار Möbius در امتداد خط وسط با یک جفت قیچی ، یک نوار طولانی با دو پیچش کامل در آن ، به جای دو نوار جداگانه ، باز می کند. نتیجه یک نوار Möbius نیست بلکه هومومورف به یک استوانه است. این اتفاق می افتد زیرا نوار اصلی فقط یک لبه دارد ، دو برابر طول نوار اصلی. برش یک لبه مستقل دوم با همان طول ایجاد می کند ، نیمی از هر طرف قیچی. قطع این نوار جدید و طولانی تر از وسط ، دو نوار به دور یکدیگر ایجاد می کند که هر کدام دارای دو پیچ و تاب کامل هستند.
اگر نوار در حدود یک سوم از لبه بریده شود ، دو نوار ایجاد می کند: مرکز سوم نوار باریک Möbius است ، به طول همان نوار اصلی. دیگر نوار نازک با دو پیچ و تاب کامل ، محله ای از لبه نوار اصلی است که دو برابر طول نوار اصلی دارد. [2]
نوارهای مشابه دیگر را می توان با پیوستن به طور مشابه نوارهایی با دو یا بیشتر نیم پیچ در آنها به جای یکی به دست آورد. به عنوان مثال ، نوار با سه پیچ و تاب نیمه ، هنگام تقسیم طول ، تبدیل به نوار پیچ خورده گره خورده در گره سه پایه ای می شود . (اگر این گره جدا شود ، نوار دارای هشت پیچ و تاب نیمه نیم است.) یک نوار با پیچ و تاب N N ، در صورت جدا شدن ، تبدیل به نوار با پیچ و تاب های کامل N + 1 می شود. [2] پیچاندن اضافی و اتصال مجدد انتهای آن ، چهره هایی به نام حلقه های پارادرومیک ایجاد می کند .
منبع
در این وبلاگ به ریاضیات و کاربردهای آن و تحقیقات در آنها پرداخته می شود. مطالب در این وبلاگ ترجمه سطحی و اولیه است و کامل نیست.در صورتی سوال یا نظری در زمینه ریاضیات دارید مطرح نمایید .در صورت امکان به آن می پردازم. من دوست دارم برای یافتن پاسخ به سوالات و حل پروژه های علمی با دیگران همکاری نمایم.در صورتی که شما هم بامن هم عقیده هستید با من تماس بگیرید.