ادامه فرم های دیفرانسیل

$\ fill {تراز} \ mathrm d (a_1 \ cdot \ mathrm dx_1 + a_2 \ cdot \ mathrm dx_2) & = \ mathrm da_1 \ wedge \ mathrm dx_1 + \ mathrm da_2 \ wedge \ mathrm dx_2 \ \ [=] سمت چپ (\ frac {\ جزئی a_1} {\ جزئی x_1} \ mathrm dx_1 + \ frac {\ partial a_1} {\ partial x_2 m \ mathrm dx_2 \ right) \ wedge \ mathrm dx_1 + + left (\ frac {\ partial a_2} {\ جزئی x_1} \ mathrm dx_1 + \ frac {\ جزئی a_2} {\ جزئی x_2} \ mathrm dx_2 \ درست) \ گوه \ mathrm dx_2 \\ [0.5em] & = frac {\ جزئی a_1} { \ partial x_1} \ cdot \ mathrm dx_1 \ wedge \ mathrm dx_1 + \ frac {\ partial a_1} {\ partial x_2} \ cdot \ mathrm dx_2 \ wedge \ mathrm dx_1 + \ frac {\ partial a_2} part part قسمت \ cdot \ mathrm dx_1 \ wedge \ mathrm dx_2 + \ frac {\ partial a_2} {\ part_ x_2} \ cdot \ mathrm dx_2 \ wedge \ mathrm dx_2 \\ [0.5em] & = سمت چپ (\ frac {\ partial a_ {\ جزئی x_1} - \ frac {\ جزئی a_1 _1 {\ جزئی x_2} \ درست) \ cdot \ mathrm dx_1 \ wedge \ mathrm dx_2. \ end {تراز}$

به طور کلی ، مشتقات بیرونی یک فرم اعمال می شود

برای $n = 3$ بنابراین ضرایب مشتقات بیرونی یک فرم چرخش بردار تشکیل شده از ضرایب 1 فرم را تشکیل می دهد.

عملیات بیشتر روی فرم های دیفرانسیل [ ویرایش | ویرایش منبع ]

محصول داخلی [ ویرایش | ویرایش منبع ]

بودن $X \ در T (M)$ یک میدان بردار صاف محصول داخلی یک نقشه خطی است

$i_X \ colon \ Omega ^ k (M) \ to \ Omega ^ {k-1} (M)،$

توسط

$\ omega \ mapsto \ امگا (X ، \ cdot ، \ ldots ، \ cdot)$

داده شده است یعنی محصول درونی یکی را تشکیل می دهد $ک$ -شکل $\ امگا$ روی $(k-1)$ با وصل کردن شکل به یک فیلد بردار ثابت ، از آنجا دور شوید {\ نمایشگر X} $ایکس$ ارزیابی می شود این نقشه برداری یک آنالوگ از تانسور taper در فضای اشکال دیفرانسیل است. به همین دلیل است که این عمل گاهی به انگلیسی گفته می شود انقباض.

محصول داخلی $i_X$ یک IS ضد اشتقاق . یعنی ، برای $\ امگا \ در \ امگا ک (م)$ و $\ nu \ in \ Omega ^ l (M)$ قانون لایب نیتس اعمال می شود

$i_X (\ omega \ wedge \ nu) = (i_X \ omega) \ گوه \ nu + (-1) ^ k \ omega \ گوه (i_X \ nu).$

در مورد محصول داخلی نیز صدق می کند. $i_X \ circ i_X = 0.$

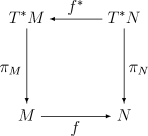
حمل و نقل برگشتی (بازپرداخت) اشکال دیفرانسیل [ ویرایش | ویرایش منبع ]

→ نوشتار اصلی : حمل و نقل بازگشت

طرح عقب نشینی ، $T ^ {*} م$ بسته كانتژنت منیفولد است $م$ و بر این اساس برای $ن$

است $f \ colon M \ to N$ نقشه برداری صاف بین مشتقپذیر منیفولدهای است $\ امگا \ در \ امگا ک (ن)$ ابزار $f$ فرم بازیابی شده $(f ^ * \ امگا) \ در \ امگا ک (م)$ به شرح زیر تعریف شده است:

$(f ^ * \ omega) (X_1 ، \ ldots ، X_k): = \ omega (\ mathrm df (X_1)، \ ldots، \ mathrm df (X_k)) \،.$

این است $df \ colon TM \ to TN$ توسط $f$ نقشه برداری از سرب ، همچنین "فشار رو به جلو" نامیده می شود. برداشت با سازنده خارجی و محصول خارجی سازگار است:

$f ^ * (\ mathrm d \ omega) = \ mathrm d (f ^ * \ امگا)$

(با جزئیات بیشتر نوشته شده است: در سمت چپ $\ mathrm d = \ mathrm d ^ {(N)$ ، در سمت راست در برابر آن $\ mathrm d = \ mathrm d ^ {(M)$ ) و

$f ^ * (\ omega \ wedge \ eta) = (f ^ * \ omega) \ گوه (f ^ * \ eta)$

برای همه $\ omega ، \ eta \ in \ Omega ^ {pback} (N)$

به طور خاص ناشی از $f$ نقشه بین گروه های کوهشناسی شناسی د رام (به تصویر زیر مراجعه کنید)

$f ^ {pback} \ colon \ mathrm H ^ k _ {\ mathrm {dR}} (N) \ longrightarrow \ mathrm H ^ k _ {\ mathrm {dR}} (M)،$

مخالف جهت فلش $f \ colon M \ to N$ باید رعایت شود ("عقب نشینی" ، "زندگی مشترک" به جای "همسانی").

فرم دوگانه و اپراتور ستاره [ ویرایش | ویرایش منبع ]

→ نوشتار اصلی : اپراتور ستاره هاج

اشکال خارجی در یک در نظر گرفته می شود $ن$ فضای بصری که در آن یک محصول داخلی (متریک) تعریف می شود به گونه ای که مبنای متعامد باشد $تخم مرغ}$ از اتاق می تواند تشکیل شود. که تا حد بیرونی درجه $ک$ در این $ن$ -فضای بعدی یک شکل دوتایی است $(نک)$ -شکل

$* (e_1 \ wedge e_2 \ wedge \ ldots \ wedge e_k) = e_ {k + 1 \ wedge e_ {k + 2 \ wedge \ ldots \ wedge e_n.$

هر دو طرف به شکلی گرا نوشته شده اند. به طور رسمی ، فرم دوگانه با استفاده از (هاج) به دست می آید $*$ اپراتور. به خصوص در مورد اشکال دیفرانسیل در فضای سه بعدی اقلیدسی نتایج زیر:

$* \ mathrm {d} x = \ mathrm {d} y \ wedge \ mathrm {d} z$

$* \ mathrm {d} y = \ mathrm {d} z \ wedge \ mathrm {d} x$

$* \ mathrm {d} z = \ mathrm {d} x \ wedge \ mathrm {d} y$

با 1 فرم $dx ، dy ، dz$ . در نظر گرفته شده است که نظم گرا در اینجا ${\ نمایشگر (y ، z) ، (x ، y)$ و ${\ نمایشگر (z، x)$ است (تبادل چرخه ای در $(x ، y ، z)$ )

$*$ -Symbol قصد دارد تا این واقعیت را تأکید کند که یک محصول داخلی در فضای اشکال در فضای زیرین وجود دارد $م$ داده می شود زیرا $\ آلفا \ گوه * \ بتا$ می تواند برای دو نفر باشد $ک$ -شکل دادن $\ آلفا$ و $\ بتا$ به عنوان فرم حجم و انتگرال بنویسید

$(\ alpha، \ beta) = \ int_M \ alpha \ wedge * \ beta$

یک عدد واقعی را برمی گرداند علاوه بر این دوگانه نشان می دهد که برنامه دوگانه به یک $ک$ دوباره فرار کن $ک$ نتایج نتایج: به جز علامت ، که باید جداگانه در نظر گرفته شود. دقیق تر مربوط به یکی $ک$ فرم در یک $ن$ فضای بعدی که معیار آن امضا است $s$ دارای $\ displaystyle s = + 1$ در فضای اقلیدسی ، $s = -1$ در اتاق مینکوفسکی):

$** \ alpha = (- 1) ^ {k (nk)} s \؛ \ alpha$

در بالا نشان داده شد که چگونه در فضای اقلیدسی 3 بعدی با مشتق خارجی از یک شکل $\ آلفا$ فرم $د \ گوه \ آلفا$ نتایج تجزیه و تحلیل بردار با مؤلفه های بردار چرخش به عنوان ضرایب. شما می توانید استفاده کنید $*$ -Operators هم اکنون نیز بطور رسمی به صورت 1 فرم ( بردار قرمز ) می نویسند : $* (d \ wge \ alpha)$ . $*$ -عكس كننده براي ترجمه "قضيه استوكس" كه در بالا فرمول آناليز بردار است ، استفاده مي شود.

منبع

https://de.wikipedia.org/wiki/Differentialform

+ نوشته شده در شنبه یکم شهریور ۱۳۹۹ ساعت 0:25 توسط علی رضا نقش نیلچی |

ریاضیات

آموزش ریاضی