حلقه گروهی

در جبر ، یک حلقه گروهی یک ماژول رایگان و در عین حال یک حلقه است که به روش طبیعی از هر حلقه معین و هر گروه مشخص ساخته می شود . به عنوان یک ماژول رایگان ، حلقه مقیاس آن حلقه داده شده است و اساس آن با گروه معین یک به یک است. به عنوان حلقه ، قانون اضافه شدن آن از ماژول رایگان است و ضرب آن براساس قانون گروه "داده شده" است. كمتر رسمي ، يك حلقه گروهي تعميم يك گروه خاص است ، با اتصال هر عنصر گروه "يك عامل وزني" از حلقه معين.

یک حلقه گروهی به عنوان یک جبر گروهی نیز گفته می شود ، زیرا در واقع یک جبر بیش از حلقه معین است. جبر گروهی بر روی یک زمینه ساختار دیگری از جبر هاپف دارد . در این حالت ، به این ترتیب یک گروه جبر هاپف گروهی نامیده می شود .

دستگاه حلقه های گروه به ویژه در تئوری نمایش گروهها مفید است .

فهرست

تعریف [ ویرایش ]

بگذارید G یک گروه باشد ، به صورت چندگانگی نوشته شود و بگذارید R یک حلقه باشد. حلقه گروه از G بیش از R ، که ما توسط دلالت R [ G ] (و یا به سادگی RG )، مجموعه ای از نگاشت است ج : G → R از پشتیبانی محدود ، [1] که در آن ماژول محصول اسکالر αf از یک اسکالر α در R و یک بردار (یا نقشه برداری) f به عنوان بردار تعریف می شود $x \ mapsto \ alpha \ cdot f (x)$ ، و جمع گروه ماژول دو بردار f و g به عنوان بردار تعریف می شود $x \ mapsto f (x) + g (x)$ . برای تبدیل گروه افزودنی R [ G ] به حلقه ، محصول f و g را بردار تعریف می کنیم

$x \ mapsto \ sum_ {uv = x} f (u) g (v) = \ sum_ {u \ in G} f (u) g (u ^ {- 1} x).$

جمع بندی مشروع است زیرا f و g پشتیبانی محدود دارند و بدیهیات حلقه به آسانی تأیید می شوند.

برخی از تغییرات در نماد و اصطلاحات در حال استفاده هستند. به ویژه ، نگاشتهایی مانند f : G → R گاهی اوقات به عنوان آنچه "ترکیب رسمی خطی عناصر G ، با ضرایب در R " خوانده می شود ، نوشته شده است: [2]

$\ sum_ {g \ در G} f (g) گرم ،$

یا به سادگی

$\ sum_ {g \ در G} f_g گرم ،$

جایی که این باعث سردرگمی نمی شود. [1]

مثالها [ ویرایش ]

1. بگذارید G = C 3 ، گروه چرخه ای ترتیب 3 ، با ژنراتور $آ$ و عنصر هویت 1 G . یک عنصر r از C [ G ] را می توان به صورت نوشت

$r = z_0 1_G + z_1 a + z_2 a ^ 2 \،$

جایی که z 0 ، z 1 و z 2 در C قرار دارند ، اعداد پیچیده هستند . این همان چیزی است که یک حلقه چند جمله ای در متغیر است $آ$ به طوری که $\ displaystyle a ^ {3} = a ^ {0} = 1$ یعنی C [ G ] نسبت به حلقه C isomorphic است [ $آ$ ] ${\ displaystyle (a ^ {3} -1)}$ . نوشتن یک عنصر مختلف بازدید کنندگان به عنوان

$s = w_0 1_G + w_1 a + w_2 a ^ 2 \،$

جمع آنها است

$r + s = (z_0 + w_0) 1_G + (z_1 + w_1) a + (z_2 + w_2) a ^ 2 \،$

و محصول آنها است

$rs = (z_0w_0 + z_1w_2 + z_2w_1) 1_G + (z_0w_1 + z_1w_0 + z_2w_2) a + (z_0w_2 + z_2w_0 + z_1w_1) a ^ 2.$

توجه کنید که عنصر هویت 1 G از G باعث تعبیه غیرقانونی حلقه ضریب (در این حالت C ) به C [ G ] می شود. با این حال صرفا صحبت کردن عنصر هویت ضربی C [ G ] 1⋅1 است G که در آن اولین 1 از C و دوم از G . عنصر هویت افزودنی صفر است.

هنگامی که G یک گروه غیرتجاری است ، باید هنگام ضرب اصطلاحات مراقب باشید ترتیب عناصر گروه (و نه بطور تصادفی رفت و آمد آنها) حفظ شود.

2. یک نمونه متفاوت از چند جمله های Laurent بر روی حلقه R است : اینها چیزی بیشتر یا کمتر از حلقه گروه گروه نامتناهی چرخه ای Z روی R نیست .

3. بگذارید Q یک گروه چهارگانه با عناصر باشد ${\ displaystyle \ {e، {\ bar {e} i، i، {\ bar {i} j، j، {\ bar {j}}، k، {\ bar {k}} \}}$ . حلقه گروه در نظر بگیرید R Q ، که در آن R مجموعه ای از اعداد حقیقی است. یک عنصر دلخواه از این حلقه گروه از نوع است

$\ displaystyle x_ {1} \ cdot e + x_ {2} \ cdot {\ bar {e}} + x_ {3} \ cdot i + x_ {4 \ cdot {\ bar {i} x + x_ {5 \ cdot j + x_ {6} \ cdot {\ bar {j}} + x_ {7} \ cdot k + x_ {8} \ cdot {\ bar {k}}}$

جایی که $x_ {من$ یک شماره واقعی است

ضرب ، مانند هر حلقه گروهی دیگر ، بر اساس عملکرد گروه تعریف می شود. مثلا،

$\ displaystyle {\ شروع {تراز شده} {\ big (} 3 \ cdot e + {\ sqrt {2}} \ cdot i big \ بزرگ) {\ big (} {\ frac {1} {2}} \ cdot {\ bar {j}} {\ big)} & = (3 \ cdot e) ({\ frac {1} {2}} \ cdot {\ bar {j}}) + ({\ sqrt {2}}) \ cdot i) ({\ frac {1} {2}} \ cdot {\ bar {j}}) \\ & = {\ frac {3} {2}} \ cdot {\ big (} (e) ( {\ bar {j}}) {\ big)} + {\ frac {\ sqrt {2}} {2}} \ cdot {\ big () (i) ({\ bar {j}}) {\ big )} \\ & = {\ frac {3} {2}} \ cdot {\ bar {j}} + {\ frac {\ sqrt {2}} {2}} \ cdot k \ end {تراز شده}. }$

توجه داشته باشید که R Q برابر با کواترنم های همیلتون بالای R نیست . این امر به این دلیل است که کواترنم های همیلتون روابط دیگری را در حلقه از قبیل $\ displaystyle -1 \ cdot i = -i$ ، در حالی که در گروه حلقه R Q ، $\ displaystyle -1 \ cdot i$ برابر نیست $\ displaystyle 1 \ cdot {\ bar {i}}}$ . برای خاص تر بودن ، R Q دارای ابعاد 8 به عنوان یک فضای بردار واقعی است ، در حالی که کواترنون های همیلتون دارای ابعاد 4 به عنوان یک فضای بردار واقعی هستند .

برخی از خصوصیات اساسی [ ویرایش ]

با فرض اینکه حلقه R یک عنصر واحد 1 دارد و واحد گروه را 1 G نشان می دهد ، حلقه R [ G ] حاوی یک ایزومورف subring به R است ، و گروه عناصر برگشت پذیر آن حاوی یک زیر گروه هم همسان با G است . برای در نظر گرفتن عملکرد شاخص 1 G } ، که وکتور f تعریف شده توسط آن است

$f (g) = 1 \ cdot 1_G + \ sum_ {g \ not = 1_G 0 \ cdot g = \ mathbf {1} _ {\ {1_G \}} (g) = \ شروع {موارد} 1 & g = 1_G \\ 0 & g \ ne 1_G \ end {موارد} ،$

مجموعه همه ضربهای مقیاس f از فرونشست ایزومورف R [ G ] به R است . و اگر ما بر روی نقشه هر عنصر بازدید کنندگان از G به تابع شاخص { بازدید کنندگان } است که بردار F تعریف

$f (g) = 1 \ cdot s + \ sum_ {g \ not = s} 0 \ cdot g = \ mathbf {1} _ {\ {s \}} (g) = \ fill {موارد} 1 & g = s \\ 0 & g \ ne s \ end {موارد}$

نقشه برداری حاصل یک همگنورفیسم گروه تزریقی است (با توجه به ضرب و نه علاوه بر این ، در R [ G ]).

اگر R و G هر دو متغیر باشند (یعنی ، R تبادل کننده است و G یک گروه abelian است ) ، R [ G ] متغیر است.

اگر H است زیر گروه از G ، سپس R [ H ] است subring از R [ G ]. به همین ترتیب ، اگر S یک غوطه وری از R باشد ، S [ G ] یک Subring از R [ G ] است.

اگر ترتیب گروه G به شدت بیشتر از 1 باشد؛ | G |> 1 ، سپس R [ G ] همیشه دارای تقسیم صفر است . برای مثال، یک عنصر گرم از G از سفارش | g |> 1. سپس 1 - g یک تقسیم کننده صفر است. بگذارید | g | = m > 1.

$\ displaystyle (1-g) (1 + g + ... + g ^ {m-1}) = 1-g ^ {m} = 1-1 = 0}$

به عنوان مثال ، حلقه گروه Z [ S 3 ] و عنصر ترتیب 3 g = (123) را در نظر بگیرید. در این مورد،

$\ displaystyle (1- (123)) (1+ (123) + (132)) = 1- (123) ^ {3} = 1-1 = 0}$

جبر گروهی بیش از یک گروه محدود [ ویرایش ]

جبری گروه به طور طبیعی در نظریه رخ نمایندگی گروه از گروه های محدود . جبر گروه K [ G ] در بالای یک میدان K در واقع حلقه گروه است که میدان K جای آن را گرفته است. به عنوان یک فضای مجموعه و بردار ، فضای بردار آزاد در G بر روی قسمت K است . یعنی برای x در K [ G ] ،

$x = \ sum_ {g \ in G} a_g g.$

جبر ساختار در فضای برداری با استفاده از ضرب در گروه تعریف شده است:

$g \ cdot h = Gh ،$

جایی که در سمت چپ ، g و h عناصر جبر گروه را نشان می دهند ، در حالی که ضرب در سمت راست عملیات گروه (مشخص شده توسط مخلوط کردن) است.

از آنجا که ضرب بالا می تواند گیج کننده، همچنین می توانید نوشتن بردارهای پایه از K [ G ] به عنوان E گرم (به جای گرم )، که در این صورت ضرب به عنوان نوشته شده است:

$e_g \ cdot e_h = e_ {Gh.$

تفسیر به عنوان توابع [ ویرایش ]

با اندیشیدن به فضای برداری رایگان به عنوان K توابع در -valued G ، ضرب جبر است پیچیدگی از توابع.

در حالی که جبر گروهی یک گروه محدود با فضای توابع موجود در گروه قابل شناسایی است ، اما برای یک گروه نامحدود اینها متفاوت هستند. جبر گروه ، متشکل از مبالغ محدود ، به توابع گروه مربوط است که به طور هم زمان بسیاری از نقاط را از بین می برد . از نظر توپولوژیکی (با استفاده از توپولوژی گسسته ) ، این عملکردها با پشتیبانی کم حجم مطابقت دارد .

با این حال ، جبر گروه K [ G ] و فضای توابع K G : = Hom ( G ، K ) دوگانه هستند: با توجه به یک عنصر از جبر گروه

$x = \ sum_ {g \ in G} a_g g$

و یک تابع در گروه f : G → K این جفت ها را به یک عنصر K از طریق

$(x ، f) = \ sum_ {g \ in G} a_g f (g) ،$

که مبلغ کاملاً مشخصی است زیرا متناهی است.

نمایندگی منظم [ ویرایش ]

مقاله اصلی: نمایندگی منظم

جبر گروهی یک جبر بیش از خود است. تحت مکاتبات بازنمایی بیش از ماژول های R و R [ G ] ، این نمایندگی منظم از گروه است.

به عنوان نمایندگی نوشته شده است ، این نمایندگی g ↦ ρ g با عملکردی است که توسط انجام شده است $\ rho (g) \ cdot e_h = e_ {Gh$ ، یا

$\ rho (g) \ cdot r = \ sum_ {h \ in G} k_h \ rho (g) \ cdot e_h = \ sum_ {h \ in G} k_h e_ {Gh}.$

خواص [ ویرایش ]

ابعاد فضای بردار K [ G ] دقیقا برابر با تعداد عناصر گروه است. زمینه K معمولاً به عنوان شماره های پیچیده C یا واقعیت R در نظر گرفته می شود ، به طوری که فرد در مورد جبرهای گروه C [ G ] یا R [ G ] بحث می کند.

جبر گروه C [ G ] از یک گروه محدود بیش از اعداد پیچیده ، یک حلقه نیمه نهایی است . این نتیجه ، قضیه Maschke ، به ما اجازه می دهد C [ G ] را به عنوان یک محصول محدود از حلقه های ماتریس با ورودی در C درک کنیم .

نمایندگی های یک جبر گروهی [ ویرایش ]

با توجه به اینکه K [ G ] یک جبر انتزاعی است ، ممکن است یک نماینده بتنی از جبر را بر روی یک فضای بردار V بخواهید . چنین نمایندگی

$\ tilde {\ rho}: K [G] \ Rightarrow \ mbox {End} (V).$

هومومورفيسم جبري از جبر گروه به مجموعه اندومورفيسم در V است . با توجه به اینکه گروه V با استفاده از بردار علاوه بر گروه داده می شود ، V در واقع یک K [ G ] -Module سمت چپ بالای گروه abelian V است . این در زیر نشان داده شده است ، که در آن هر محور یک ماژول تأیید می شود.

انتخاب R ∈ K [ G ] به طوری که

$\ tilde \ rho r (r) \ in \ mbox {End} (V).$

سپس $\ tilde \ rho r (r)$ در آن یک همجنسگرایی گروههای abelian است

$\ tilde {\ rho r (r) \ cdot (v_1 + v_2) = \ tilde {\ rho (r) \ cdot v_1 + \ tilde {\ rho (r) \ cdot v_2$

برای هر V 1 ، V 2 ∈ V . در مرحله بعد ، یکی متذکر می شود که مجموعه ی endomorphism های یک گروه abelian ، یک حلقه endomorphism است . نمایندگی $\ tilde \ rho$ هومومورفیسم حلقه ای است ،

$\ tilde {\ rho} (r + s) \ cdot v = \ tilde {\ rho} (r) \ cdot v + \ tilde {\ rho (s) \ cdot v$

برای هر دو R ، ها ∈ K [ G ] و V ∈ V . به همین ترتیب ، تحت ضرب ،

$\ tilde {\ rho (rs) \ cdot v = \ tilde {\ rho} (r) \ cdot \ tilde {\ rho (s) \ cdot v.$

سرانجام ، شخص این را دارد که این واحد به هویت نقشه برداری می شود:

$\ tilde {\ rho (1) \ cdot v = v$

که 1 واحد ضرب K [ G ] است. به این معنا که،

$1 = e_e$

بردار مطابق با عنصر هویت e در G است .

سه معادله آخر نشان می دهد که $\ tilde \ rho$ یک همگنورفیسم حلقه از K [ G ] گرفته شده به عنوان یک حلقه گروهی ، به حلقه endomorphism است. هویت اول نشان داد که عناصر فردی همگنورفیسم گروهی هستند. بنابراین ، یک نمایندگی $\ tilde \ rho$ سمت چپ است K [ G ] -module بر گروه آبلی V .

توجه داشته باشید که با توجه به یک فرمول کلی K [ G ] ، یک ساختار بردار-فضا بر روی V القا می شود ، در این صورت یک بدیهیات اضافی وجود دارد.

$\ tilde {\ rho} (ar) \ cdot v_1 + \ tilde {\ rho} (br) \ cdot v_2 = a \ tilde \ rho} (r) \ cdot v_1 + b \ tilde {\ rho} (r) \ cdot v_2 = \ tilde {\ rho} (r) \ cdot (av_1 + bv_2)$

برای اسکالر ، ب ∈ K .

هر نمایندگی گروهی

$\ rho: G \ rightarrow \ mbox {Aut} (V) ،$

با V یک فضای بردار بر روی زمینه K ، می توان به یک بازنمایی جبر گسترش داد

$\ tilde {\ rho}: K [G] \ Rightarrow \ mbox {End} (V) ،$

به سادگی با اجازه دادن $\ tilde {\ rho} (e_g) = \ rho (g)$ و بصورت خطی گسترش می یابد. بنابراین ، بازنمودهای گروه دقیقاً با بازنمودهای جبر مطابقت دارند و بنابراین ، به یک معنا خاص ، صحبت کردن در مورد یکی همان حرف زدن در مورد دیگری است.

مرکز جبر گروهی [ ویرایش ]

مرکز جبر گروه مجموعه ای از عناصر که با تمام عناصر از جبر گروه رفت و آمد است:

$\ displaystyle \ mathrm {Z} (K [G]): = \ left \ {z \ in K [G]: \ forall r \ in K [G] ، zr = rz \ Right \.}$

مرکز برابر با مجموعه ای از توابع کلاس است ، یعنی مجموعه عناصر ثابت در هر کلاس مزخرف

$\ displaystyle \ mathrm {Z} (K [G]) = \ left \ {\ sum _ {g \ in G} a_ {g} g: \ forall g، h \ in G، a_ {g} = a_ h ^ {- 1} Gh} \ درست \}.$

اگر K = C باشد ، مجموعه ای از شخصیت های غیر قابل برگشت از G ، یک پایه متعامد از Z ( K [ G ]) را با توجه به محصول داخلی تشکیل می دهد.

$\ left \ langle \ sum_ {g \ in G} a_g g، \ sum_ {g \ in G} b_g g \ Right \ rangle = \ frac {1} {| G |} \ sum_ {g \ in G} \ bar {a _g b_g.$

زنگ گروه بیش از یک گروه نامحدود [ ویرایش ]

در مورد G که بسیار بی حد یا غیرقابل شمارش است بسیار کمتر شناخته شده است و این یک منطقه از تحقیقات فعال است. [3] موردی که R زمینه زمینه اعداد پیچیده است احتمالاً موردی است که به بهترین وجه مورد بررسی قرار گرفته است. در این حالت ، ایروینگ کپلانسکی ثابت کرد که اگر a و b عناصر C [ G ] با ab = 1 هستند ، پس ba = 1 است . آیا R صحیح است اگر R زمینه ای از خصوصیات مثبت باشد ، ناشناخته است.

حدس بلند مدت کاپلانسکی (1940 پوند) می گوید اگر G یک گروه بدون پیچ خوردگی باشد و K یک زمینه است ، پس گروه حلقه K [ G ] هیچ تقسیم کننده صفر غیر بدیهی ندارد . این حدس معادل K [ G ] است که هیچ گونه نیلوکپی غیرمشخصی تحت همین فرضیه برای K و G ندارد .

در حقیقت ، شرط اینکه K یک میدان باشد ، می تواند به هر حلقه ای که می تواند در یک دامنه انتگرال تعبیه شود ، آرام شود .

حدس در کلیت عمومی باز است ، با این حال برخی موارد خاص از گروه های بدون چرخش نشان داده شده است که حدس و گمان صفر تقسیم کننده را برآورده می کنند. این شامل:

گروه های محصولات منحصر به فرد (به عنوان مثال گروه های قابل سفارش ، به ویژه گروه های رایگان )
گروه های قابل قبول ابتدایی (به عنوان مثال گروه های تقریبا بیلی )
گروه های پراکندگی - بخصوص گروههایی که آزادانه به طور همزمانی در درختان R عمل می کنند ، و گروههای اساسی گروههای سطح به جز گروههای اساسی مبالغ مستقیم یک ، دو یا سه نسخه از صفحه پروژکتی.

مورد G بودن یک گروه توپولوژیکی با جزئیات بیشتر در جبر گروه مقاله از یک گروه کاملاً فشرده بحث شده است .

نمایندگی های یک حلقه گروهی [ ویرایش ]

یک ماژول M بر روی R [ G ] سپس همانند یک نمایش خطی از G بر روی قسمت R است . هیچ دلیل خاصی برای محدود کردن R در اینجا زمینه وجود ندارد. با این حال ، نتایج کلاسیک ابتدا بدست آمد که R میدان پیچیده شماره و G یک گروه محدود باشد ، بنابراین این مورد سزاوار توجه جدی است. نشان داده شده است كه R [ G ] يك حلقه نيمه شبكه است ، در آن شرايط ، با پيامدهاي عميق براي بازنمايي گروه هاي محدود. به طور کلی ، هر زمان که ویژگیدر قسمت R ، ترتیب گروه محدود G تقسیم نمی شود ، سپس R [ G ] نیم قطعه است ( قضیه Maschke ).

هنگامی که G یک گروه محدود abelian است ، حلقه گروه قابل تغییر است و ساختار آن از نظر ریشه وحدت آسان است . هنگامی که R زمینه ای از خصوصیات p است ، و شماره اصلی p ترتیب ترتیب محدود G را تقسیم می کند ، سپس حلقه گروه نیمه نهایی نیست : دارای یک رادیکال غیر صفر از Jacobson است ، و این موضوع مربوط به نظریه نمایش مدولار است. شخصیت عمیق تر و خاص خود را دارد

نظریه طبقه بندی [ ویرایش ]

تنظیم [ ویرایش ]

از نظر قاطع ، ساخت حلقه گروه در مجاورت " گروه واحدها " قرار دارد. سرگرمی های زیر یک جفت فرعی هستند :

$\ displaystyle R [-] \ Colon \ mathbf {Grp} \ to R \ mathbf {{\ text -}} Alg}$

$\ displaystyle (-) ^ {\ بار} \ کولون R \ mathbf {{\ متن {-}} آلگ} \ به \ mathbf {Grp}}$

جایی که $display \ displaystyle R [-]$ یک گروه را به حلقه گروه خود بر روی R می برد ، و ${\ displaystyle (-) ^ {\ بار}}$ یک R -algebra را به گروه واحد خود می برد.

وقتی R = Z ، این یک رابطه بین دسته گروه ها و دسته حلقه ها ایجاد می کند ، و واحد پیوست گروه G را به گروهی می برد که شامل واحدهای بی اهمیت است: G × {± 1} = {± g . بطور کلی حلقه های گروهی شامل واحدهای غیرمستقیم هستند. اگر G دارای عناصر a و b باشد به گونه ای که $a ^ n = 1$ و ب عادی نمی شود

$\ langle \ rangle$ سپس مربع

$x = (a-1) b \ left (1 + a + a ^ 2 + ... + a ^ {n-1} \ Right)$

از این رو صفر است $(1 + x) (1-x) = 1$ . عنصر 1 + x واحدی از نظم نامتناهی است.

دارایی جهانی [ ویرایش ]

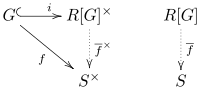
ضمیمه فوق ویژگی جهانی حلقه های گروه را بیان می کند. [1] [4] بگذارید R یک حلقه (تبادل کننده) باشد ، بگذارید G یک گروه باشد و بگذارید S یک R -algebra باشد. برای هر نوع همجنسگرایی گروهی ${\ displaystyle f: G \ to S ^ {\ بار}$ ، یک همجنسگرایی منحصر به فرد R -algebra وجود دارد $\ displaystyle {\ overline {f}}: R [G] \ to S$ به طوری که $\ displaystyle \ overline {f}} \ circ i = f$ جایی که من شامل آن هستم