ساختارهای مرتبط [ ویرایش ]

بدنه محدب متعامد

نسبی محدب محدب

چندین شکل دیگر را می توان از مجموعه ای از نقاط به شیوه ای مشابه با بدنه محدب تعریف کرد ، به عنوان حداقل سوپرست با مقداری خاصیت ، تقاطع همه اشکال حاوی نقاط از یک خانواده خاص از اشکال ، یا اتحادیه همه ترکیبات امتیاز برای نوع خاصی از ترکیب. برای مثال:

  • بدنه affine به کوچکترین فضا و affine یک فضای اقلیدسی شامل مجموعه ای داده می شود، و یا اتحادیه از تمام ترکیبات و affine از نقاط در مجموعه است. [38]
  • بدنه خطی کوچکترین فضا خطی از یک فضای برداری شامل مجموعه ای داده می شود، و یا اتحاد همه ترکیب خطی از نقاط در مجموعه است. [38]
  • بدنه مخروطی و یا بدنه مثبت یک زیر مجموعه از یک فضای برداری مجموعه ای از تمام ترکیبات مثبت از نقاط در زیر مجموعه است. [38]
  • بدنه بصری از یک شیء سه بعدی، با توجه به مجموعه ای از دیدگاه ها، متشکل از نقاطپ به گونه ای که هر پرتویی از دیدگاه از طریق آن پتقاطع شی. معادل آن تقاطع (مخروطهای غیر محدب) ایجاد شده توسط طرح کلی از جسم با توجه به هر دیدگاه است. این در بازسازی سه بعدی به عنوان بزرگترین شکل که می تواند طرح های مشابه از دیدگاه داده شده داشته باشد استفاده می شود. [39]
  • بدنه مدور یا آلفا-بدنه زیر مجموعه هواپیما تقاطع همه دیسک ها با شعاع معین است \ صفحه نمایش 1 / \ alphaکه شامل زیر مجموعه است. [40]
  • بدنه محدب نسبی از یک زیر مجموعه از دو بعدی چند ضلعی ساده تقاطع همه supersets نسبتا محدب، که در آن مجموعه ای در داخل چند ضلعی است نسبتا محدب اگر آن را شامل است متشکل از سطوح هندسی بین هر دو از نقاط آن است. [41]
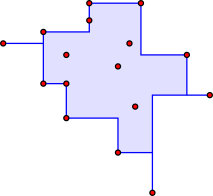
  • بدنه محدب متعامد یا بدنه محدب راست تقاطع همه supersets قائم محدب و متصل شده، که در آن مجموعه ای است قائم محدب اگر آن را شامل تمام بخش های محور موازی بین جفت از نقاط آن است. [42]
  • بدنه محدب محور متعامد یک مورد خاص از ساخت و ساز بسیار عمومی تر ، بدنه هایپرکلوکس است که می توان به عنوان کوچکترین فضای متریک تزریقی حاوی نقاط یک فضای متریک مشخص تصور کرد . [43]
  • بدنه holomorphically محدب یک کلیت از مفاهیم مشابه است manifolds پیچیده تحلیلی ، به دست آمده به عنوان یک تقاطع مجموعه زیرسطح از توابع هولومورفیک شامل مجموعه ای داده شده است. [44]

مثلث دولونه از یک مجموعه نقطه و آن دو از نمودار Voronoi ، از نظر ریاضی به پوش محدب مربوط: مثلث دولونه از مجموعه ای از نقطه در\ mathbb {R} ^ {n می توان به عنوان طرح یک قشر محدب در داخل مشاهده کرد \ \ displaystyle \ mathbb {R} ^ {n + 1.[45] اشکال آلفا از یک مجموعه نقطه محدود به یک خانواده تو در تو از (غیر محدب) اشیاء هندسی توصیف شکل یک مجموعه نقطه در سطوح مختلف از جزئیات. هر یک از شکل های آلفا ، اتحادیه برخی از ویژگی های مثلث Delaunay است ، که با مقایسه دور پرتوهای آنهابا پارامترهای آلفا انتخاب می شوند. نقطه تعیین شده ، یک نقطه پایانی از این خانواده از اشکال را تشکیل می دهد ، و شاخه محدب آن نقطه پایانی دیگر را تشکیل می دهد. [40] لایه محدب از یک مجموعه نقطه یک خانواده تو در تو از چند ضلعی محدب، دورترین که بدنه محدب، با لایه های درونی به صورت بازگشتی از نقاط که راس از بدنه محدب نیست ساخته شده است. [46]

جمجمه محدب از یک چند ضلعی است که بزرگترین محدب چند ضلعی موجود در داخل آن است. می توان آن را در زمان چند جمله ای یافت ، اما ضریب الگوریتم زیاد است. [47]

برنامه ها [ ویرایش ]

بدنه های محدب در بسیاری از زمینه ها کاربردهای گسترده ای دارند. در ریاضیات ، از حلقه های محدب برای مطالعه چند جمله ای ، مقادیر ویژه ماتریس و عناصر واحد استفاده می شود و چندین قضیه در هندسه گسسته شامل قشرهای محدب است. آنها در آمار قوی به عنوان بیرونی ترین کانتور عمق توکی مورد استفاده قرار می گیرند ، بخشی از تجسم bagplot از داده های دو بعدی هستند و مجموعه ای از ریسک قوانین تصمیم گیری تصادفی را تعریف می کنند . شاخه های محدب بردارهای نشانگر راه حل های مربوط به مشکلات ترکیبی برای بهینه سازی ترکیبی و ترکیبی های چند کلیسایی اصلی هستند.. در اقتصاد ، از حلقه های محدب می توان برای استفاده از روش های همرفت اقتصاد در بازارهای غیر محدب استفاده کرد. در مدل سازی هندسی ، منحنی های بیضی منحنی محدب به پیدا کردن تقاطع آنها کمک می کند و بدنه های محدب بخشی از اندازه گیری قایق های قایق هستند. و در مطالعه رفتار حیوانات ، از پوسته های محدب در تعریف استانداردی از محدوده خانه استفاده می شود .

https://en.wikipedia.org/wiki/Convex_hull