ادامه توابع بیضوی ژاکوبی

به طور برابر ، توابع بیضوی ژاکوبی را می توان از لحاظ عملکردهای تتا وی تعریف کرد . اگر به طور خلاصه

$\ vartheta (0؛ \ tau)$ مانند $\ vartheta$ و $\ vartheta _ {01} (0؛ \ tau)، \ vartheta _ {10} (0؛ \ tau)، \ vartheta _ {11 {(0؛ \ tau)$ به ترتیب به عنوان $\ vartheta _ {01} ، \ vartheta _ {10} ، \ vartheta _ {11$ ( ثابت تتا ) سپس مدول بیضوی k است

$k = \ سمت چپ ({\ vartheta _ {10} \ over \ vartheta} \ Right) ^ {2$ . اگر تنظیم کنیم $u = \ pi \ vartheta ^ {2} z$ ، ما داریم

$\ displaystyle {\ fill {تراز شده} \ operatorname {sn} (u؛ k) & = - {\ vartheta \ vartheta _ {11} (z؛ \ tau) \ over \ vartheta _ {10 \ vartheta _ {01 } (z؛ \ tau)} \\ [7pt] \ operatorname {cn} (u؛ k) & = {\ vartheta _ {01} \ vartheta _ {10 (z؛ \ tau) \ over \ vartheta _ { 10} \ vartheta _ {01} (z؛ \ tau)} \\ [7pt] \ operatorname {dn} (u؛ k) & = {\ vartheta _ {01} \ vartheta (z؛ \ tau) \ over \ vartheta \ vartheta _ {01} (z؛ \ tau)} \ end {تراز شده}}}$

از آنجا که توابع Jacobi از نظر مدول بیضوی تعریف شده است $k (\ tau)$ ما باید این را برعکس کنیم و پیدا کنیم $\ تاو$ به لحاظ $ک$ . ما از $k '= {\ sqrt {1-k ^ {2}}}$ ، مدول مکمل . به عنوان تابعی از $\ تاو$ این است

$k '(\ tau) = \ left ({\ vartheta _ {01} \ over \ vartheta} \ Right) ^ {2.$

بگذارید ابتدا تعریف کنیم

$\ ell = {1 \ over 2} {1 - {\ sqrt {k '}} \ over 1 + {\ sqrt {k'}}} = {1 \ over 2 {\ vartheta - \ vartheta _ {01 \ over \ vartheta + \ vartheta _ {01}.$

سپس تعریف نوم عنوان $q = \ exp (\ pi i \ tau)$ و گسترش $\ الی$ به عنوان یک سری قدرت در نام $ق$ ، ما بدست می آوریم

$\ ell = {q + q ^ {9} + q ^ {25} + \ cdots \ over 1 + 2q ^ {4} + 2q ^ {16 + \ cdots.$

بازگشت سری اکنون می دهد

$q = \ ell +2 \ ell ^ {5} +15 \ ell ^ {9} +150 \ ell ^ {13} +1707 \ ell ^ {17} +20910 \ ell ^ {21 +268616 \ ell ^ 25} + \ cdots.$

از آنجا که ما ممکن است به مواردی که قسمت تخیلی از آن می پردازیم ، کم کنیم $\ تاو$ بزرگتر از یا برابر است ${\ sqrt {3}} / 2$ ، می توانیم مقدار مطلق را فرض کنیم $ق$ کمتر از یا مساوی است $\ displaystyle \ exp (- \ pi {\ sqrt {3}} / 2) \ تقریبی 0.0658}$ ؛ برای مقادیر این سری کوچک ، سری فوق خیلی سریع همگرا می شود و به راحتی اجازه می دهد مقدار مناسب را پیدا کنیم $ق$ .

تعریف از نظر توابع نویل تتا [ ویرایش ]

توابع بیضوی ژاکوبی را می توان با استفاده از توابع تتا نوویلی بسیار ساده تعریف کرد : [4]

${\ displaystyle pq (u، m) = {\ frac {\ theta _ {p} (u، m) {\tata _ {q} (u، m)}}}$

ساده سازی محصولات پیچیده توابع بیضوی ژاکوبی اغلب با استفاده از این هویت ها آسان تر می شوند.

تحولات ژاکوبی [ ویرایش ]

تحولات تخیلی جاکوبی [ ویرایش ]

نمودار منحنی منحرف جاکوبی (x 2 + y 2 / b 2 = 1 ، b = بینهایت) و دوازده بیضوی Jacobi بیضوی pq (u، 1) برای یک مقدار خاص از زاویه φ. منحنی جامد بیضی انحطاطی است (x 2 = 1) با m = 1 و u = F (φ ، 1) که F (. ،.) انتگرال بیضوی نوع اول است .. منحنی نقطه دار دایره واحد است . از آنجا که این توابع Jacobi برای m = 0 (توابع مثلثاتی دایره ای) است اما با استدلال های تخیلی ، آنها با شش عملکرد مثلثات فشار خون بالا مطابقت دارند.

تحولات تخیلی Jacobi مربوط به توابع مختلفی از متغیر خیالی یو یا ، معادل روابط بین مقادیر مختلف پارامتر m است . از نظر کارکردهای اصلی: [5] : 506

${\ displaystyle \ operatorname {cn} (u، m) = \ operatorname {nc} (i \، u، 1 \! - \! m)$

${\ displaystyle \ operatorname {sn} (u، m) = - i \ operatorname {sc} (i \، u، 1 \! - \! m)$

${\ displaystyle \ operatorname {dn} (u، m) = \ operatorname {dc} (i \، u، 1 \! - \! m)$

با استفاده از قانون ضرب ، همه عملکردهای دیگر ممکن است براساس سه مورد فوق بیان شود. تحولات ممکن است بطور کلی نوشته شود

${\ displaystyle pq (u ، m) = \ gamma _ {pq} pq '(i \، u، 1 \! - \! m)$ . در جدول زیر آمده است

${\ displaystyle \ gamma _ {pq} pq '(i \، u، 1 \! - \! m)$ برای pq مشخص شده ( u ، m ) [4] (استدلالها $\ displaystyle (i \، u، 1 \! - \! m)$ سرکوب می شوند)

تحولات تخیلی جاکوبی $\ displaystyle \ gamma _ {pq} \ operatorname {pq} '(i \، u، 1 \! - \! m)$
		ق
		ج	s	ن	د
پ
	ج	1	من خانم	NC	دوم
	s	-یون	1	-ای SC	-سد
	ن	cn	من	1	سی دی
	د	دی ان	من Ds	دی سی	1

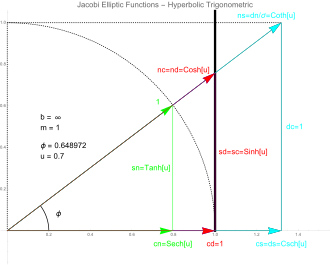
از آنجا که توابع مثلثاتی هایپربولیک متناسب با توابع مثلثاتی دایره ای با استدلال های تخیلی هستند ، نتیجه می گیرد که توابع ژاکوبی عملکرد m = 1 را به دست می آورد. [3] : 249 در شکل ، منحنی ژاکوبی به دو خط عمودی در x = 1 و x = -1 منحرف شده است .

تحولات واقعی ژاکوبی [ ویرایش ]

تحولات واقعی ژاکوبی [3] : 308 عبارات عملکرد بیضوی را از نظر مقادیر متناوب از متر . تحولات ممکن است بطور کلی نوشته شود ${\ displaystyle pq (u ، m) = \ gamma _ {pq} pq '(k \، u، 1 / m)}$ . در جدول زیر آمده است ${\ displaystyle \ gamma _ {pq} pq '(k \، u، 1 / m)}$ برای pq مشخص شده ( u ، m ) [4] ${\ displaystyle (k \ ، u ، 1 / m)}$ سرکوب می شوند)

تحولات واقعی جاکوبی ${\ displaystyle \ gamma _ {pq} \ operatorname {pq} '(k \، u، 1 / m)$
		ق
		ج	s	ن	د
پ
	ج	1	$ک$ DS	دی ان	دی سی
	s	$\ frac {1} {k}}$ SD	1	$\ frac {1} {k}}$ اسن	$\ frac {1} {k}}$ SC
	ن	دوم	$ک$ ns	1	NC
	د	سی دی	$ک$ سی سی	cn	1

سایر تحولات ژاکوبی [ ویرایش ]

تحولات واقعی و تخیلی جاکوبی را می توان با روش های مختلفی ترکیب کرد تا سه دگرگونی ساده دیگر حاصل شود. [3] : 214 تحولات واقعی و تخیلی دو تحول در یک گروه (گروه D 3 یا Anharmonic ) شش تحول است. اگر

$\ displaystyle \ mu _ {R} (m) = 1 / m$

تبدیل برای پارامتر m در تحول واقعی ، و

$\ displaystyle \ mu _ {I} (m) = 1-m = m '$

تحول m در تحول خیالی است ، پس از آن با استفاده مداوم از این دو دگرگونی اساسی ، می توان دگرگونی های دیگر ایجاد کرد و تنها سه امکان دیگر داشت:

$\ displaystyle {\ شروع {تراز شده} \ mu _ {IR} (m) & = & \ mu _ {I} (\ mu _ {R} (m)) & = & - - m '/ m \\\ mu _ {RI} (m) & = & \ mu _ {R} (\ mu _ {I} (m)) & = & 1 / m '\\\ mu _ {RIR} (m) & = & & mu- {R} (\ mu _ {I} (\ mu _ {R} (m))) & = & - m / m '\ end {تراز شده}}$

این پنج تحول ، همراه با تحول هویت (μ U (m) = m) گروه 6 عنصر را به همراه دارند. با توجه به توابع بیضوی ژاکوبی ، تحول کلی می تواند فقط با سه کارکرد بیان شود:

${\ displaystyle \ operatorname {cs} (u، m) = \ gamma _ {i} \ operatorname {cs '} (\ gamma _ {i} u، \ mu _ {i} (m))$

${\ displaystyle \ operatorname {ns} (u، m) = \ gamma _ {i} \ operatorname {ns '} (\ gamma _ {i} u، \ mu _ {i} (m))$

${\ displaystyle \ operatorname {ds} (u، m) = \ gamma _ {i} \ operatorname {ds '} (\ gamma _ {i} u، \ mu _ {i} (m))$

که در آن i = U، I، IR، R، RI یا RIR با مشخص کردن تبدیل ، γ i یک عامل ضرب مشترک برای این سه عملکرد است و نخست نشان دهنده عملکرد تبدیل شده است. 9 عملکرد دیگر تبدیل شده از سه مورد فوق قابل ساخت است. دلیل انتخاب توابع cs ، ns ، ds برای نشان دادن تحول این است که سایر توابع نسبت این سه (به جز وارونهای آنها) خواهند بود و عوامل ضرب لغو خواهد شد.

در جدول زیر عوامل ضرب سه تابع ps ، m تبدیل شده و نام تابع تبدیل شده برای هر یک از شش تبدیل ذکر شده است. [3] : 214 (طبق معمول ، k 2 = m ، 1-k 2 = k 1 2 = m 'و آرگومان ها () $\ displaystyle \ gamma _ {i} u، \ mu _ {i} (m)$ ) سرکوب می شوند)

پارامترهای شش تحول
تحول i	$\ گاما _ {من}$	$\ displaystyle \ mu _ {i} (m)$	cs '	ns '	DS '
t	1	م	سی سی	ns	DS
i	من	من	ns	سی سی	DS
IR	ik	-م '/ متر	DS	سی سی	ns
ر	ک	1 / متر	DS	ns	سی سی
RI	ik 1	1 / متر '	ns	DS	سی سی
RIR	k 1	-م / متر	سی سی	DS	ns

به عنوان مثال ، ممکن است جدول زیر را برای تبدیل RIR بسازیم. [4] تحول به طور کلی نوشته شده است

${\ displaystyle \ operatorname {pq} (u، m) = \ gamma _ {pq} \، \ operatorname {pq '} (k' \، u، -m / m ')}$ (استدلالها ${\ displaystyle (k '\، u ، -m / m')}$ سرکوب می شوند)

$\ displaystyle \ gamma _ {pq} \، \ operatorname {pq '} (k' \، u، -m / m ')}$
		ق
		ج	s	ن	د
پ
	ج	1	Ks	سی دی	cn
	s	$\ frac {1} {k '}}$ SC	1	$\ frac {1} {k '}}$ SD	$\ displaystyle {\ frac {1} {k '}}}$ اسن
	ن	دی سی	$k '$ DS	1	دی ان
	د	NC	$k '$ ns	دوم	1

مقدار تحولات Jacobi به این صورت است که هر مجموعه ای از توابع بیضوی Jacobi با هر پارامتر m -Value پیچیده را می توان به مجموعه دیگری تبدیل کرد که برای آن 0 <= m <= 1 و برای مقادیر واقعی u ، مقادیر عملکرد واقعی خواهند بود. . [3] : ص.215

hyperbola ژاکوبی [ ویرایش ]

طرح ابرقابل جکوبی ( x 2 + y 2 / b 2 = 1 ، b تخیلی) و دوازده بیضوی Jacobi بیضوی pq (u ، m) برای مقادیر خاص زاویه φ و پارامتر b . منحنی جامد هذلولی با، متر = 1-1 / ب 2 و تو = F (φ، متر) که در آن F (.،.) است جدایی ناپذیر بیضوی از نوع اول است. منحنی نقطه دار دایره واحد است. برای مثلث( ds-dc ، σ = Sin (φ) Cos (φ .

با ارائه اعداد پیچیده ، بیضه ما دارای یک ابرقابل همراه است:

$\ displaystyle xx ^ {2} - {\ frac {yy ^ {2}} {b ^ {2}}} = 1$

از اعمال تحول تخیل ژاکوبی [4] به توابع بیضوی در معادله فوق برای x و y .

${\ displaystyle xx = {\ frac {1} {\ operatorname {dn} (u، 1-m)}}، \ quad yy = {\ frac {\ operatorname {sn} (u، 1-m)} {\ operatorname {dn} (تو ، 1 متر)}}}$

این نتیجه می گیرد که می توانیم قرار دهیم ${\ displaystyle x = \ operatorname {dn} (تو ، 1 متر) ، y = \ operatorname {sn} (تو ، 1 متر)$ . بنابراین بیضی ما یک بیضی دوتایی دارد با m جایگزین 1 متر می شود. این منجر به توروس پیچیده ای شده که در مقدمه ذکر شده است. [6] به طور کلی ، m ممکن است عدد پیچیده ای باشد ، اما هنگامی که m واقعی باشد و m <0 ، منحنی یک بیضی با محور اصلی در جهت x است. در m = 0 منحنی یک دایره است و برای 0 1 ، منحنی یک hyperbola است. وقتی متر پیچیده اما واقعی نیست ، x یا y یا هر دو پیچیده هستند و منحنی را نمی توان در یک نمودار xy واقعی توصیف کرد.

منبع

https://en.wikipedia.org/wiki/Jacobi_elliptic_functions

+ نوشته شده در شنبه چهارم مرداد ۱۳۹۹ ساعت 7:32 توسط علی رضا نقش نیلچی |

ریاضیات

آموزش ریاضی