
حل cos x = x ^3 [ ویرایش ]
مشکل پیدا کردن تعداد مثبت x با cos x = x^ 3 را در نظر بگیرید. ما می توانیم به عنوان پیدا کردن صفر از
f ( x ) = cos ( x ) - x ^3 دوباره بیان کنیم . ماf ' ( x ) = -sin ( x ) - 3 x^ 2 داریم . از آنجا که
cos ( x ) ≤ 1 برای همه x و x 3 > 1 برای x > 1 ، ما می دانیم که راه حل ما بین 0 و 1 است. ما یک مقدار شروعx 0 = 0.5 را امتحان می کنیم. (توجه داشته باشید که مقدار شروع از 0 منجر به نتیجه نامشخصی خواهد شد، نشان دهنده اهمیت استفاده از نقطه شروع است که نزدیک به راه حل است.)
تهران– ایرنا- رئیس انجمن سیستم های فازی گفت: بر اساس اعلام پایگاه 'اسكوپوس'، جمهوری اسلامی ایران طی سال های 2013 و 2014 میلادی و به احتمال زیاد 2015، مقام سوم جهان را در نظریه سیستم های فازی كسب كرد.
به گزارش خبرنگار علمی ایرنا ، محمدمهدی زاهدی روز سه شنبه در مراسم نكوداشت پروفسور لطفی زاده در دانشكده فنی دانشگاه تهران افزود: مقام اول و دوم به ترتیب در اختیار كشور چین و هند است.
كارشناسان نظریه فازی را موجد انقلابی بزرگ در بخش های مختلف علمی و فناوری دنیا به ویژه در حوزه های فنی و مهندسی، علوم كامپیوتر، ریاضیات، مدیریت، پزشكی، صنایع هوایی، كشاورزی و غیره می دانند و معتقدند سیستم های فازی به نوعی منطق دو ارزشی، درست و غلط، زشت و زیبا و سفید و سیاه را كنار گذاشته است و دنیای واقعی را با یك مدل ریاضی، یك دنیای خاكستری و میان صفر و یك، سفید و سیاه و درست و غلط توصیف می كند كه این تفكر اكنون در تمام پدیده های جهان به نوعی موثر شده است. هواپیماهای در حال تولیدی كه كاملا اتو پایلوت و با منطق فازی كار می كنند، از دستاوردهای این حوزه و هوش مصنوعی از دیگر كاربست های ان است.
** پروفسور لطفی زاده از تبار دانشمندان برتر ایرانی
زاهدی همچنین اظهار كرد: تاریخ و تمدن ایران اسلامی نشان از آن دارد كه این سرزمین مهد تربیت و تحویل دانشمندان زیادی از جمله بوعلی سینا، خوارزمی، فارابی و زكریای رازی به جامعه بشری بوده است.
وی ادامه داد: جای تعجب نیست كه امروز لطفی زاده را گرامی می داریم و این مراسم را برگزار می كنیم، چراكه او از سلسله دانشمندان برتر ایرانی است. این دانشمند بزرگ ایرانی نقش اساسی در عرصه علم و فناوری و كاربردی كردن نظریه سیستم های فازی داشته است و می توان او را به عنوان یك الگوی كامل به تمام دانش پژوهان به خصوص جوانان معرفی كرد.
رییس انجمن سیستم های فازی ایران ادامه داد: لطفی زاده موفق به دریافت 9 مدال علمی، 14 جایزه علمی و 24 دكترای افتخاری از موسسات و دانشگاه های معتبر جهانی شده است. تاكنون نزدیك به 111 هزار مقاله علمی توسط دانشمندان و محققان حوزه منطق و سیستم های فازی در مجلات معتبر به چاپ رسیده كه با توجه به حدود 50 ساله ارائه نظریه ایشان، این تعداد بسیار زیاد است.
زاهدی افزود: لطفی زاده علاقه زیادی به دانشجویان ایرانی داشته و از این رو همت فراوانی برای تربیت علمی این افراد به كاربرده است كه نتیجه آن را در محافل علمی دنیا مشاهده می كنیم.
وی گفت: ما باید از این همت و تلاش درس بگیریم تا بتوانیم نسل جدید را متكی به خود، خلاق، نوآور و محقق تربیت كنیم تا با استفاده از توان و ظرفیت آنها شاهد توسعه و پیشرفت كشور باشیم.
پروفسور لطفی زاده در سال 1229 شمسی برابر با 1921 میلادی از یك پدر روزنامه نگار ایرانی و یك مادر پزشك روسی در شهر باكو جمهوری آذربایجان به دنیا آمد.
وی در 10 سالگی به همراه خانواده به خانه پدری اش به ایران بازگشت و در تهران ساكن شد.
لطفی زاده در سال 1320 با اخذ مدرك لیسانس در رشته برق و الكترونیك دانشگاه تهران فارغ التحصیل شد و دوره فوق لیسانس مهندسی برق را در انستیتوی تكنولوژی ماساچوست آمریكا شروع كرد و در نهایت در سال 1327 شمسی مدرك دكتری خود را از دانشگاه كلمبیا دریافت كرد.
پس از آن پروفسور لطفی زاده در همان دانشگاه تحقیقات خود را در زمینه نظریه سیستم ها آغاز كرده و سپس در سال 1334 شمسی به عنوان پژوهشگر به مركز مطالعات پیشرفته پرینستون دعوت شد.
پروفسور لطفی زاده كه مشاغل علمی و عضویت های افتخاری موسسات متعددی را پذیرفته است، به عنوان كاشف و مبتكر منطق فازی شهرت جهانی دارد.
وی كه در جهان علم به �پروفسور زاده� معروف است، طی یك مقاله علمی كلاسیك كه در سال ۱۳۴۳ به چاپ رسید، مفهوم مجموعه فازی را كه مبتنی بر تئوری تجزیه و تحلیل سیستم های پیچیده است، بر اساس زبان طبیعی معرفی كرد.
پس از معرفی تئوری فازی، بیش از ۱۱۱ هزار مقاله علمی توسط دانشمندان جهان درباره منطق فازی و كاربردهای گسترده ی آن در نشریات علمی منتشر شده و در حدود هزار درخواست ثبت اختراع در این زمینه در ژاپن و سایر كشورهای مختلف جهان به عمل آمده است.
تنها در ژاپن، بیش از دو هزار دانشمند روی منطق فازی و سیستم های مبتنی بر آن كار می كنند. نظریه لطفی زاده اكنون دیگر محدود به ریاضیات و مهندسی نمانده و بسیاری از اندیشه ها و تفكرات فازی را كه از صدها سال پیش در ذهن بشر مطرح بوده، دوباره در ابعادی جهانی برای انسان معاصر مطرح كرده است.
از ویکیپدیا، دانشنامه آزاد
مقایسه ی گرادیان فرود (سبز) و روش نیوتن (قرمز) برای به حداقل رساندن یک تابع (با اندازه های کوچک گام). روش نیوتن از اطلاعات انحرافی (یعنی مشتق دوم) استفاده می کند تا یک مسیر مستقیم تر را بگیرد.
در محاسبه ، روش نیوتن یک روش تکراری برای یافتن ریشه یک تابع متمایز f است که راه حل معادله f ( x ) = 0 است . در بهینه سازی، روش نیوتن به اعمال مشتق f را ، از یک تابع دو بار مشتقپذیر F پیدا کردن ریشه های مشتق شده (راه حل برای F ( X ) = 0 )، همچنین به عنوان شناخته شده نقاط ثابت از F. این راه حل ها ممکن است حداقل، حداکثر یا نقاط زین باشد. [ نیازمند منبع ]
فهرست
روش [ ویرایش ]
در مساله یک بعدی، روش نیوتن تلاش برای پیدا کردن ریشه های F ، با احداث یک توالی X N از یک حدس اولیه X 0 که به سمت برخی از ارزش همگرا X * رضایت F '( X * ) = 0 . این X * است نقطه ثابت از F .
توزیع ثانویه تیلور f T ( x ) یک تابع f در اطراف x n است
در حالت ایده آل، ما می خواهیم به انتخاب یک Δ X که X N + Δ X است نقطه ثابت از F . با استفاده از گسترش تیلور به عنوان یک تقریب، می توانیم حداقل برای Δ x مطابقت با ریشه مشتق گسترش را حل کنیم:
ارائه تقریب تیلور نسبتا دقیق، سپس با بالا افزایش Δ X باید یک نقطه نسبتا نزدیک به یک نقطه ثابت واقعی عملکرد ج . این نقطه، X N 1 = X N + Δ X = X N - F '( x را N ) / F "( X N ) ، تعریف ما این بود که N + 1 حدس هفتم در روش نیوتن؛ به عنوان n به سمت بی نهایت، x n باید یک نقطه ثابت x *از عملکرد واقعی f . در حقیقت ثابت شده است که اگر f یک تابع دو بار تفاضلی باشد و سایر شرایط فنی راضی باشد، دنباله x 1 ، x 2 ، ... به یک نقطه x * که f '( x * ) = 0 را می پذیرد، همگرایی می کند . [ نیازمند منبع ]
تفسیر هندسی [ ویرایش ]
تفسیر هندسی از روش نیوتن این است که در هر تکرار، آن را به اتصالات از یک مقدار قطع مخروطی به سطح از F ( X ) در ارزش محاکمه X N ، داشتن دامنه همان و انحنای به عنوان سطح در آن نقطه، و پس از آن به دنبال حداکثر یا حداقل آن پارابولید (در ابعاد بالاتر، این ممکن است یک نقطه ی زاویه باشد ). [1] توجه داشته باشید که اگر F ( X ) اتفاق می افتد به می شود یک تابع درجه دوم، پس از آن حد اکثر دقیق، در یک گام در بر داشت.
ابعاد بالاتر [ ویرایش ]
بالا طرح تکراری را می توان به ابعاد مختلف با جایگزین کردن مشتق با تعمیم شیب ، ∇ F ( X ) ، و متقابل از مشتق دوم با معکوس از ماتریس هشین ، H F ( X ) . یک طرح تکراری به دست می آید
اغلب روش نیوتن اصلاح شده است که شامل یک گام کوچک کوچک γ ∈ (0،1) به جای γ = 1 است
این اغلب برای اطمینان از این که شرایط ولف در هر مرحله x n → x n +1 تکرار می شود انجام می شود. برای اندازه گام های غیر از 1، روش اغلب به عنوان روش نیوتن آرام است.
در جایی که قابل استفاده است، روش نیوتن بسیار سریعتر به سمت حداکثر یا حداقل حداکثر از زادگاه گرادینت همگرایی می کند . در حقیقت، هر حداقل محلی دارای محور N است به طوری که اگر ما با x 0 ∈ N شروع کنیم ، روش نیوتن با اندازه گام γ = 1 همگرا به صورت چهارگانه (اگر Hessian یک معکوس باشد و یک تابع Continuous Lipschitz از x در آن محله).
پیدا کردن معکوس Hessian در ابعاد بزرگ می تواند یک عملیات گران قیمت باشد. در چنین مواردی، به جای مستقیم Hessian، بهتر است بردار Δ x = x n + 1 - x n را به عنوان راه حل برایسیستم معادلات خطی محاسبه کنیم
که ممکن است با تقسیم بندی های مختلف یا تقریبا (اما به دقت زیادی) با استفاده از روش های تکراری حل شود . بسیاری از این روش ها فقط برای انواع خاصی از معادلات قابل استفاده هستند، به عنوان مثال فاکتورهای Cholesky و گرادیان کنجوات فقط اگر [ H f ( x n )] یک ماتریس قطعی مثبت باشد. در حالی که این ممکن است بعنوان یک محدودیت ظاهر شود، اغلب نشانگر مفیدی از چیزی است که اشتباه رفته است؛ به عنوان مثال اگر یک مشکل کمینه سازی در حال نزدیک شدن است و [ H f ( x n )] قطعی مثبت نیست، سپس تکرار به یک نقطه ی زاویه همگرایی و نه حداقل.
از سوی دیگر، اگر یک بهینه سازی محدود شده انجام شود (به عنوان مثال، با ضرایب Lagrange )، مسئله ممکن است یکی از نقطه ی نقطه ی زاویه باشد؛ در این صورت Hessian نامشخص متقارن خواهد بود و راه حل x n +1 نیاز به با یک روش که برای چنین کارهایی مانند نوع LDL T فاکتوریزه Cholesky یا روش باقی مانده همگانی کار می کند، انجام می شود .
همچنین روش های مختلف شبه نیوتن وجود دارد که در آن تقریبی برای هسیان (یا معکوس آن به طور مستقیم) از تغییرات شیب ساخته شده است.
اگر Hessian نزدیک به یک ماتریس غیر قابل برگشت باشد ، Hessian معکوس می تواند عددی ناپایدار باشد و راه حل ممکن است متفاوت باشد. در این مورد، راه حل های خاصی در گذشته مورد آزمایش قرار گرفته است، که با مشکلات خاصی در حال تغییر است. برای مثال، می توان Hessian را با اضافه کردن یک ماتریس اصلاح B n به صورت H f ( x n ) + B n مثبت تعیین کرد. یکی از رویکردهای این است که H f ( x n ) را بطور مداوم و B n بگذاریم تا H f ( x n ) + Bn همان ويژگي هاي ويژه همانند H f ( x n ) دارد، اما با هر مقدار ويژه منفي توسطε> 0تعويض مي شود.
یک رویکرد بهره برداری شده در الگوریتم Levenberg-Marquardt (که از یک Hessian تقریبی استفاده می کند) این است که ماتریس هویت مقیاس را به Hessian، μ I اضافه کرده و مقیاس را در هر تکرار در صورت نیاز تنظیم کند. برای μ بزرگ و کوچک Hessian، تکرارها به صورت شیب گرادیان با اندازه گام 1 / μ رفتار خواهند کرد. این نتیجه همگرایی کندتر، اما قابل اطمینان تر است که Hessian اطلاعات مفیدی را ارائه نمی دهد.
همچنین نگاه کنید به [ ویرایش ]
از ویکیپدیا، دانشنامه آزاد
حداقل درخت پوشا از وزن گراف مسطح . پیدا کردن حداقل درخت درختی یک مشکل رایج در بهینه سازی ترکیبی است.
در تحقیقات عملیاتی ، ریاضی کاربردی و علوم رایانه نظری ، بهینه سازی ترکیبی موضوعی است که شامل یافتن شیء بهینه از یک مجموعه محدود از اشیاء است. [1] در بسیاری از چنین مشکلی، جستجوی جامع قابل ردیابی نیست. آن را بر روی دامنه از این مشکلات بهینه سازی، که در آن مجموعه ای از عمل راه حل های عملی است گسسته و یا می توان کاهش داد گسسته، و در آن هدف این است که برای پیدا کردن بهترین راه حل. برخی از مشکلات رایج در بهینه سازی ترکیبی عبارتند از مشکل فروشندگان مسافر (TSP)،مشکل حداقل درخت درخت (MST) و مشکل حلقه .
بهینه سازی ترکیبی یک زیرمجموعه بهینه سازی ریاضی است که مربوط به تحقیقات عملیاتی ، نظریه الگوریتم و نظریه پیچیدگی محاسباتی است . این برنامه کاربردی مهم در زمینه های مختلف از جمله هوش مصنوعی ، یادگیری ماشین ، نظریه حراج و مهندسی نرم افزار است .
برخی ادبیات تحقیق [2] نظر بهینه سازی گسسته شده شامل برنامه ریزی عدد صحیح همراه با بهینه سازی ترکیبی (که به نوبه خود متشکل از مسائل بهینه سازی با ساختار نمودار این حال تمامی این موضوعات در هم تنیده ادبیات تحقیق). این اغلب شامل تعیین راه برای به طور موثر تخصیص منابع مورد استفاده برای یافتن راه حل مشکلات ریاضی است.
فهرست
برنامه های کاربردی [ ویرایش ]
برنامه های کاربردی برای بهینه سازی ترکیبی شامل، اما نه محدود به:
توسعه بهترین شبکه هواپیمایی اسکواش و مقصد
تصمیم بگیرید که تاکسی در ناوگان برای رسیدن به کرایه بلیط
تعیین راه بهینه برای ارائه بسته ها
بهترین تخصیص شغل به مردم را بسازید
تعیین صحیح عناصر مفهومی قبل از تست مفهوم [ نیازمند منبع ]
روشها [ ویرایش ]
تعداد زیادی از ادبیات در مورد الگوریتم های چندجملهای زمان برای کلاس های خاصی از بهینه سازی گسسته وجود دارد، مقدار قابل توجهی از آن توسط تئوری برنامه نویسی خطی یکپارچه شده است .برخی از نمونه هایی از مشکلات بهینه سازی ترکیبی که در این چارچوب قرار می گیرند کوتاه ترین مسیر ها و درختان کوتاه ترین مسیر ، جریان ها و گردش ، درختان درختی ، تطبیق و مشکلاتMatroid هستند.
برای مسائل بهینه سازی گسسته NP- کامل ، مقالات پژوهشی تحقیقاتی شامل موضوعات زیر است:
چند جمله ای زمان دقیقا قابل حل موارد خاصی از مشکل در دست (به عنوان مثال نمایش ثابت ثابت قابل ردیابی )
الگوریتم هایی که در موارد "تصادفی" خوب عمل می کنند (مثلا برای TSP )
الگوریتم های تقریبی که در زمان چندجملهای اجرا می شوند و یک راه حل را پیدا می کنند که نزدیک به مطلوب است
حل پرونده های دنیای واقعی که در عمل بوجود می آیند و الزاما رفتار بدترین حالت را در ذاتی مشکلات NP کامل نشان نمی دهند (مثلا نمونه های TSP با ده ها هزار گره [5] ).
مشکلات بهینه سازی ترکیبی را می توان به عنوان جستجو برای بهترین عنصر از برخی از مجموعه ای از اقلام گسسته؛ بنابراین، در اصل، هر گونه الگوریتم جستجو یا متاگیریستی می تواند مورد استفاده قرار گیرد برای حل آنها. با این حال، الگوریتم های جستجوی عمومی برای رسیدن به یک راه حل مطلوب تضمین نمی شوند و همچنین تضمین می شود که به سرعت (در زمان چندجملهای) اجرا شود. از آنجایی که برخی از مشکلات بهینه سازی گسسته NP-complete ، مانند مشکل فروش فروشنده [ نیازمند استناد ] هستند ، این انتظار می رود مگر اینکه P = NP .
تعریف رسمی [ ویرایش ]
به طور رسمی یک مشکل بهینه سازی ترکیبی است 

یک مجموعه ای از نمونه؛
با توجه به نمونه
مجموعه ای از راه حل های قابل اجرا است.
با توجه به نمونه
و یک راه حل امکان پذیر است
از
نشان دهنده اندازه گیری از که معمولا مثبت واقعی است .
تابع هدف است و یا
یا
هدف این است که برای برخی از نمونه ها پیدا شود {\ displaystyle x}

برای هر یک از مسائل بهینه سازی ترکیبی، یک مسئله تصمیم مربوطه وجود دارد که می پرسد آیا یک راه حل قابل قبول برای یک اندازه گیری خاص وجود دارد{\ displaystyle m_ {0}}







در زمینه الگوریتم های تقریبی ، الگوریتم ها برای یافتن راه حل های نزدیک به مطلوب برای مشکلات سخت طراحی شده اند. نسخه معمولی تصمیم گیری یک تعریف ناکافی از مشکل است، زیرا تنها راه حل های قابل قبول را مشخص می کند. اگر چه ما می توانیم مشکلات تصمیم گیری مناسب را معرفی کنیم، مشکل به طور طبیعی به عنوان یک مشکل بهینه سازی مشخص می شود. [6]
مشکل بهینه سازی NP [ ویرایش ]
یک مشکل بهینه سازی NP (NPO) یک مشکل بهینه سازی ترکیبی با شرایط اضافی زیر است. [7] توجه داشته باشید که چندجمله ای زیر اشاره توابع از اندازه ورودی های توابع مربوطه، نه اندازه برخی از مجموعه ضمنی از نمونه های ورودی است.
این بدان معنی است که مسئله تصمیم مربوطه در NP است . در علم کامپیوتر، مشکلات بهینه سازی جالب معمولا دارای ویژگی های بالا هستند و بنابراین مشکلات NPO هستند. اگر یک الگوریتم وجود داشته باشد که یک راه حل بهینه در زمان چند جمله ای پیدا می کند، مشکل دیگری نیز به نام P-optimization (PO) است. اغلب هنگام برخورد با NPO کلاس، یک فرد علاقه مند به مشکلات بهینه سازی است که نسخه های تصمیم گیری NP-complete هستند . توجه داشته باشید که روابط سختی همیشه با توجه به برخی از کاهش است. با توجه به ارتباط بین الگوریتم های تقریبی و مسائل بهینه سازی محاسباتی، کاهش هایی که تقریبا در برخی موارد احترام می گذارند، برای این موضوع ترجیح داده شده است از کاهش معمول تورینگ و کارپ. یک مثال از این کاهش می تواندکاهش L باشد. به همین دلیل، مشکلات بهینه سازی با نسخه های تصمیم گیری کامل NP-NP لزوما NPO کامل نیستند. [8]
NPO با توجه به تقریب پذیر بودن آنها به زیر کلاس های زیر تقسیم می شود: [7]
NPO (I) : برابر FPTAS . شامل مشکل Knapsack است .
NPO (II) : برابر با PTAS . شامل برنامه زمانبندی Mackpan است.
NPO (III) :: کلاسهای مشکلات NPO که دارای الگوریتم های چندجملهای هستند که راه حل هایی را با هزینه ای که بیشتر از c برابر هزینه های بهینه (برای مشکلات کمینه سازی) و یا حداقل هزینه
از هزینه بهینه (برای مسائل به حداکثر رساندن). در کتاب Hromkovič ، از این کلاس حذف می شوند، تمام NPO (II) -problems صرف نظر اگر P = NP. بدون محرومیت، برابر با APX است. شامل MAX-SAT و TSP متریک .
NPO (IV) :: کلاس های مشکلات NPO با الگوریتم های چندجمله ای زمان تقریبی راه حل بهینه با نسبت است که چندجملهای در یک لگاریتم اندازه ورودی است. در کتاب Hromkovic، تمام مشکلات NPO (III) از این کلاس حذف می شوند مگر اینکه P = NP. شامل مشکل پوشش مجموعه است.
NPO (V) :: کلاس های مشکلات NPO با الگوریتم های چندجمله ای تقریبأ راه حل بهینه را با نسبت محدود شده توسط برخی از تابع در n. در کتاب Hromkovic، تمام مشکلات NPO (IV) از این کلاس حذف می شوند مگر اینکه P = NP. شامل مشکلات TSP و Max Clique است .
یک مشکل NPO به طور چندجملهای محدود (PB) نامیده می شود، اگر برای هر مورد


مشکلات خاص [ ویرایش ]
سفر توریستی مسافرتی به بهترین سفر در 15 کشور بزرگ آلمان . این کوتاهترین در میان 43،589،145،600 [9] تورهای ممکن است که فقط یک بار از هر شهر بازدید می کنند.
از ویکیپدیا، دانشنامه آزاد
در ریاضیات ، برنامه نویسی غیر خطی ( NLP ) فرایند حل یک مشکل بهینه سازی است که برخی از محدودیت ها یا تابع هدف غیر خطی هستند . مسئله بهینه سازی یکی از محاسبه اکسترمم (حداکثر، حداقل و یا نقاط ثابت) از یک است تابع هدف بیش از مجموعه ای از ناشناخته متغیرهای حقیقی و مشروط به رضایت از سیستم از برابری و نابرابری ، نامیده می شوند محدودیت . [1] این زیر زمینهبهینه سازی ریاضی است که با مشکلاتی روبرو می شود که خطی نیستند.
فهرست
- 1قابل اجرا بودن
- 2تعریف
- 3انواع احتمالی مجموعه محدودیت
- 4روش برای حل مشکل
- 5نمونه
- 6همچنین ببینید
- 7منابع
- 8خواندن بیشتر
- 9پیوندهای خارجی
کاربردی [ ویرایش ]
یک مشکل غیر مسطح معمول این است که بهینه سازی هزینه های حمل و نقل با انتخاب از مجموعه ای از روش های حمل و نقل، که یکی یا بیشتر از آنها دارای مقیاس های اقتصادی ، با اتصالات مختلف و محدودیت های ظرفیت است. یک مثال میتواند حمل و نقل محصولات نفتی با انتخاب یا ترکیبی از خطوط لوله، تانکرهای ریلی، تانکرهای تانکر، بارج رودخانه یا تانکهای ساحلی باشد. با توجه به اندازه دسته ای اقتصادی، توابع هزینه ممکن است علاوه بر تغییرات صاف، اختلال ایجاد کند.
در علم تجربی، برخی از داده های ساده تجزیه و تحلیل (مانند اتصالات طیف با مجموع قله های مکان و شکل شناخته شده، اما ناشناخته) می تواند با روش های خطی انجام شود، اما به طور کلی این مشکلات نیز غیر خطی هستند. به طور معمول، یک مدل نظری از سیستم مورد مطالعه با پارامترهای متغیر در آن وجود دارد و یک مدل آزمایش یا آزمایش است که ممکن است پارامترهای ناشناخته نیز داشته باشد. یکی تلاش می کند تا بهترین عدد را پیدا کند. در این مورد، اغلب می خواهد اندازه گیری دقیق نتیجه، و همچنین بهترین مناسب خود را.
تعریف [ ویرایش ]
اجازه دهید n ، m ، و p عدد صحیح مثبت باشند. اجازه دهید X می شود زیر مجموعه R N ، اجازه دهید F ، G من ، و ساعت J شود توابع حقیقی در X برای هر من در { 1 ، ...، متر } و هر Jدر { 1 ، ...، ص }، با در حداقل یکی از f ، g i ، و h j غیر خطی است.
مشکل کمینه سازی غیر خطی یک مشکل بهینه سازی فرم است
یک مشکل حداکثری غیر خطی به روش مشابهی تعریف شده است.
انواع مختلف مجموعه محدودیت [ ویرایش ]
چندین ویژگی برای ماهیت مجموعه محدودیت وجود دارد، که همچنین به عنوان منطق عملی یا منطقی امکان پذیر است .
یک مشکل نامطلوب است که برای آن هیچ مجموعه ای از مقادیر برای متغیرهای انتخاب مناسب تمام محدودیت ها نیست. به این معناست که محدودیتها متقابلا متناقض است و هیچ راه حلی وجود ندارد؛مجموعه عملی مجموعه خالی است .
امکان پذیر مشکل که برای آن وجود دارد حداقل یک مجموعه ای از ارزش برای متغیرهای انتخاب رضایت تمام محدودیت وجود دارد.
یک مشکل بی حد و حصر ، یک مشکل قابل اجرا است که می توان آن را تابع هدف را بهتر از هر مقدار معین شده دانست. به این ترتیب هیچ راه حل مطلوبی وجود ندارد، زیرا همیشه یک راه حل امکان پذیر است که ارزش تابع هدف بهتر را نسبت به هر راه حل پیشنهادی ارائه می دهد.
روش های حل مشکل [ ویرایش ]
اگر تابع هدف f به خطی است و محدود فضای یک چندبر ، مشکل است برنامه ریزی خطی مشکل، که ممکن است با استفاده از تکنیک برنامه ریزی خطی شناخته شده مانند حل روش سیمپلکس .
اگر تابع هدف مقعر باشد (مشکل حداکثر سازی) یا محدب (مشکل کمینه سازی) و مجموعه محدودیت محدب است ، سپس برنامه به صورت محدب نامیده می شود و روش های عمومی از بهینه سازی محدب در بیشتر موارد استفاده می شود.
اگر تابع هدف دوم درجه دوم باشد و محدودیت ها خطی باشند، تکنیک های برنامه ریزی درجه دوم استفاده می شود.
اگر تابع هدف یک نسبت یک تابع مقعر و یک محدب باشد (در مورد حداکثر سازی) و محدودیت ها محدب هستند، پس مشکل را می توان به یک مشکل بهینه سازی محدب با استفاده از تکنیک هایبرنامه ریزی کسری تبدیل کرد .
چند راه حل برای حل مشکلات غیرقابل دسترس وجود دارد. یک رویکرد این است که از فرمول خاصی برای مشکلات برنامه نویسی خطی استفاده شود. روش دیگر شامل استفاده از شاخه و محدود استتکنیک ها، جایی که برنامه به زیر کلاس ها تقسیم می شود تا با محدب (مشکل کمینه سازی) یا تقریب خطی حل شوند که هزینه کمتری را در زیر بخش تقسیم می کنند. با تقسیمات بعدی، در برخی موارد یک راه حل واقعی به دست خواهد آمد که هزینه آن برابر با بهترین حد پایین برای هر یک از راه حل های تقریبی است. این راه حل مطلوب است، گرچه احتمالا منحصر به فرد نیست. الگوریتم نیز ممکن است در اوایل متوقف شود، با اطمینان که بهترین راه حل ممکن است در تحمل از بهترین نقطه پیدا شود؛ چنین نقاط ε-optimum نامیده می شوند. به طور کلی برای تضمین محدود شدن محدودیت ها، پایان دادن به نقاط ε-optimum ضروری است. این به خصوص برای بزرگ،
تحت شرایط تمایز و محدودیت ، شرایط Karush-Kuhn-Tucker (KKT) شرایط لازم را برای یک راه حل برای بهینه فراهم می کند. تحت محدوده، این شرایط نیز کافی است. اگر برخی از توابع غیر غیر قابل تفکیک باشند، نسخه های دوبعدی شرایط Karush-Kuhn-Tucker (KKT) در دسترس هستند. [2]
مثالها [ ویرایش ]
مثال 2 بعدی [ ویرایش ]
منطقه آبی منطقه قابل اجرا است . خط تیرهخط با منطقه قابل اجرا نشان دهنده راه حل است. خط بهترین خط کانونی قابل دستیابی است (منطق با مقدار مشخصی از تابع هدف).
یک مشکل ساده (نشان داده شده در نمودار) می تواند توسط محدودیت ها تعریف شود
x 1 ≥ 0
x 2 ≥ 0
x 1^ 2 + x 2 ^2 ≥ 1
x 1^ 2 + x 2 ^2 ≤ 2
با یک تابع هدف به حداکثر رساندن
f ( x ) = x 1 + x 2
که در آن( x = ( x 1 ، x 2 .
مثال 3 بعدی [ ویرایش ]
خطی از سطح بالا با فضای محدود در مرکز نشان دهنده راه حل است.
یک مشکل ساده دیگر (see diagram) را می توان با محدودیت ها تعریف کرد
x 1 ^2 - x 2 ^2 + x 3 ^2 ≤ 2
x 1 ^2 + x 2 ^2 + x 3^ 2 ≤ 10
با یک تابع هدف به حداکثر رساندن
f ( x ) = x 1 x 2 + x 2 x 3
که در آن( x = ( x 1 ، x 2 ، x 3 .
همچنین نگاه کنید به [ ویرایش ]
- منحنی انعطاف پذیر
- حداقل مربعات به حداقل رساندن
- برنامه ریزی خطی
- nl (فرمت)
- حداقل مربعات غیر خطی
- فهرست نرم افزار بهینه سازی
- برنامه ریزی درجه دوم محدود به طور محدود
- ورنر فنگل ، که پایه و اساس برنامه نویسی غیر خطی را ایجاد کرد
| پنهان کردناین مقاله دارای مسائل متعدد است. لطفا به بهبود آن کمک کنید یا درباره این مسائل در صفحه بحث بحث کنید . ( یاد بگیرید چگونه و هنگام حذف این پیام های قالب )
|
بهینه سازی محدب یک زیرمجموعه بهینه سازی ریاضی است که مسئله کاهش توابع محدب را بر مجموعه های محدب بررسی می کند . در حالی که بسیاری از کلاس های مشکلات بهینه سازی محدب، الگوریتم های چندجمله ای را پذیرفته اند، [1] بهینه سازی ریاضی به طور کلی NP-hard است . [2] [3] [4]
بهینه سازی محدب دارای کاربردهای زیادی در طیف گسترده ای از رشته ها مانند سیستم های کنترل اتوماتیک ، برآورد و پردازش سیگنال ، ارتباطات و شبکه ها، طراحی مدار الکترونیکی ، [5] تجزیه و تحلیل داده ها و مدل سازی، مالی ، آمار ( طراحی تجربی مطلوب ) [6] و بهینه سازی ساختاری . [7] با پیشرفت های اخیر در الگوریتم های محاسبات و بهینه سازی ، برنامه نویسی محدب تقریبا همانندبرنامه نویسی خطی است . [8]
فهرست
تعریف [ ویرایش ]
یک مشکل بهینه سازی محدب یک مشکل بهینه سازی است که در آن تابع هدف یک تابع محدب است و مجموعه ای از اجزای محدب است . تابع


![\ theta \ in [0،1]](https://wikimedia.org/api/rest_v1/media/math/render/svg/fead1e7dceab4be5ab2e91f5108144722daa8c36)




به طور خاص، مشکل بهینه سازی محدب مشکل یافتن برخی از آنها است 

کجا هدف تابع 




فرم استاندارد [ ویرایش ]
اگر به عنوان نوشته شده باشد، یک مشکل بهینه سازی محدب در فرم استاندارد قرار دارد
جایی که 







بسیاری از مشکلات بهینه سازی می توانند در فرم استاندارد مطابقت داده شوند. به عنوان مثال، مشکل حداکثر سازی یک تابع مقعر 

خواص [ ویرایش ]
ویژگی های مفید مفاهیم بهینه سازی محدب زیر: [13] [11]
- هر حداقل محلی یک حداقل جهانی است ؛
- مجموعه مطلوب محدب است
- اگر تابع هدف به شدت محدب باشد، مشکل بیشتر از یک نقطه مطلوب است.
این نتایج توسط تئوری کمینه شدن محدب همراه با مفاهیم هندسی از تجزیه و تحلیل عملکردی (در فضاهای هیلبرت) مانند نظریه طرح ریزی هیلبرت ، قضیه طرح تفکیکپذیری ، و لما فورکاس استفاده می شود .
مثالها [ ویرایش ]
کلاسهای مشکل زیر، تمام مشکلات بهینه سازی محدب هستند، یا می توانند از طریق تغییرات ساده به مشکلات بهینه سازی محدب از طریق تغییرات ساده کاهش یابند: [11] [14]
یک سلسله مراتب از مشکلات بهینه سازی محدب. (LP: برنامه خطی، QP: برنامه درجه دوم، برنامه مخروطی SOCP دوم، SDP: برنامه semidefinite، CP: برنامه مخروطی، GFP: برنامه فرم گراف.)
- کمترین مربعات
- برنامه ریزی خطی
- محدب به حداقل رساندن درجه دوم با محدودیت های خطی
- به حداقل رساندن درجه دوم با محدودیت های محدب محدب
- بهینه سازی مخروطی
- برنامه نویسی هندسی
- برنامه دوم مخروط سفارش
- برنامه نویسی نیمه تمام
- حداکثر شدن آنتروپی با محدودیت های مناسب
ضرایب لاگرانژ [ ویرایش ]
یک مشکل کمینه سازی محدب را با استفاده از یک تابع هزینه در فرم استاندارد مطرح کنید 



تابع Lagrangian برای این مشکل است
برای هر نقطه 




به حداقل می رساند
به طور کلی
با حداقل یکی
(کم خونی).
اگر یک نقطه "کاملا قابل اجرا" وجود داشته باشد، یعنی یک نقطه است
سپس بیانیه فوق می تواند تقویت شود تا این نیاز باشد 
برعکس، اگر برخی






الگوریتم ها [ ویرایش ]
مشکلات بهینه سازی محدب می تواند با روش های معاصر زیر حل شود: [15]
- روش های بسته بندی (وولف، لیماچال، کیویل)، و
- روش های پیش بینی متقارن ( Polyak )،
- روش های داخلی نقطه ای [16] ، که از توابع مانع نفس خود استفاده می کند [17] و توابع مانع از خودارضایی. [18]
- روش های برش هواپیما
- روش الی فساد
- روش متداول
- Subgradients دوگانه و روش رانش به جای جریمه
روش های متداول می توانند به سادگی اجرا شوند و به طور گسترده ای مورد استفاده قرار می گیرند. [19] روش های دوگانه گرافیکی، روش های زیرگروه ای است که برای یک مشکل دوگانه استفاده می شود . رانش به علاوه مجازات روش شبیه به Subgradient method برنامهریزی دو است، اما طول می کشد به طور متوسط هم از متغیرهای اولیه.
افزونه ها [ ویرایش ]
افزونه های بهینه سازی محدب شامل بهینه سازی توابع دوقطبی ، شبه محدب و توابع کواسیوکریم هستند. پسوند تئوری تحلیل محدب و روشهای تکراری برای تقریبا حل مشکلات کمینه سازی غیر غوطه وری در زمینه تخفیف تعمیم یافته ، همچنین به عنوان تحلیل محدب انتزاعی شناخته می شود.
همچنین نگاه کنید به [ ویرایش ]
| علم اقتصاد |
|---|
 نمودار عرضه و تقاضا، |
|
| علم اقتصاد |
|---|
اقتصاد خرد[نهفتن] تقاضا • عرضه و تقاضا • تولید •هزینه • نقدشوندگی • تورم • کالا •خدمات • پول • زیان • شکست بازار •گمرک • مزایده • دانش مالی •مالیات • بهرهوری • تجارت آزاد •ارزش افزوده • اقتصاد نفت •اقتصاد مهندسی • اقتصاد کشاورزی •اقتصاد محیط زیست |
دیگر اق |
اقتصاد خرد (به انگلیسی: Microeconomics) شاخهای از علم اقتصاد است که به مطالعه منحصر به فرد اقتصاد، تجزیه و تحلیل بازار، رفتار مصرفکنندگان و خانوارها و بنگاهها میپردازد و اساس آن مدلهای ریاضیاست. اقتصاد خرد چگونگی رفتار انسانها و انتخابهایشان را در سطح واحدهای خرد یا کوچک اقتصادی مانند یک فرد، یک بنگاه، یک صنعت یا بازار یک کالای خاص بررسی میکند و به چگونگی تعامل بین خریداران و مصرفکنندگان و عوامل مؤثر در انتخاب خریداران میپردازد. اقتصاد خرد بهخصوص به الگوی عرضه و تقاضا برای کالاها و خدمات و همچنین تعیین قیمت خروجی در بازارهای خاص توجه دارد و معمولاً در بازارهایی که در آن کالاها در حال خرید و فروش هستند کاربرد دارد.
محتویات
- ۱تفاوت بین اقتصاد خرد و کلان
- ۲تعاریف اولیه
- ۳اهداف اقتصاد خرد
- ۴زمینههای مهم در علم اقتصاد خرد
- ۵قانون تقاضا و عرضه
- ۶جستارهای وابسته
- ۷پانویس
- ۸منابع
- ۹پیوند به بیرون
تفاوت بین اقتصاد خرد و کلان[ویرایش]
اقتصاد خرد یا اقتصاد میکرو راجع به رفتارهای گروههای انفرادی است، حال آنکه اقتصاد کلان یا ماکرو، رفتارهای اقتصادی در سطح کلی را مورد بررسی قرار میدهد. اقتصاد خرد، مباحثی چون رفتار مصرفکننده، رفتار تولیدکننده و چگونگی تعیین قیمت در بازارهای مختلف را دربر میگیرد. حال آنکه اقتصاد کلان، تغییرات متغیرهای اقتصادی از قبیل درآمد ملی، سطح اشتغال و سطح عمومی قیمتها را مورد مطالعه و تحلیل قرار میدهد.[۱]
تعاریف اولیه[ویرایش]
- کالای مکمل و کالای جانشین: کالاهای مکمل کالاهایی هستند که به موازات یکدیگر مورد تقاضا واقع میشوند، مثل اتومبیل و لاستیک اتومبیل. کالاهای جانشین به آن دسته از کالاها اطلاق میشود که بتوانند جانشین یکدیگر شوند مثل فندک به جای کبریت.[۲]
- کالای مادی و کالای غیرمادی: کالاها بر دو نوع هستند: یا مادی اند (مثل نان و کره و اتومبیل) یا غیرمادی اند یعنی خدماتی هستند (مثل خدمات مشاورهای، خدمات بانکی و بیمه).[۳]
اهداف اقتصاد خرد[ویرایش]
یکی از اهداف اقتصاد خرد بررسی بازار و برقرار کردن یک رابطهٔ نسبی پولی بین کالاها و خدمات است. همچنین به بررسی موارد شکست بازار (مواردی که بازار قادر به تولید نتیجهٔ مطلوب و درخور نبوده) میپردازد و تئوریهایی را برای داشتن یک بازار رقابتی شرح میدهد.
در نظریه عرضه و تقاضا معمولاً فرض بر این قرار داده میشود که فضا کاملاً رقابتی است. این بدین معناست که خریداران و فروشندگان بسیاری در بازار وجود دارند و هیچکدام از آنها نمیتوانند بر قیمتها تأثیر بگذارند. در معادلات زندگی واقعی این فرض با مشکل مواجه است زیرا بسیاری از خریداران و فروشندگان این توانایی را دارند که بر قیمتها تأثیرگذار باشند. در خصوص نظریهٔ عرضه و تقاضا در اغلب موارد تجزیه و تحلیل پیچیدهای نیاز است تا بتوان یک مدل عرضه و تقاضا ارائه داد.
زمینههای مهم در علم اقتصاد خرد[ویرایش]
اقتصاد خرد خود به سه بخش تقسیم میشود: برقراری تعادل عمومی، انتخاب تحت عدم اطمینان، تئوری بازیها و در نظر گرفتن کشش عرضه و تقاضا درون سیستم بازار.
قانون تقاضا و عرضه[ویرایش]
آلفرد مارشال، اقتصاد دان برجسته انگلیسی
بازار رقابتی کامل، بازاری است که در آن تعداد زیادی فروشنده، کالاهای مشابه را به تعداد زیادی از خریداران، عرضه میکنند. قیمت در بازار به وسیله عرضه و تقاضا تعیین میشود. آلفرد مارشال، عرضه و تقاضا را به دو لبه قیچی تشبیه میکند که برای بریدن پارچه لازم است. او معتقد است که عرضه و تقاضا مانند دو تیغ قیچی، به یکدیگر کمک کرده، قیمت کالاها در بازار را تعیین میکنند. عرضه منعکسکننده شرایط کمیابی و تقاضا بیانکننده خواستهها و نیاز افراد میباشد. اگر کالایی کمیاب باشد ولی کسی تمایلی برای خرید آن نداشته باشد، واضح است که آن کالا نمیتواند قیمتی داشته باشد.[۴]
مطلوبیت
از ویکیپدیا، دانشنامهٔ آزاد
واژه مطلوبیت (به انگلیسی: Utility) به معنای فایده و سودمندی است[۱] که در فارسی اکثراً به «مطلوبیت» ترجمه میشود؛ اگرچه این ترجمه از نظر معنا نادرست است؛ اما چون دو واژه فایده و سودمندی در متون اقتصادی در معنای دیگری کاربرد دارند، بهتر است از همان واژه مطلوبیت به جای Utility استفاده شود.[۲]
محتویات
- ۱تعریف اصطلاحی مطلوبیت در اقتصاد
- ۲کاربردها
- ۳ترجیحات آشکار شده
- ۴سیر تعاریف مطلوبیت از زمان جرمی بنتام تا به امروز
- ۵توابع مطلوبیت
- ۶مطلوبیت انتظاری
- ۷مطلوبیت غیرمستقیم
- ۸نقد و بررسی
- ۹مفهوم مطلوبیت کل و نهایی
- ۱۰جستارهای وابسته
- ۱۱منابع
تعریف اصطلاحی مطلوبیت در اقتصاد[ویرایش]
به تعریف اقتصاددانان مطلوبیت کیفیتی است که کالایی را برای افراد خواستنی میکند.[۳] به بیان دیگر، مطلوبیت عبارت است از رضایت مصرفکننده که ازمصرف کالا و خدمات (در واقع هرآنچه نیازها و خواستههای انسان را ارضا میکند) حاصل میشود.[۴] در واقع کلمهٔ کلیدی مطلوبیت رضایت است نه سودمندی.[۵]
این مفهوم زیربنای اصل انتخاب عقلانی در اقتصاد و نظریه بازیها است. اقتصاددانان از آن جایی که میزان رضایت و خوشحالی حاصل از مصرف کالا و خدمات غیرقابل اندازهگیری است، روشهایی را برای اندازهگیری و نشان دادن مطلوبیت ابداع کردهاند. اقتصاددانان سعی کردهاند روشهای انتزاعی مقایسه مطلوبیت را از طریق مشاهده و محاسبه انتخابهای اقتصادی تکمیل کنند. به بیان ساده، اقتصاددانان مطلوبیت را تمایل مردم به پرداخت مبالغ مختلف برای کالاهای مختلف میدانند.
مفهوم مطلوبیت بسیار وسیع است و مترادف لذت شخصی میباشد. برای نمونه مصرف مواد مخدر برای افراد مضر میباشد ولی برای یک معتادی که به آن حس نیاز میکند لذتبخش میباشد، در نتیجه فرد معتاد به لحاظ بالا بردن لذت یا فرار از درد در کوتاه مدت از آن استفاده میکند و این کالا برای او اصطلاحاً دارای مطلوبیت یا خوشایندی میباشد.
در هنگام گزینش کالاها و خدمات مسلماً کالایی را برخواهیم گزید که برای ما مطلوبیت بیشتری داشته باشد. تمایل مردم معمولاً بر این است که از بابت مقدار پولی که برای یک کالا یا خدمت میپردازند مطلوبیتی به دست آورند که بیشتر از مطلوبیت خود آن پول باشد یا این که از زحمت (عدم مطلوبیت) ناشی از کار برای کسب آن میزان پول بیشتر باشد.
کاربردها[ویرایش]
معمولاً مطلوبیت توسط اقتصاددانان در ساختارهایی مانند منحنی بیتفاوتی بکارگرفته میشود. منحنی بیتفاوتی، نشاندهنده ترکیبی از کالاها و خدماتی است که مصرف آنها موجب دریافت میزان مشخصی از رضایت برای فرد یا جامعه میشود. اقتصاددانان از مطلوبیت و منحنیهای بیتفاوتی به عنوان زیربنایی برای فهم نمودار تقاضا، که نیمی از تحلیلهای عرضه و تقاضای بکار رفته برای تحلیل کارکرد بازار کالا را فراهم میکند، استفاده میکنند.
مطلوبیت فردی و اجتماعی میتواند به ترتیب به عنوان ارزش تابع مطلوبیت و تابع رفاه اجتماعی تفسیر شود. همانطور که در منحنیهای قرارداد توسط جعبهٔ اجورث مصور میشود، زمانی که این دو با قیود تولید و کالا تلفیق شوند، تحت برخی شرایط، این توابع میتوانند برای تحلیل کارایی پارتویی استفاده شوند. این کارایی مفهوم اصلی اقتصاد رفاه است. در مالیه، مطلوبیت برای ایجاد قیمت منحصری برای دارایی به نام قیمت بیتفاوتی بکار کرفته میشود. توابع مطلوبیت همچنین به اندازهگیری ریسک مربوط هستند.
ترجیحات آشکار شده[ویرایش]
اقتصاددانان پی بردهاند که مطلوبیت به صورت مستقیم غیرقابل مشاهده و محاسبه است و در عوض، راهی برای استنباط مطلوبیت نسبی اصلی از انتخابات مشاهده شده ابداع کردهاند. این موارد توسط سامیلسون «ترجیحات آشکار شده» نامگذاری شده و بهطور مثال در تمایل به پرداخت مردم آشکار شدند:
مطلوبیت وابسته به امیال و خواستهها در نظر گرفته میشود. امیال نمیتوانند به صورت مستقیم محاسبه شوند، بلکه تنها به صورت غیرمستقیم توسط پدیدههای ظاهری ای که موجبشان میشوند، محاسبه میشوند و در موارد دخالت عمده اقتصاد، توسط قیمتی که فرد تمایل به پرداخت آن برای ارضای خواسته اش دارد، اندازهگیری میشود.[۶]
سیر تعاریف مطلوبیت از زمان جرمی بنتام تا به امروز[ویرایش]
واژهٔ مطلوبیت را اولین بار پروفسور جرمی بنتام انگلیسی مطرح کرد. اصل کلی فلسفه بنتام بر منفعتگرایی و مطلوبیت استوار است. معاصرین بنتام از واژهٔ مطلوبیت در مباحث حقوقی، سیاسی، اجتماعی و اقتصادی استفاده میکردند اما به تعریف مشخصی از این واژه دست نیافته بودند. در این زمان بنتام برای اولین بار به تعریف دقیق این اصطلاح پرداخت. او در کتاب «مقدمهای بر اصول اخلاقیات و قانونگذاری» دربارهٔ رفتار انسانی چنین نوشت: «طبیعت، انسان را تحت سلطه دو خداوندگار مقتدر قرار دادهاست: لذت و رنج». وی سپس اصل مطلوبیت را به عنوان اصلی اخلاقی معرفی نموده و عنوان میکند که حداکثر شدن خالص لذت (یا لذت کل منهای مجموع درد و رنج)، تعیین میکند که عمل درست و صواب کدام است. این مبانی به این معناست که مطلوبیت قابل اندازهگیری است. بنتام معتقد بود هر کس با در نظر گرفتن هفت بعد اصلی لذت، که به آنها اشاره کرده بود، مطلوبیت خود را اندازهگیری کند و در ادامه به چهارده لذت ساده، دوازده رنج ساده، و عوامل مؤثر بر آنها اشاره میکند.[۷]
با این حال نه او و نه اقتصاددانان هم عصر او به درک رابطهٔ بین ارزش کالا و مطلوبیتی که از مصرف کالا به دست میآید نرسیدند. آدام اسمیت، رابطهٔ بین ارزش استفادهای و ارزش مبادلهای کالا را درک کرد تناقض مشهور آب و الماس را مطرح کرد. دیوید ریکاردو و کارل مارکس ارزش کالا را به میزان کاری که برای تولید آن به کار میرود مرتبط کردند.[۸] امیلکودر، از نمایندگان تجدیدنظر طلبی در تاریخ اندیشه اقتصادی، مدعی است که آدام اسمیت و ریکاردو که تحتتاثیرپروتستانیسم بودند، با تأکید بر نظریه صرفاً انگلیسی- پروتستانی ارزش- کار، موجب به تأخیر افتادن پذیرش نظریه ارزش مبتنی بر مطلوبیت شدند.[۹] استانلی جونز کسی بود که به رابطهٔ بین قیمت و مطلوبیت اشاره کرد. جونز به نقش کلیدی مطلوبیت در اقتصاد اشاره میکند و اعتقاد دارد که ارزش، تماماً بستگی به مطلوبیت دارد و علم اقتصاد باید بر مبنای مطلوبیّت ریخته شود. او همچنین مطلوبیت را امری نسبی و تابع شرایط گوناگون و در ارتباط با کالاها و خدمان مختلف میدانست.[۱۰]
دربرداشت کلاسیکی و نئوکلاسیکی در مورد مطلوبیت تفاوتی وجود دارد. کلاسیکها مطلوبیت را به عنوان خصیصهٔ عمومی یک کالا محسوب میکنند و نقش مطلوبیت و تقاضا در قیمت یک کالا را نادیده گرفته بودند. در حالی که اقتصاد دانان نئوکلاسیکی بر این باورند که مطلوبیت نه یک اندیشهٔ مطلق، بلکه رابطهٔ نسبی بین شیء و انسان است. آلفرد مارشال به تبیین این مسئله پرداخت. او با وارد کردن تحلیلهای هندسی در اقتصاد توانست سیستم بینابینی را ارائه کند که تلفیقی است از تئوری " کار ارزش" ریکاردو و تئوری " مطلوبیت ارزش " نئوکلاسیکها.[۱۱]
اما امروزه مطلوبیت در معنای مدرن آن حاوی هیچ اطلاع خاصی از "سطح لذت " ناشی از مصرف یک چیز نیست بلکه حتی نمیتوان رابطهٔ علت و معلولی بین مطلوبیت و انتخاب افراد را در نظر گرفت. در واقع مطلوبیت چیزی نیست مگر یک مفهوم جعلی که کار ما را در مدلسازی رفتار انسانی راحتتر میکند.[۱۲]
توابع مطلوبیت[ویرایش]
بر سر این مسئله امکان محاسبه مطلوبیت کالا کمی جدال وجود داشتهاست. در یک زمان، فرض میشد که مصرفکننده میتواند مطلوبیت حاصل از مصرف کالا را به صورت دقیق بیان کند. اقتصاددانانی که این فرض را داشتند، از دسته اقتصاددانان کاردینال بودند. امروزه توابع مطلوبیت، که میزان مطلوبیت را به ازای مصرف مقادیر مختلف کالا بیان میکنند، به دو دسته اردینال و کاردینال تقسیمبندی میشوند. این تقسیمبندی بر این اساس است که آیا آنها اطلاعاتی بیش از صرفاً تقسیمبندی کالاها بر اساس الویت و ترجیحات بیان میکنند یا خیر.
مطلوبیت کاردینالی[ویرایش]
اقتصاد دانان مانند ویلیام استانلی جونز و آلفرد مارشال در جواب این سؤال که آیا میتوان مطلوبیت را اندازهگیری کرد اینطور استدلال میکردند که مطلوبیت قابل اندازهگیری است و میتوان مطلوبیت را به وسیلهٔ واحدی به نام (یوتیل) اندازهگیری عددی کرد.[۱۳] این افراد معتقدند که مطلوبیت نه تنها قابل اندازهگیری است بلکه جمع پذیر نیز هست، به این معنی که میتوان مطلوبیت به دست آمده از مصرف دو کالا را با یکدیگر جمع کرد. اقتصاد دانان مانند اجورث و فیشر با نظریه عددی بودن مطلوبیت مخالف بودند؛ و این عقیده را داشتند که مطلوبیت کسب شده ناشی از مصرف یک کالا در یک مکان در مقابل مصرف یک کالای دیگر در مکان دیگر اندازهگیری میشود. از نظر این افراد اگرچه مطلوبیت قابل اندازهگیری است، اما جمع پذیر نیست و باید به مقدار مصرف همزمان کالاها برای اندازهگیری توجه کرد.[۱۴] نظریه ارزش کار که ریشه در عقاید فلسفی هلنی (یونان باستان) داشت به این مفهوم ارتباط پیدا میکند.
زمانی که اهمیت تفاوت مطلوبیت به عنوان کمیتی با اهمیت زیاد از نظر اخلاقی یا رفتاری در نظر گرفته شود، از مطلوبیت کاردینالی استفاده میشود. برای مثال، فرض کنید که مطلوبیت یک لیوان آب پرتغال ۱۲۰ واحد (یوتیل)، مطلوبیت یک فنجان چای ۸۰ یوتیل و مطلوبیت یک لیوان آب ۴۰ یوتیل است. با استفاده از مطلوبیت کاردینالی نتیجهگیری میشود که یک لیوان آب پرتغال، همان قدر که یک فنجان چای از یک لیوان آب بهتر است، از یک فنجان چای بهتر است. اما نمیتوانیم این نتیجهگیری را کنیم که خوبی یک فنجان چای دو سوم یک لیوان آب پرتغال است زیرا این نتیجهگیری نه تنها وابسته به اهمیت تفاوت مطلوبیت است، بلکه وابسته به «صفر» مطلوبیت نیز هست. برای مثال، اگر «صفر» مطلوبیت در نقطهٔ ۴۰- باشد، آنگاه یک لیوان آب پرتغال ۱۶۰ یوتیل بیش از صفر و یک فنجان چای ۱۲۰ یوتیل بیش از صفر است.
اقتصاد نئوکلاسیک به جد از استفاده از توابع مطلوبیت کاردینالی به عنوان اساس رفتار اقتصادی خودداری کردهاست. استثنا قابل توجه این موضوع، تحلیل انتخاب تحت شرایط ریسک است. گاهی از مطلوبیت کاردینالی برای جمعآوری مطلوبیت افراد و ایجاد تابع رفاه اجتماعی استفاده میشود. .
مطلوبیت اردینالی[ویرایش]
بعدها اقتصاد دانان دیگر نظریه متفاوتی ارائه دادند که اول اینکه مطلوبیت افراد را نمیتوان اندازهگیری کرد و دوم مطلوبیت غیرقابل اندازهگیری را میتوان رتبهبندی کرد. مثلاً مصرف ناشی از کالای X بیشتر یا کمتر یا مساوی کالای Y است؛ ولی نمیتوان گفت که از مصرف کالای x، یا کالای y، چند عدد (مثلاً ۳۰۰ یا ۴۰۰)یوتیل مطلوبیت به دست میآید.[۱۳])پاره تو اولین کسی بود که با کنار گذاشتن مطلوبیت کاردینالی، تئوری رفتار مصرفکننده را بر اساس مطلوبیت اردینالی مطرح کرد.[۱۵]
به عنوان نمونه میتوان گفت که مطلوبیت این سبد کالایی بیشتر یا کمتر یا مساوی سبد کالایی دیگر است. لازم است ذکر شود که یک سبد کالایی هم میتواند شامل کالاها باشد هم شامل خدمات. کالاها و خدمات هردو بخشی از کالاهای اقتصادی هستند.
زمانی که یوتیلها (ارزشهای تابع مطلوبیت) اهمیتی از نظر اخلاقی یا رفتاری ندارند و بیمعنی هستند، از مطلوبیت کاردینالی استفاده میشود. شاخص مطلوبیت، یک ترتیب رفتاری میان اعضای مجموعهٔ انتخابی رمزگذاری میکند، اما اطلاعاتی راجع به «قدرت ترجیحات» در اختیار قرار نمیدهد. در مثال فوق، تنها چیزی که واضح است این است که آب میوه به چای و چای به آب ترجیح دارد. توابع مطلوبیت اردینال تا تغییرات افزایشی یکنوا منحصر به فرد هستند. برای مثال، اگر تابع 



ترجیحات[ویرایش]
با اینکه طبق قرارداد، ترجیحات پایه اقتصاد خرد هستند، اغلب نمایش ترجیحات و تحلیل غیرمستقیم رفتار انسان با استفاده از تابع مطلوبیت ساده است. فرض کنید x مجموعه مصرف باشد؛ مجموعهای از تمام سبدهای منحصر به فردی از کالا که مصرفکننده امکان مصرف آنها را دارد.
تابع مطلوبیت مصرفکننده 

معمولاً در مدلهای اقتصاد خرد، یک مجموعهٔ محدود از L کالا وجود دارد و مصرفکننده میتواند به میزان دلخواه از هر کالا مصرف کند. مجموعهٔ مصرف 








ترجیحات آشکارشده در مالیه[ویرایش]
در کاربردهای مالی مانند بهینهسازی سبد سرمایهگذاری، یک سرمایهگذار سبد سرمایهگذاری ای را انتخاب میکند که تابع مطلوبیتش را حداکثر یا به همان نسبت معیار ریسک را حداقل کند. برای مثال، نظریه سبد سرمایهگذاری جدید واریانس را به عنوان معیار ریسک در نظر میگیرد. نظریههای متداول دیگر، نظریه چشمانداز[۱۶] و نظریه مطلوبیت انتظاری[۱۷] هستند. میتوان برای تعیین تابع مطلوبیت خاص هر سرمایهگذار، روند پرسشنامهای طراحی کرد: مثلاً شما برایx% احتمال دریافت y چه مقدار حاضر به پرداخت هستید؟ نظریه رجحان آشکار شده یک روش میان بر پیشنهاد میکند. سبد سرمایهگذاری X* ای که سرمایهگذار در حال حاضر در دست دارد را در نظر میگیرد و سپس تابع مطلوبیت یا معیار اندازهگیری را به گونهای تعیین میکند که X*سبد سرمایهگذاری بهینه شود.[۱۸]
مثالها[ویرایش]
برای سادهسازی محاسبات، فروض متعدد دیگری در رابطه با جزئیات ترجیحات انسان ساخته شدهاند، که شامل توابع مطلوبیت زیر میشوند:
- CES (کشش جانشینی ثابت)
- مطلوبیت هم کشش
- مطلوبیت نمایی
- مطلوبیت شبه خطی
- تابع مطلوبیت استون-گیری
- فرم دوقطبی گورمن:
- ترجیحات گرینوود-هرکویتز-هافمن
- ترجیحات کینگ-پلوسر-ربلو
- ریسک گریزی مطلق شبه هذلولی
اکثر توابع مطلوبیت مورد استفاده در مدلسازی و نظریات منظم هستند. آنها معمولاً یکنوا و شبه مقعر هستند. اما، امکان اینکه ترجیحات با استفاده از توابع مطلوبیت قابل نمایش نباشند وجود دارد. برای مثال، ترجیحات فرهنگ نگاشتی مداوم نیستند و امکان نشان دادن آنها با یک تابع مطلوبیت مداوم وجود ندارد.[۱۹]
مطلوبیت انتظاری[ویرایش]
تئوری مطلوبیت انتظاری مربوط به تجزیه و تحلیل انتخابات میان پروژههای ریسکی با چندین پیامد است. تناقض سن پترزبورگ اولین بار توسط نیکولاس برنولی در سال ۱۷۱۳عنوان شد و توسط دنیل برنولی در سال ۱۷۳۸ حل شد. دنیل برنولی استدلال میکند که اگر تصمیم گیرندگان از خود رفتار ریسک گریزانه نشان دهند، این پارادوکس حل میشود و یک تابع مطلوبیت کاردینال لگاریتمی در نظر میگیرد.
اولین کاربرد مهم تابع مطلوبیت انتظاری، استفاده جان وان نیومن و اسکار مورگنسترن از فرض حداکثرسازی مطلوبیت انتظاری در نظریه بازی هاست.
تئوری مطلوبیت وان نیومن-مورگنسترن[ویرایش]
وان نیومن و مورگنسترن موقعیتهایی را عنوان کردند که پیامدهای انتخابها به یقیین مشخص نیست اما پیامدها احتمالهایی را به همراه خود دارند. یک نمادگذاری برای قرعه کشی اینگونه است: اگر A وB هرکدام احتمال p و ۱ − p را در قرعه کشی داشته باشند، رابطهٔ خطی اینگونه است:
به صورت کلی، برای یک قرعه کشی با چندین بازیکن داریم: 
وان نیومن و مورگنسترن با استفاده از برخی فروض عقلایی مرتبط با رفتار تصمیمگیری نشان دادند که اگر یک فرد نماینده بتواند میان بخت آزماییها انتخاب کند، آنگاه آن فرد نماینده تابع مطلوبیتی دارد که در آن مطلوبیت یک بخت آزمایی دلخواه میتواند از طریق ترکیب خطی مطلوبیتها، با وزون برابر احتمال وقوع محاسبه شود.
این تئوری، تئوری مطلوبیت انتظاری نام دارد. فروض لازم، چهار اصل بدیهی در مورد خواص رابطه ترجیحات فرد بر بخت آزماییهای ساده (بخت آزماییهایی با ۲ بازیکن) هستند. {\displaystyle B\preceq A}
- تمامیت: برای هر دو بخت آزمایی ساده
و
، یا
یا
است یا هر دو (که در آن صورت هر دو به یک میزان مطلوبند)
- تعدی: برای هر سه بخت آزمایی
، اگر
و
باشد آنگاه
است.
- تحدب: اگر
باشد، آنگاه احتمال
بین ۰ و ۱ وجود دارد که بخت آزمایی
به اندازهٔ
مطلوب باشد.
- استقلال: برای هر سه بخت آزمایی {\d
،le L\preceq
است اگر و تنها اگر
باشد.
تنها زمانی 




اصل بدیهی ۳ و ۴ به ما اجازهٔ تصمیمگیری راجع به مطلوبیت نسبی دو بخت آزمایی یا دو دارایی را میدهد.
به عبارت دیگر، تابع مطلوبیت وان نیومن- مورگنسترن یک تابعی است که به انتخابات، اعداد واقعی نسبت میدهد: 




در میان تمام بدیهیات، استقلال از همه بیشتر طرد شدهاست. انواع مختلفی از تئوریهای مطلوبیت انتظاری کلی عنوان شدهاند، که اکثر آنها فرض چهارم را مد نظر قرار نمیدهند.
احتمال موفقیت[ویرایش]
کستگنولی و لیکالزی و بردلی و لیکالزی(۲۰۰۰) تفسیر دیگری از تئوری وان نیومن و مورگنسترن عنوان کردند. برای هر تابع مطلوبیت، یک قرعهٔ مرجع فرضی مخصوص با مطلوبیت انتظاری یک بخت آزمایی دلخواه که برابر احتمال عملکرد بهتر یا برابر قرعهٔ مرجع است وجود دارد. فرض کنید که موفقیت به عنوان پیامد بهتر یا همانند پیامد قرعهٔ مرجع باشد. آنگاه این تساوی ریاضی به این معناست که حداکثرسازی مطلوبیت انتظاری برابر حداکثرسازی احتمال موفقیت است. در بسیاری از زمینهها، این موجب تسهیل توجیه و اعمال مفهوم مطلوبیت میشود. برای مثال، مطلوبیت یک بنگاه ممکن است احتمال برآوردن انتظارات نامشخص خریداران باشد.[۲۰][۲۱][۲۲][۲۳]
مطلوبیت غیرمستقیم[ویرایش]
یک تابع مطلوبیت غیرمستقیم، ارزش بهینه دستیافتنی یک تابع مطلوبیت داده شدهای را میرساند که وابسته به قیمت کالاها، درآمد یا سطح ثروتی است که فرد دارا میباشد.
پول[ویرایش]
یکی از کاربردهای مفهوم مطلوبیت غیرمستقیم، مفهوم مطلوبیت پول است. تابع مطلوبیت غیرمستقیم پول یک تابع غیرخطی ای است که کراندار و نامتقارن است. تابع مطلوبیت در ناحیه مثبت مقعر است و بازتابی از پدیدهٔ نزولی بودن مطلوبیت نهایی است. کراندار بودن تابع نشاندهندهٔ این است که از نقطهای به بعد، پول دیگر سودمند نیست زیرا اندازهٔ هر اقتصاد در هر نقطهای از زمان خود محدود است. نامتقارن بودن تابع بازتابی از این واقعیت است که از دست دادن و بدست آوردن پول پیامدهای اساساً متفاوتی را برای افراد و کسب و کارها دارد. غیرخطی بودن تابع مطلوبیت پول پیامدهای ژرفی در فرایند تصمیمگیری دارد: در مواقعی که نتایج تصمیمات از طریق بدست آوردن و از دست دادن پول، که در اکثر محیطهای کسب و کار معمول است، بر مطلوبیت تأثیر بگذارد، انتخاب بهینه برای تصمیم معیین وابسته به نتایج ممکن تصمیمات دیگر در همان دورهٔ زمانی است.[۲۴]
نقد و بررسی[ویرایش]
ژوئن رابینسون انتقاد مشهوری دارد که مطلوبیت را مفهومی مدور عنوان میکند: «مطلوبیت مقدار کالایی است که افراد تمایل به خریدش را دارند و اینکه افراد تمایل به خرید کالاها دارند نشاندهندهٔ مطلوبیت است»[۲۵]:۴۸ رابینسون همچنین اشاره میکند که اینکه این تئوری فرض میکند ترجیحات ثابت هستند نشان میدهد که مطلوبین یک فرض آزمونپذیر نیست. این به این دلیل است که اگر تغییری در رفتار افراد در رابطه با تغییر در قیمتها یا تغییر در بودجه ایجاد شود، ما نمیتوانیم اطمینان داشته باشیم که این تغییر در رفتار تا چه حدی ناشی از تغییرات قیمت و بودجه و تا چه حدی ناشی از تغییرات در ترجیحات است.[۲۶] این انتقاد مشابه انتقاد فیلسوف هنس البرت است که ادعا میکند که فرض ثبات سایر شرایطی که پایه تئوری تقاضای نهایی است، خود یک حشو قبیح است و کاملاً غیرقابل آزمایش است.[۲۷] در اصل، منحنی عرضه و تقاضا (که مسیر نظری مقداری از کالا است که به ازای هر قیمتی، عرضه و تقاضا را نشان میدهد) صرفاً وابسته به هستیشناسی است و هیچگاه نمیتواند به صورت تجربی نشان داده شود.
انتقاد دیگر این ادعا است که مطلوبیت کاردینال و اردینال هیچیک در دنیا واقعی به صورت تجربی قابل مشاهده نیستند. در مورد مطلوبیت کاردینال، غیرممکن است که سطح رضایتمندی زمانی که شخصی کالایی را مصرف یا خریداری میکند، به صورت مقداری اندازهگیری شود. در مورد مطلوبیت اردینال، غیرممکن است که تصمیمگیریهای فرد هنگام خریداری کالایی تعیین شود. هر عمل شامل ترجیحات بر روی مجموعهٔ وسیعی از انتخابها خواهد بود (مانند سیب، آب پرتغال، سبزیجات دیگر، قرصهای ویتامین C، ورزش، عدم خرید و غیره)[۲۸][۲۹]
پاسخ سئوالات دیگر راجع به اینکه استدلالها برای ورود به تابع مطلوبیت به چه چیزی نیاز دارند دشوار است اما به نظر میرسد که برای فهم مطلوبیت ضروری است. اینکه مردم از ارتباط خواستهها، اعتقادات یا احساس وظیفه مطلوبیت کسب کنند یا نه کلید فهم رفتار آنها در ارغنون مطلوبیت است.[۳۰] به صورت مشابه، انتخاب میان جایگزینها، خود یک پروسه تعیین موارد در نظر گرفته شده به عنوان جایگزین و مسئلهٔ تصمیمگیری در نااطمینانی است.[۳۱]
مفهوم مطلوبیت کل و نهایی[ویرایش]
به مطلوبیت حاصل از کل کالاهای مصرف شده مطلوبیت کل (Utility Total) میگویند. هر قدر واحدهایی از یک کالا که مورد مصرف فرد در واحد زمان قرار میگیرد بیشتر باشد، مطلوبیت کلی که بدست میآید نیز بیشتر است.[۳۲]
مطلوبیت نهایی (اضافی)(Marginal Utility) عبارت از تغییر در مطلوبیت کل به ازاء تغییر یک واحد از مقدار کالای مصرف شده در یک دورهٔ زمانی مشخص است.[۱۳]
مطلوبیت نهایی
از ویکیپدیا، دانشنامهٔ آزاد
در نمودار مطلوبیت نهایی شیب ابتدا مثبت است. با افزایش مقدار (پایین نمودار)، شیب کاهش میابد تا جاییکه صفر شده و سپس منفی میگردد.
مطلوبیت نهایی اصطلاحی در علم اقتصاد است که به تغییرات مطلوبیت کل، حاصل از بدست آوردن مصرف یک یا چند واحد بیشتر از کالا یا خدمات اشاره دارد. مطلوبیت حاشیهای، شیب منحنی مطلوبیت کل است. تا زمانی که مطلوبیت حاشیهای مثبت باشد، مطلوبیت کل با ادامهٔ مصرف افزایش مییابد، اما در صورت منفی شدن مطلوبیت حاشیهای، مطلوبیت کل هم کم میشود. در جایی که مطلوبیت کل بیشترین مقدار خود را دارد، مطلوبیت حاشیهای صفر است.[۱] مطلوبیت حاشیهای را میتوان به صورت «تغییرات درمطلوبیت بر اثر مصرف یک واحد بیشتر از کالا» نیز تعریف کرد.
قانون کاهش مطلوبیت حاشیهای که توسط آلفرد مارشال (۱۸۴۲–۱۹۲۴ میلادی) ارائه شده، بیان میکند که برای هر فرد مطلوبیت حاشیهای هر چیزی با هر بار افزایش در میزان مصرفش، کاهش پیدا میکند. برای نمونه فردی که در طول یک بازهٔ زمانی یک هفتهای، یک بستنی میخورد، مقداری احساس رضایت (مطلوبیت) میکند، با خوردن بستنی دوم در همان هفته، میزان رضایتِ کل افزایش مییابد، اما میزان افزایش رضایت بر اثر خوردن بستنی دوم، احتمالاً کمتر از میزان افزایش رضایت بر اثر خودن بستنی اول خواهد بود و در دفعات بعدی نیز این روند ادامه مییابد.[۲]
مطلوبیت حاشیهای از واژه انگلیسی (marginal utility) گرفته شدهاست. مطلوبیت حاشیهای کالایی مانند X عبارت است از تغییر در مطلوبیت نهایی (کل) در ازای یک واحد اضافی کالای X در هر واحد زمان. واژه مطلوبیت اولین بار به وسیله پروفسور جرمی بنتام انگلیسی مطرح شد. در هر حال نه وی و نه اقتصاددانان هم عصر وی رابطه بین ارزش کالا و مطلوبیتی که از مصرف کالا حاصل میشود را درک نکردهاند.[۳]
محتویات
- ۱شرط تعادل مصرفکننده (قانون برابری مطلوبیتهای نهایی)
- ۲نظریهٔ کاردینالی مطلوبیت نهایی
- ۳قانون نزولی بودن مطلوبیت نهایی
- ۴تابع مطلوبیت نهایی برگسون-ساموئلسون
- ۵مطلوبیت نهایی و استخراج منحنیهای بیتفاوتی
- ۶جستارهای وابسته
- ۷منابع
شرط تعادل مصرفکننده (قانون برابری مطلوبیتهای نهایی)[ویرایش]
آدام اسمیت رابطه بین ارزش استفادهای و ارزش مبادلهای کالا را تشخیص داد و مثال معروفش را در مورد الماس و آب بیان کرد. بدین ترتیب که الماس، قیمت (ارزش مبادله ای) بالایی دارد. اما ارزش آن برای زندگی کم است. یعنی ارزش استفادهای کمی دارد. این در حالی است که آب قیمت (ارزش مبادله ای) کمی دارد اما برای زندگی بسیار ضروری است یعنی ارزش استفادهای بسیار بالایی دارد. تنها ویلیام استنلی جونز بود که به رابطه بین مطلوبیت و قیمت اشاره کرد. او استدلال نمود که این مطلوبیت نهایی (و نه مطلوبیت کل) است که به قیمت مرتبط میشود. وی در کتابش (تئوری اقتصاد سیاسی) مطلوبیت نهایی را به صورت سیستماتیک بسط داده وباتوجه به مثال آب و الماس میتوان نتایج وی را به صورت زیر نوشت:[۳]
(آب-مطلوبیت نهایی)/(آب-قیمت)=(الماس-مطلوبیت نهایی)/(الماس-قیمت)
این رابطه نشان میدهد که بین مطلوبیت آخرین واحد پولی که برای خرید آب و مطلوبیت آخرین واحد پولی که برای خرید الماس تخصیص دادهاست برابری بر قرار است. ما میتوانیم قانون برابری مطلوبیتهای نهایی را نه تنها در مورد دو شیء بلکه در مورد مجموعهای از کالاها که مصرفکننده در لحظهٔ معینی میتواند درآمد خود را تقسیم کند تعمیم دهیم.[۴]
MU_1/P_1 =MU_2/P_2 =⋯=〖MU〗_n/P_n
بنابراین تعادل مصرفکننده به وضعیتی اطلاق میشود که یک فرد، درآمد خود را به قسمتی برای خرید کالاهای متفاوت تقسیم کند که بیشترین ارضاء و مطلوبیت را بدست آورد.[۵]
نظریهٔ کاردینالی مطلوبیت نهایی[ویرایش]
تئوری کاردینالی مطلوبیت حاکی از آن است که مطلوبیت هم درست مثل قیمت قابل اندازهگیری است به این معنی که میتوانیم مقدار مطلوبیت هر کالا را تعیین کنیم. برای مثال مصرف یک سیب ۲۰ یوتیل مطلوبیت دارد. در نظریهٔ کاردینالی مطلوبیت هم مطلوبیت کل وهم مطلوبیت نهایی قابل اندازهگیری است.[۳]گوسن که نظریه مطلوبیت ابتدا توسط وی مطرح شد معتقد بود که نه تنها مطلوبیت کل بلکه مطلوبیت نهایی نیز به واسطه اعداد قابل اندازهگیری میباشند.[۶]
قانون نزولی بودن مطلوبیت نهایی[ویرایش]
گوسن در قانون اول خود میگوید " مطلوبیت نهایی یک کالا با افزایش مصرف آن و با عدم تغییر مصرف کالاهای دیگر کاهش پیدا میکند. این قانون را " قانون نزولی بودن مطلوبیت نهایی " یا " قانون سیری " مینامیم. لازم است که یادآور شویم که ممکن است اندازهٔ مصرف برخی از کالاها ابتدا باعث افزایش مطلوبیت نهایی شود (مثل فرد تشنهای که جرعهٔ اول آب را مینوشد) ولی بعد از آنکه مصرف آن از حدی گذشت مطلوبیت نهایی کاهش پیدا میکند و قانون نزولی بودن به قوت خود باقی خواهد ماند.[۶]
فردی به مصرف سیب میپردازد و برای هر سطح معلوم مصرف از این کالا، او بیشتر را به کمتر برای کالای دیگر ترجیح میدهد. حال اگر فرد از مصرف یک سیب ۱۰۰ واحد مطلوبیت کسب نماید و از طرفی از مصرف دو سیب ۱۷۰ واحد مطلوبیت به دست آورد مطلوبیت نهایی او از مصرف دومین سیب ۷۰ واحد است. اگر فرد میزان سیب مصرفی خود را افزایش دهد و در مجموع سه سیب مصرف کند کل مطلوبیت حاصل از مصرف میوهها مثلاً ۲۰۰ واحد است و مصرف سیب سوم برای او ۳۰ واحد مطلوبیت ایجاد کردهاست به ترتیب با افزایش مصرف سیب مطلوبیت نهایی کاهش میابد و این به معنای نزولی بودن مطلوبیت نهایی است.[۳]
تابع و منحنی مطلوبیت نهایی
نمودار مطلوبیت نهایی را از روی نمودار مطلوبیت کل میتوان استخراج نمود. زمانی که مطلوبیت کل حداکثر میشود مطلوبیت نهایی صفر خواهد شد و از این به بعد با مصرف بیشتر مطلوبیت کل کاهش و مطلوبیت نهایی منفی میشود.[۷]
اگر تغییرات مقدار مصرف کالای Xزیاد باشد از روش خطی استفاده میکنیم:
MUᵪ =∆U/∆X اگر تغییرات X کوچک باشد به مشتقگیری از تابع مطلوبیت کل میپردازیم: MUᵪ =lim∆U/∆X=du/dx مطلوبیت نهایی شیب منحنی مطلوبیت کل است بنابراین تا هنگامی که شیب منحنی مطلوبیت نهایی مثبت است مطلوبیت کل در حال افزایش است اشباع هنگامی رخ میدهد که مطلوبیت کل به حداکثر مقدار خود رسیده باشد که در این نقطه مطلوبیت نهایی صفر است.[۶]
تابع مطلوبیت نهایی برگسون-ساموئلسون[ویرایش]
وزنهای رفاهی به این معنی هستند که بر اثر افزایش مصرف یا درآمد افراد مطلوبیت آنها افزایش مییابد. این افزایش مطلوبیت را مطلوبیت نهایی مصرف یا درآمد میگوییم. در جامعه این تغییرات بر اثر اجرای یک برنامه یا طرح رخ خواهد داد. اگر اجرای طرح منجر به افزایش یکسان درآمد افراد فقیر و غنی شود به علت متفاوت بودن مطلوبیت نهایی درآمد دوگروه رفاهشان به یک میزان تغییر خواهد کرد و شایان ذکر است که مطلوبیت جامعه از افزایش مطلوبیت افراد فقیر بیشتر از افراد غنی افزایش پیدا میکند (چون مطلوبیت نهایی گروه فقیر بیشتر از مطلوبیت نهایی گروه غنی است). لذا مطابق نظر اسچرینر (۱۹۸۹،schreiner) به منظور رسیدن به حداکثر رفاه بر اثر اجرای یک پروژه اجتماعی بایستی هزینهها و منافع آن طرح براساس مطلوبیت نهایی درآمد بین افراد توزیع شود یعنی به افراد فقیر درمقایسه با افراد غنی وزن بیشتری داده شود چرا که مطلوبیت نهایی درآمد نزولی است. پس میتوان مناطق یک کشور را که از نظر مصرف (درآمد) سرانه متفاوت هستند تقسیمبندی کرد و وزنهای مختلفی را بر اساس مطلوبیت نهاییشان نسبت داد. برای این کار باید از تابع رفاه اجتماعی استفاده شود که معمولاً آن را از نوع تابع مطلوبیت نهایی برگسون-ساموئلسون در نظر میگیرند.[۸]
مطلوبیت نهایی و استخراج منحنیهای بیتفاوتی[ویرایش]
به دلیل وجود نقاط ضعف در نظریه مصرفکننده بر اساس مطلوبیت، نظریهٔ دیگری طرح و ارائه گردید که به نام منحنیهای بیتفاوتی مشهور است. در این تحلیل به جای اندازهگیری مطلوبیت با اعداد از مطلوبیت رتبهبندی شدهاستفاده میشود، بدین ترتیب که اگر نتوانیم بگوییم فلان کالا ۳ یا ۴ درجه (یاواحد) مطلوبیت ایجاد میکند، میتوانیم بگوییم که فلان کالا یا مجموعه کالا، مطلوبیتی کمتر ویا بیشتر از کالا یا مجموعه کالای دیگر به دست میدهد. براساس این نظریه فرد ویا خانوار میتواند مجموعهای از مقادیر مختلف دو کالای تقریباً قابل جانشین که مطلوبیت یکسانی را به بار میآورد،انتخاب کند.[۹]
هزینه کل
از ویکیپدیا، دانشنامهٔ آزاد
تجزیه مجموع هزینه ها به عنوان مجموعهزینه های ثابت و هزینه های متغیر. در هزینه-حجم-سود تجزیه و تحلیل
منحنی کل هزینهها غیر خطی میتواند نشان دهنده افزایش و کاهش بازده باشد.
در اقتصاد و حسابداری هزینه کل (TC) توصیف کل هزینه اقتصادی تولید و ساخته شده است به عبارت دیگر مجموع هزینههای متغیر و هزینه های ثابت هستند که مستقل از کمیت خوبی تولید شده و شامل ورودی (سرمایه) است.
دیگر مدل های اقتصادی باید کل متغیر منحنی هزینه (و در نتیجه کل هزینه منحنی) نشان دادن مفاهیم افزایش و بعد کاهش های حاشیه ای را برمی گرداند.
در بازاریابی لازم است بدانید که چگونه کل هزینه های شکاف میان متغیر و ثابت شده است. "این تمایز بسیار مهم، در پیش بینی درآمد تولید شده توسط تغییرات مختلف در واحد فروش و در نتیجه تاثیر مالی از پیشنهاد کمپین های بازاریابی است." در یک نظرسنجی از حدود 200 مدیران ارشد بازاریابی 60 درصد پاسخ دادند که آنها "متغیر و هزینه های ثابت" متریک بسیار مفید است.[۱]
همچنین نگاه کنید[ویرایش]
- نیمه متغیر هزینه
- منحنی هزینه
- کل هزینه خرید
- کل هزینه مالکیت
منابع[ویرایش]
- ↑ Farris, Paul W.; Neil T. Bendle; Phillip E. Pfeifer; David J. Reibstein (2010).
- متوسط کل هزینه
(ATC) = کل هزینه / Q (خروجی مقدار تولید یا 'Q')
- متوسط هزینه متغیر
(AVC) = کل هزینه متغیر / ...
- متوسط هزینه های ثابت
(AFC) = ATC – AVC
- هزینه کل
(TC) = (AVC + AFC) X خروجی (که Q)
- کل هزینه متغیر
(TVC) = AVC X خروجی
- مجموع هزینه های ثابت
(TFC) = TC – TVC
- هزینه نهایی
(MC) = تغییر در هزینه کل / تغییر در خروجی
- محصول نهایی
(MP) = تغییر در کل محصول / تغییر در متغیر عامل
- درآمد نهایی
(MR) = تغییر در درآمد کل / تغییر در ...
- میانگین محصول
(AP) = TP / متغیر عامل
- درآمد کل
(TR) = قیمت X مقدار
- میانگین درآمد
(AR) = TR / خروجی
- کل محصول
(TP) = AP متغیر X Factor
- اقتصادی سود
= TR – TC> 0
- از دست دادن
= TR – TC <0
- شکستن حتی نقطه
= AR = ATC
- به حداکثر رساندن سود
Condition = MR = MC
از ویکیپدیا، دانشنامه آزاد
در اقتصاد ، منحنی هزینه یک نمودار هزینه های تولید به عنوان عملکرد کلی تولید می باشد. در یک اقتصاد بازار آزاد ، شرکت های تولید کننده موثر، فرآیند تولید خود را با به حداقل رساندن هزینه های سازگار با هر سطح ممکن از تولید، بهینه می کنند و نتیجه منحنی هزینه است؛ و شرکت های به حداکثر رساندن سود استفاده از منحنی هزینه برای تصمیم گیری مقدار خروجی. انواع مختلفی از منحنی های هزینه وجود دارد که همه مربوط به یکدیگر هستند، از جمله منحنی هزینه کل و متوسط؛ حاشیه ای ("برای هر واحد اضافی") منحنی هزینه، که برابر با تفاوت از منحنی هزینه کل؛ و منحنی هزینه متغیر بعضی از آنها قابل اجرا هستندکوتاه مدت ، دیگران در درازمدت .
فهرست
- 1نماد
- 2کل هزینه های کوتاه مدت (SRTC) و منحنی کل هزینه های طولانی (LRTC)
- 3متغیر کوتاه مدت و منحنی هزینه ثابت (SRVC و SRFC یا VC و FC)
- 4میانگین منحنی هزینه متغیر کوتاه مدت (SRAVC)
- 5منحنی هزینه ثابت منحصرا کوتاه مدت (SRAFC)
- 6منحنی های کل هزینه های کوتاه مدت و بلند مدت (SRATC یا SRAC و LRATC یا LRAC)
- 7منحنی هزینه های نقدینگی کوتاه مدت (SRMC)
- 8منحنی هزینه های حاشیه ای طولانی مدت (LRMC)
- 9نمودار منحنی هزینه همراه با منحنی درآمد
- 10منحنی هزینه و توابع تولید
- 11رابطه بین منحنی های مختلف
- 12رابطه بین منحنی های هزینه کوتاه مدت و بلند مدت
- 13منحنی U شکل
- 14شکل تجربی منحنی هزینه متوسط
- 15همچنین ببینید
- 16یادداشت
- 17منابع
نماد [ ویرایش ]
اختصارات استاندارد برای هر مفهوم هزینه وجود دارد، بیان شده در شرایط مختلف از توصیف های زیر:
- SR = کوتاه مدت (زمانی که مقدار سرمایه فیزیکی را نمی توان تنظیم کرد)
- LR = طولانی مدت (زمانی که تمام مقدار ورودی را می توان تنظیم کرد)
- A = متوسط (در واحد خروجی)
- M = حاشیه ای (برای یک واحد اضافی خروجی)
- F = ثابت (غیر قابل تنظیم)
- V = متغیر (قابل تنظیم)
- T = کل (متغیر ثابت ثابت)
- C = هزینه
اینها را می توان به روش های مختلف برای بیان مفاهیم مرتبط با هزینه های مختلف (با SR و LR اغلب زمانی که زمینه روشن است حذف شده است): یکی از گروه اول (SR یا LR)؛ هیچ یک از گروه دوم (A، M یا هیچ (به معنی "سطح")؛ از گروه سوم (F، V، یا T) و ماده چهارم (C). از این موارد، ما به طور خاص SRTC و LRTC؛ SRAC (یا SRATC) و LRAC (یا LRATC)؛ SRMC و LRMC؛ و تنها در SR تنها VC، FC و AVC.
منحنی های کل هزینه کوتاه (SRTC) و هزینه های طولانی مدت (LRTC) [ ویرایش ]
منحنی کل هزینه، اگر غیر خطی باشد، می تواند نمایانگر افزایش و کاهش بازده های حاشیه ای باشد.
منحنی های کل هزینه های کوتاه مدت و بلند مدت در میزان تولید تولید افزایش می یابند، زیرا تولید خروجی بیشتر نیاز به استفاده بیشتر از نیروی کار در هر دو کوتاه مدت و طولانی مدت دارد و به این دلیل که در بلندمدت تولید تولید بیشتر شامل استفاده از بیشتر از ورودی سرمایه فیزیکی؛ و استفاده از هر یک از این ورودی ها شامل افزایش هزینه های ورودی می شود.
با در نظر گرفتن تنها یک متغیر ورودی (استفاده از نیروی کار) در کوتاه مدت، هر مقدار ممکن از خروجی نیاز به مقدار خاصی از استفاده از کار، و هزینه کل کوتاه مدت به عنوان عملکرد از سطح خروجی این مقدار منحصر به فرد از کار است بار هزینه واحد کار اما در بلندمدت با مقادیر سرمایه و نیروی فیزیکی که بتواند انتخاب شود، کل هزینه تولید یک سطح خروجی خاص، نتیجه یک مشکل بهینه سازی است: مجموع هزینه های کار (میزان حقوق و دستمزد نسبت به انتخاب میزان استفاده از نیروی کار) و هزینه های سرمایه (هزینه واحد سرمایه به میزان انتخاب شده از میزان استفاده از سرمایه فیزیکی) با توجه به استفاده از نیروی کار و استفاده از سرمایه، با توجه به عملکرد تولید برابری مربوط به هر کدام از کاربردهای ورودی، کاهش می یابد؛
متغیر کوتاه مدت و منحنی هزینه ثابت (SRVC و SRFC یا VC و FC) [ ویرایش ]
هزینه های کل را می توان به عنوان مجموع هزینه های ثابت و هزینه های متغیر تجزیه کرد . در اینجا خروجی در امتداد محور افقی اندازه گیری می شود. درمدل تحلیل هزینه-سود-سود ، هزینه های کل به صورت خطی در حجم هستند.
از آنجایی که هزینه ثابت کوتاه مدت با سطح خروجی متفاوت نیست، منحنی آن افقی است که در اینجا نشان داده شده است. هزینه های متغیر با سطح خروجی افزایش می یابد، از آنجایی که خروجی بیشتر تولید می شود، بیشتر از ورودی متغیر (ها) باید مورد استفاده قرار گیرد و پرداخت شود.
منحنی متغیر هزینه متغیر کوتاه مدت (SRAVC) [ ویرایش ]
منحنی میانگین هزینه کوتاه (AC) U شکل. AVC میانگین هزینه متغیر، AFC میانگین هزینه ثابت و MC منحنی هزینه حاشیه حداقل حداقل منحنی میانگین منحنی هزینه متغیر و منحنی میانگین هزینه است.
میانگین هزینه متغیر (که یک مفهوم کوتاه مدت است) هزینه متغیر (معمولا هزینه کار) در واحد خروجی است: SRAVC = wL / Q که w نرخ دستمزد است، L مقدار کار استفاده شده است، و Q مقدار تولید تولید شده. منحنی SRAVC مقادیر متغیر کوتاه مدت کوتاه مدت را در برابر سطح خروجی قرار می دهد و به طور معمول به صورت U شکل شکل می گیرد. با این حال، در حالی که این امر برای نظریه اقتصادی مناسب است، بحث شده است که ارتباط کمی با دنیای واقعی دارد. برخی برآوردها نشان می دهند که حداقل برای تولید، نسبت شرکت هایی که یک منحنی هزینه ی U شکل را در اختیار دارند، در محدوده 5 تا 11 درصد قرار دارد. [1] [2]
منحنی هزینه ثابت منحصرا کوتاه (SRAFC) [ ویرایش ]
از آنجا که هزینه ثابت با تعریف با خروجی متفاوت نیست، میانگین آن در واحد خروجی پایین تر از زمانی است که خروجی بالاتر است، و منحنی منحنی پایین تری را نشان می دهد.
منحنی های کل هزینه های کوتاه مدت و بلند مدت (SRATC یا SRAC و LRATC یا LRAC) [ ویرایش ]
میانگین منحنی هزینه کل برای ایجاد رابطه بین هزینه ی واحد ی خروجی و سطح خروجی ، ceteris paribus ساخته شده است . یک شرکت کاملا رقابتی و کارآمد تولید کننده عوامل سازندهخود را سازماندهی می کند به طوری که استفاده از عوامل تولید به همان اندازه که ممکن است مطابق با سطح داده شده خروجی تولید شود. در کوتاه مدت ، زمانی که حداقل یک عامل تولید ثابت شده است، این اتفاق در سطح خروجی رخ می دهد که از آن به دست آورده شده است که از هرگونه افزایش احتمالی هزینه های بالقوه از افزایش تولید لذت می برد. این در نقطه حداقل در نمودار بالا است.
کل هزینه های کوتاه مدت توسط

جایی که P K قیمت واحد استفاده از سرمایه فیزیکی در واحد زمان است، P L قیمت واحد کار در واحد زمان (نرخ دستمزد)، K مقدار مقدار استفاده از سرمایه فیزیکی، و L مقدار کار استفاده می شود. از این طریق، هزینه متوسط کوتاه مدت را به دست می آوریم که SATC یا SAC را به عنوان STC / Q نشان می دهد.
SRATC یا SRAC = P K K / Q + P L L / Q = P K / AP K + P L / AP L ،
AP K = Q / K محصول متوسط سرمایه است و AP L = Q / L محصول متوسط کار است. [3] : 191
در نمودار بالا، منحنی میانگین میانگین هزینه و میانگین منحنی هزینه متغیر با صفر آغاز نمی شود، زیرا در مقدار صفر این مقادیر تعریف نمی شوند، زیرا آنها تقسیم صفر را شامل می شوند.
میانگین هزینه کوتاه مدت برابر با هزینه های ثابت ثابت به همراه میانگین هزینه های متغیر است. به طور متوسط هزینه ثابت به طور مداوم به عنوان افزایش تولید در کوتاه مدت کاهش می یابد، زیرا K در کوتاه مدت ثابت شده است. شکل میانگین منحنی هزینه متغیر به طور مستقیم با افزایش و سپس کاهش بازده های حاشیه ای به ورودی متغیر (به طور معمول کار) تعیین می شود. [4] : 210
منحنی متوسط هزینه های بلند مدت به نظر می رسد مشابه منحنی کوتاه مدت است، اما این اجازه می دهد که استفاده از سرمایه فیزیکی متفاوت باشد.
منحنی هزینه منحنی کوتاه (SRMC) [ ویرایش ]
منحنی هزینه معمولی منحصر به فرد
هزینه ی حاشیه ای کوتاه مدتمنحنی گرافیکی نشان دهنده رابطه بین هزینه های حاشیه ای (یعنی افزایش) است که توسط یک شرکت در تولید کوتاه مدت یک کالا یا خدمات و مقدار تولید تولید شده است. این منحنی ساخته شده است برای گرفتن رابطه بین هزینه حاشیه و سطح خروجی، نگه داشتن متغیرهای دیگر، مانند تکنولوژی و قیمت منابع، ثابت است. منحنی هزینه حاشیه معمولا U شکل است. هزینه های حاشیه ای در مقادیر کم خروجی نسبتا بالا است؛ پس از آنکه تولید افزایش می یابد، هزینه های حاشیه ای کاهش می یابد، به حداقل می رسد و سپس افزایش می یابد. هزینه حاشیه در رابطه با درآمد حاشیه ای (MR)، مقدار افزایشی درآمد فروش که یک واحد اضافی از محصول یا سرویس به شرکت می آورد، نشان داده می شود. این شکل منحنی هزینه های حاشیه ای مستقیما به افزایش است،کاهش بازده های حاشیه ای ). هزینه مرزی برابر با w / MP L است .[3] : 191 برای اکثر فرآیندهای تولید، محصول حاشیه کار در ابتدا افزایش می یابد، به حداکثر مقدار می رسد و پس از آن به طور مداوم به عنوان افزایش تولید کاهش می یابد. بنابراین هزینه حاشیه ای ابتدا سقوط می کند، به حداقل مقدار می رسد و سپس افزایش می یابد. [4] : 209 منحنی هزینه های حاشیهای، هر دو میانگین منحنی هزینه متغیر و منحنی هزینه کل منفی (کوتاه مدت) را در حداقل امتیاز خود تقاطع می کنند. وقتی منحنی هزینه حاشیه بالاتر از منحنی هزینه متوسط باشد، منحنی متوسط رو به افزایش است. وقتی منحنی هزینه های حاشیه ای پایین تر از منحنی متوسط باشد، منحنی متوسط سقوط می کند. این رابطه صرف نظر از اینکه آیا منحنی حاشیه در حال افزایش است یا در حال سقوط است.[5] : 226
منحنی هزینه حاشیهای (LRMC) طولانی مدت [ ویرایش ]
منحنی هزینه های حاشیه ای طولانی مدت برای هر واحد خروجی هزینه کل اضافه شده در طولانی مدت را نشان می دهد، یعنی زمانی که همه عوامل تولید متغیر هستند، نشان می دهد. در غیر این صورت، LRMC حداقل افزایش هزینه کل در ارتباط با افزایش یک واحد خروجی است، زمانی که همه ورودی ها متغیر هستند. [6]
منحنی هزینه های حاشیه ای طولانی مدت، با بازدهی به مقیاس ، یک مفهوم طولانی مدت، به جای قانون کاهش بازده های حاشیه ای ، که یک مفهوم کوتاه مدت است، شکل می گیرد. منحنی هزینه های حاشیه ای طولانی مدت با توجه به انعطاف پذیری ورودی، نسبت به کوتاه مدت آن هماهنگ است. منحنی هزینه های حاشیه ای درازمدت، منحنی متوسط هزینه های طولانی مدت را در حداقل نقطه دوم، تقاطع می کند. [3] : 208 هنگامی که هزینه حاشیه بلند مدت پایین تر از هزینه های میانگین طولانی مدت است، هزینه های میانگین دراز مدت کاهش می یابد (به عنوان واحد های تولید اضافی در نظر گرفته می شود). [3] : 207زمانی که هزینه حاشیهای بلندمدت بالاتر از میانگین بلند مدت است، هزینه متوسط افزایش مییابد. هزینه حاشیه ای طولانی برابر با هزینه های حاشیه ای کوتاه مدت در حد متوسط تولید در حد متوسط است. LRMC شیب تابع هزینه کل LR است.
نمودار منحنی هزینه همراه با منحنی درآمد [ ویرایش ]
منحنی هزینه در رقابت کامل نسبت به درآمد حاشیه ای
منحنی های هزینه می تواند برای ارائه اطلاعات در مورد شرکت ها ترکیب شود. به عنوان مثال در این نمودار، شرکت ها در بازار کاملا رقابتیقرار دارند. در یک بازار کاملا رقابتی قیمتی که بنگاهها در دراز مدت با آن روبرو می شوند، قیمتی است که منحنی هزینه های حاشیه ای منحنی هزینه را کاهش می دهد، زیرا هر قیمت بالاتر یا پایین آن منجر به ورود یا خروج از صنعت می شود. رانندگی قیمت تعیین شده بازار به سطح که به سود صفر اقتصادی است .
منحنی هزینه و عملکرد تولید [ ویرایش ]
فرض بر این است که قیمت عوامل ثابت است، تابع تولید تمام هزینه ها را تعیین می کند. [4] منحنی هزینه متغیر قیمت مداوم قیمت ورودی متغیر زمانی است که کارکرد تولید کوتاه مدت معکوس یا منحنی کل محصول، و رفتار و خواص آن توسط عملکرد تولید تعیین می شود. [3] : 209 [nb 1]از آنجا که تابع تولید، تابع هزینه متغیر را تعیین می کند، لزوما شکل و ویژگی های منحنی هزینه های منحنی و منحنی های هزینه متوسط را تعیین می کند. [4]
اگر شرکت یک رقیب کامل در تمام بازارهای ورودی است و بنابراین قیمت هر واحد از تمام ورودی های آن تحت تاثیر قرار نمی گیرد که چه مقدار ورودی ها شرکت خریداری می کند، می توان نشان داد که در یک سطح خاص خروجی، شرکت دارای مقیاس اقتصادی است (به عنوان مثال، در منطقه شیب دار پایین منحنی هزینه متوسط دراز مدت فعالیت می کند) و اگر تنها در صورت افزایش بازدهی در مقیاس باشد. [7] [8] [9] به همین ترتیب، آن است که عدم مقیاس از مقیاس (در منطقه شیب دار در بلندمدت منحنی متوسط هزینه های طولانی مدت کار می کند) اگر و فقط اگر آن را کاهش می دهد بازگشت به مقیاس، و نه دارای اقتصاد و یا diseconomies از مقیاس اگر آن را به بازده ثابت به مقیاس . در این مورد، با رقابت کامل در بازار خروجی، تعادل بازار بلندمدت، شامل همه شرکتهایی است که در حداقل نقطه منحنی هزینه های بلندمدت خود (یعنی در مرز بین اقتصاد و فقدان مقیاس) قرار دارند.
اگر، با این حال، شرکت یک رقیب کامل در بازارهای ورودی نیست، سپس نتایج فوق تغییر می یابند. به عنوان مثال، اگر در برخی سطوح از سطوح خروجی به مقیاس افزایش مییابد، اما شرکت در یک یا چند بازار ورودی بسیار بزرگ است و افزایش خرید آن از یک ورودی، هزینههای ورودی به ازای هر واحد را افزایش میدهد، سپس شرکت میتواند داشته باشد عدم تعادل در مقیاس در آن سطح از سطوح خروجی. از سوی دیگر، اگر شرکت بتواند تخفیف های عمده ای از یک ورودی را دریافت کند، می تواند در مقادیری از سطوح خروجی از مقیاس مقیاس برخوردار باشد، حتی اگر میزان بازده تولید در آن محدوده خروجی کاهش می یابد.
رابطه بین منحنی های مختلف [ ویرایش ]
- هزینه کل = هزینه های ثابت (FC) + هزینه متغیر (VC) = میانگین هزینه کل (ATC) x تعداد (Q)
- هزینه مرزی (MC) = dC / dQ؛ MC برابر شیب تابع هزینه کل و تابع هزینه متغیر است
- میانگین هزینه کل (ATC) = هزینه کل / Q
- میانگین هزینه ثابت (AFC) = FC / Q
- میانگین متغیر هزینه (AVC) = VC / Q.
- ATC = AFC + AVC
- در سطح Q که در آن منحنی MC بالاتر از میانگین کل هزینه یا میانگین منحنی هزینه متغیر است، منحنی دوم افزایش می یابد. [10] : 212
- اگر MC زیر هزینه متوسط کل یا میانگین هزینه متغیر باشد، منحنی دوم در حال کاهش است.
- اگر MC برابر با میانگین کل هزینه باشد، متوسط هزینه کل در حداقل مقدار آن است.
- اگر MC برابر با میانگین متغیر هزینه باشد، متوسط هزینه متغیر در حداقل مقدار آن است.
رابطه منحنی های کوتاه مدت و بلند مدت هزینه ها [ ویرایش ]
برای هر مقدار خروجی، یک سطح حداقل سرمایه کم هزینه و یک منحنی هزینه متوسط منحصر به فرد کوتاه مدت مرتبط با تولید مقدار داده شده وجود دارد. [11] دستورالعمل های زیر فرض می کنند که شرکت از مقدار مطلوب سرمایه برای مقدار تولید استفاده می کند. اگر نه، منحنی SRAC "به طور کامل بالاتر از" LRAC قرار می گیرد و در هر نقطه منحنی نمی شود.
- هر منحنی STC می تواند فقط در یک نقطه منحنی LRTC باشد. منحنی STC نمی تواند منحنی LRTC متقاطع (متقاطع) شود. [4] : 230 [10] : 228-229 منحنی STC می تواند به طور کامل "منحنی" بالای منحنی LRTC بدون نقطه tangency قرار گیرد. [12] : 256
- یک منحنی STC منحنی LRTC را در سطح تولید درازمدت کم هزینه می کند. در نقطه ای از همبستگی LRTC = STC. در تمام سطوح دیگر تولید STC از LRTC تجاوز می کند. [13] : 292-299
- توابع میانگین توزیع عبارتند از تابع هزینه کل تقسیم بر سطح خروجی. بنابراین، منحنی SATC نیز منحنی LRATC در سطح پایین تر هزینه خروجی است. در نقطه تماس LRATC = SATC. در تمام سطوح تولید دیگر SATC> LRATC [13] : 292-299 در سمت چپ نقطه تنگستن شرکت از سرمایه بیش از حد استفاده می کند و هزینه های ثابت بسیار بالا است. به راستی نقطه ضعف، شرکت از سرمایه کمتری استفاده می کند و بازدهی کار کم می شود و هزینه ها افزایش می یابد. [14]
- شیب منحنی هزینه کل برابر با هزینه حاشیهای است. بنابراین، هنگامی که STC به LTC مماس است، SMC = LRMC.
- در بلندمدت هزینه کم کردن سطح خروجی LRTC = STC؛ LRATC = SATC و LRMC = SMC،. [13] : 292-299
- سطح پایین تولید با حداقل هزینه ممکن است از حداقل SATC متفاوت باشد. [10] : 229 [15] : 186
- با هزینه ثابت واحد ورودی ها، اگر تابع تولید ثابت به مقیاس بازگشت، در حداقل سطح منحنی SATC ما SATC = LRATC = SMC = LRMC. [13] : 292-299
- با هزینه های واحد ثابت هزینه های ورودی، اگر تابع تولید افزایش می یابد به مقیاس، حداقل منحنی SATC به سمت راست از نقطه تضاد بین LRAC و منحنی SATC است. [13] : 292-299جایی که LRTC = STC، LRATC = SATC و LRMC = SMC.
- با هزینه ثابت واحد ورودی و کاهش بازده، حداقل منحنی SATC به سمت چپ نقطه اتصال بین LRAC و SATC است ، [13] : 292-299 که در آن LRTC = STC، LRATC = SATC و LRMC = SMC.
- با هزینه ثابت ورودی واحد، شرکتی که در حال افزایش (کاهش) بازدهی به مقیاس است و با حداقل SAC تولید می کند، می تواند هزینه های متوسط را در بلندمدت با افزایش (کاهش) استفاده از ورودی ثابت کاهش دهد. [13] : 292-99 [15] : 186
- LRATC همیشه برابر یا کمتر از SATC است. [3] : 211
- اگر روند تولید بازدهی ثابت را در مقیاس نشان می دهد، حداقل SRAC برابر با حداقل هزینه میانگین میانگین طول عمر است. LRAC و SRAC با حداقل مقادیر مشترک آنها روبرو می شوند. بنابراین در زیر بازده ثابت به مقیاس SRMC = LRMC = LRAC = SRAC.
- اگر روند تولید در حال کاهش یا افزایش است، حداقل هزینه کوتاه مدت کوتاه مدت حداقل هزینه میانگین میانگین طول عمر را با هم مقایسه نمی کند. اگر افزایش بازده به مقیاس وجود داشته باشد، حداقل طول عمر در سطح پایین تر از خروجی از SRAC رخ خواهد داد. این به این دلیل است که مقیاس های اقتصادی وجود دارد که مورد بهره برداری قرار نگرفته اند، بنابراین در یک درازمدت، یک شرکت همیشه می تواند با یک کارخانه بزرگتر قیمت کمتری از حداقل هزینه های کوتاه مدت کوتاه را تولید کند. [16]
- با کاهش بازده، حداقل SRAC در سطح تولید پایین تر از حداقل LRAC اتفاق می افتد، زیرا شرکت می تواند به سادگی کاهش اندازه و یا عملیات آن را کاهش می دهد.
- حداقل SRAC زمانی اتفاق می افتد که شیب صفر باشد. [17] بنابراین نقاط خطی بین منحنی LRAC U شکل و حداقل منحنی SRAC تنها با آن بخش از منحنی LRAC نشان داده شده اند که مقادیر ثابت دارند. برای افزایش بازده به مقیاس، نقطه تماس بین LRAC و SRAC باید در سطح خروجی زیر سطح با حداقل منحنی SRAC رخ دهد.
منحنی U شکل [ ویرایش ]
هر دو منحنی SRAC و LRAC معمولا به صورت U-shaped بیان می شوند. [10] : 211؛ 226 [15] : 182؛ 187-188 با این حال، شکل های منحنی به دلیل عوامل مشابه نیست. برای منحنی کوتاه مدت، شیب پایینی به طور عمده به دلیل کاهش میانگین هزینه های ثابت است. [4] : 227 افزایش بازده به متغیر ورودی در سطوح پایین تولید نیز نقش مهمی دارد [18]، در حالی که شیب بالا به دلیل کاهش بازده های حاشیه ای به ورودی متغیر است. [4] : 227 با شکل منحنی دراز مدت شکل طبق تعریف، اقتصاد و معایب مقیاس را نشان می دهد. [15] : 186در سطوح پایین عملکرد توابع تولید دراز مدت به طور کلی افزایش بازده به مقیاس را نشان می دهد، که برای شرکت هایی که رقبای کامل در بازارهای ورودی هستند، به معنی آن است که هزینه میانگین دراز مدت کاهش می یابد؛ [4] : 227 شیب رو به بالا از عملکرد متوسط هزینه های طولانی در سطوح بالاتر خروجی به دلیل کاهش بازده به مقیاس در آن سطوح خروجی است. [4] : 227
شکل تجربی منحنی های هزینه متوسط [ ویرایش ]
شواهدی وجود دارد که نشان می دهد منحنی های متوسط هزینه به طور معمول U شکل نیستند. در نظرسنجی از Wilford J. Eiteman و Glenn E. Guthrie در سال 1952، مدیران 334 شرکت تعدادی از منحنی های هزینه های مختلف را نشان دادند و خواسته می شود که کدامیک از بهترین منحنی هزینه شرکت را نشان می دهد. 95٪ از مدیران پاسخ به این نظرسنجی، منحنی های هزینه را با هزینه های ثابت یا سقوط گزارش دادند. [1]
آلن بلینجر ، معاون پیشین انجمن اقتصاد آمریکا ، در سال 1998 همان نوع نظرسنجی را انجام داد که شامل 200 شرکت آمریکایی در نمونه ای بود که باید نماینده اقتصاد ایالات متحده در کل باشد. وی دریافت که حدود 40 درصد از شرکت ها هزینه های متغیر یا حاشیه ای را کاهش می دهند و 48.4 درصد هزینه ثابت و متغیر ثابت را نشان می دهند. [19]
از ویکیپدیا، دانشنامه آزاد
منحنی خطی خطی (MR) و منحنی درآمد متوسط (AR) برای یک شرکت که در رقابت کامل نیست
در اقتصاد خرد ، درآمد حاشیه ای (MR) درآمد اضافی است که با افزایش فروش محصول توسط یک واحد تولید می شود. [1] [2] [3] [4] [5]
در یک بازار کاملا رقابتی ، درآمد اضافی حاصل از فروش یک واحد اضافی از یک محصول برابر با قیمت است که شرکت قادر به پرداخت هزینه خرید از محصول است. [3] [6] این به این دلیل است که یک شرکت در یک بازار رقابتی همواره قیمت یکسان برای هر واحد فروش را بدون در نظر گرفتن تعداد واحدهای که بنگاه فروش می کند، از آنجایی که فروش بنگاه هرگز نمی تواند بر قیمت صنعت تاثیر بگذارد، دریافت می کند. [1] [3]
با این حال، انحصار فروش کل صنعت را تعیین می کند . [1] در نتیجه، باید قیمت تمام واحدهای فروخته شده برای افزایش فروش را با 1 واحد کاهش دهد. [1] [3] بنابراین، درآمد حاشیه ای همیشه پایین تر از قیمت شرکت است که می تواند برای واحد فروخته شده است، زیرا هر کاهش قیمت باعث کاهش درآمد واحد در هر خوب شرکت می فروشد. [1] [3] درآمد حاشیه ای (افزایش درآمد کل) قیمت شرکتی است که در واحد فروش اضافی فروخته می شود، درنتیجه کاهش درآمد از طریق کاهش قیمت تمام واحدهای دیگر که قبل از کاهش قیمت فروخته شده اند، کاهش یافته است.
سود شرکت هنگامی بیشتر خواهد شد که درآمد نهایی (MR) برابر با هزینه حاشیه ای (MC) باشد. اگر


فهرست
تعریف [ ویرایش ]
درآمد حاشیه ای برابر با نسبت تغییر درآمد برای برخی تغییر در مقدار فروخته شده به آن تغییر در مقدار فروخته شده است. این نیز می تواند به عنوان یک مشتق نماینده، زمانی که تغییر در مقدار فروخته شده خودسرانه کوچک است. تابع درآمد را تعریف کنید
جایی که Q خروجی است و P ( Q ) تابع تقاضای معکوس مشتریان است. با حاکمیت محصول ، درآمد حاشیه ای توسط آن تعریف می شود
جایی که نشانه اول یک مشتق نشان می دهد. برای یک شرکت با رقابت کامل، قیمت با مقدار فروخته شده تغییر نمی کند (


منحنی درآمد منفی [ ویرایش ]
منحنی درآمد حاشیه ای تحت تاثیر عوامل مشابه منحنی تقاضا - تغییر درآمد، تغییرات قیمت مکمل ها و جایگزین ها، تغییر در جمعیت ها و غیره. این عوامل می توانند منحنی MR را تغییر و چرخش دهند. [8]
رابطه درآمد حاشیه ای و کشش [ ویرایش ]
رابطه بین درآمد حاشیه و انعطاف تقاضا توسط مشتریان شرکت می تواند به شرح زیر باشد: [9]
جایی که R مجموع درآمد است، P ( Q ) معکوس از تابع تقاضا است، و e <0 الاستیسیته تقاضا است . اگر تقاضا ناپذیر باشد ( e > -1)، MR منفی خواهد بود، زیرا برای فروش واحد محدود (infinitesimal) شرکت باید قیمت فروش را پایین بیاورد تا درآمد بیشتری را نسبت به واحدهای قبلی داشته باشد در واحد افزایشی به دست آورد. اگر تقاضا الاستیک باشد ( e<-1) MR مثبت خواهد بود، زیرا واحد اضافی قیمت را تا حد زیادی کاهش نخواهد داد. اگر شرکت یک رقیب کامل است، به طوری که در بازار بسیار کوچک است که میزان تولید و فروش آن بر قیمت اثر نداشته باشد، و سپس الاستیک قیمت تقاضا بی نهایت منفی است، و درآمد حقیقی به سادگی برابر با (بازار تعیین شده ) قیمت.
درآمد حاشیه ای و قیمت گذاری نشانه گذاری [ ویرایش ]
به حداکثر رساندن سود لازم است که یک شرکت تولید کند که درآمد حاشیه ای برابر با هزینه های حاشیه ای است. مدیران شرکت بعید است که اطلاعات کامل در مورد عملکرد درآمد نهایی خود و یا هزینه های حاشیه ای خود داشته باشند. با این حال، شرایط به حداکثر رساندن سود را می توان در شکل "به آسانی قابل اجرا" بیان کرد:
MR = MC،
MR = P (1 + 1 / e)،
MC = P (1 + 1 / e)،
MC = P + P / E،
(P - MC) / P = -1 / e. [10]
نشانه گذاری تفاوت قیمت و هزینه های حاشیه ای است. فرمول بیان می دارد که نشانه گذاری به عنوان یک درصد از قیمت برابر با منفی (و در نتیجه ارزش مطلق) معکوس از انعطاف پذیری تقاضا است. [10]
(P-MC) / P = -1 / e شاخص Lerner پس از اقتصاددان Abba Lerner نامیده می شود . [11] شاخص Lerner اندازه گیری قدرت بازار است - توانایی یک شرکت برای اتخاذ یک قیمت که بیش از هزینه های حاشیه ای است. شاخص از صفر متغیر است (زمانی که تقاضا بی نهایت الاستیک (یک بازار کاملا رقابتی) به 1 (زمانی که تقاضا دارای ضریب کشش -1) است. هر چه مقدار شاخص به 1 نزدیکتر باشد، تفاوت بین قیمت و هزینه حاشیه ای بیشتر است. شاخص لرنر به این دلیل افزایش می یابد که تقاضا کمتر الاستیک باشد. [11]
در عوض، رابطه را می توان بیان کرد:
P = MC / (1 + 1 / e).
بنابراین، برای مثال، اگر e -2 و MC 5.00 باشد، قیمت 10.00 دلار است.
به عنوان مثال اگر یک شرکت می تواند 10 واحد را به قیمت 20 دلار هر یا 11 واحد با قیمت 19 دلار به فروش برساند، درآمد حاصله از واحد یازدهم (11 × 19) - (10 × 20) = 9 دلار است.
همچنین نگاه کنید به [ ویرایش ]
یادداشت ها [ ویرایش ]
^ پرش به بالاب ج د ه برادلی R. چیلر، "ملزومات اقتصاد"، نیویورک: مک هیل، شرکت، 1991.
^ ادوین منسفیلد، "نظریه میکرو اقتصاد و برنامه های کاربردی، نسخه 3"، نیویورک و لندن: WW نورتون و شرکت، 1979.
^ پرش به بالاب ج د ه راجر لیروی میلر، "متوسط اقتصاد خرد تئوری مسائل نرم افزار، ویرایش سوم"، نیویورک: مک هیل، وارز، 1982.
^ Tirole، Jean، "Theory of Industrial Organization"، کمبریج، ماساچوست: MIT Press، 1988.
^ جان سیاه، "فرهنگ لغت اقتصاد اکسفورد"، نیویورک: دانشگاه آکسفورد، 2003.
^ O'Sullivan & Sheffrin (2003)، p. 112
^ دیوید.، Prentice ،؛ 1962- Waschik، Robert G. (2010). اقتصاد مدیریتی: یک رویکرد استراتژیک . Routledge پ. 33. ISBN 9780415495172. OCLC 432989728 .
^ Landsburg، S قیمت 2002 p. 137
^ Perloff (2008) p. 364
هزینه نهایی
از ویکیپدیا، دانشنامهٔ آزاد
در اقتصاد هزینه نهایی (به انگلیسی:marginal cost) به میزان تغییرات هزینهٔ کل بر اثر افزایش تولید به اندازهٔ یک واحد گفته میشود. اگر بخواهیم به صورت دیفرانسیلی بیان کنیم، هزینهٔ نهایی برابر است با میزان تغییرات هزینهٔ کل بر اثر تغییر یک واحدی خروجی.[۱]
محتویات
- ۱تعریف هزینه نهایی
- ۲تابع هزینه نهایی
- ۳منحنی هزینه نهایی
- ۴رابطه هزینه نهایی (MC) و تولید نهایی نیروی کار (MPL)
- ۵مقیاس اقتصادی
- ۶منحنی عرضه دربازار
- ۷جستارهای وابسته
- ۸پانویس
- ۹منابع
تعریف هزینه نهایی[ویرایش]
هزینه نهایی(MC) عبارت است از تغییر در هزینه کل در ازای تغییر یک واحد اضافی تولید در هر واحد زمان.[۲]
در این هزینه، فقط هزینههای متغیّر دخالت دارند؛ بهعنوان مثال، تولید یا عدم تولید یک واحد اضافی محصول، تغییری در هزینههای ثابت ندارد. یعنی به ازای یک واحد تغییر در تولید هزینه ثابت تغییری نمیکند. اما برای تولید یک واحد اضافی کالا، باید مواد اولیه اضافی داشته باشیم؛ که این خود، موجب بالا رفتن هزینه متغیر میشود.[۳]
تابع هزینه نهایی[ویرایش]
بر اساس آنچه در بالا توضیح داده شد رابطه ریاضی هزینه نهایی به شکل زیر خواهد بود:
اگر تغییرات تولید نسبتاً زیاد باشد، در این صورت مقدار تقریبی هزینه نهایی برابر است با:[۴]
منحنی هزینه نهایی[ویرایش]
مکان هندسی شیب کلیه خطوطی است که در هر نقطه از منحنی هزینه کل (TC) (یا هزینه متغیّر (TVC)) بر منحنی TC (یاTVC) مماس میگردند. این منحنی نیز اصولاً U شکل است یعنی منحنی هزینه نهایی ابتدا کاهش یافته و بعد به حداقل خود میرسد، آنگاه شروع به افزایش مینماید. سطح تولیدی که هزینه نهایی کمترین مقدار خود را دارد، نقطه عطف منحنی هزینه کل میباشد و شیب منحنی هزینه کل در این نقطه حداقل است.[۵]
رابطه هزینه نهایی (MC) و تولید نهایی نیروی کار (MPL)[ویرایش]
هزینه تولید به هزینه نیروی کار، این نیروی کار یک بهروزی نهایی دارد میخواهید ببینید آخرین نفری که استخدام کردید چقدر برایش هزینه کردید یعنی W) MC هزینه آخرین محصول ماست یعنی آخرین میزی که ساخته شده چقدر برای ما هزینه داشته. MC در حقیقت هزینه آخرین واحد محصول است به عبارت دیگر میخواهیم بگوییم آخرین کالایی که تولید شدهاست چه هزینهای داشتهاست میدانیم که این کالا آخرین واحد محصول مربوط به آخرین نفری است که استخدام کردیم بهروزی نهایی آخرین نفر استخدامی (MPL) مقدار تولیدی است که این فرد تولید کردهاست کل هزینهای که بابت این فرد پرداخت شدهاست. دستمزد او میباشد اگر این فرد به اندازه (MPL) محصول تولید کرده باشد و مابازای او W را پرداخته باشیم هزینه نهایی تولید یعنی هزینه آخرین کالای تولید شده برابر است با.
با فرض آنکه تنها نهاده تولیدی نیروی کار (L) بوده و ارزش هر واحد نهاده (L) یعنی دستمزد برابر با (W) باشد تولید نهایی برابر خواهد بود با 
رابطه هزینه نهایی (MC)وتولید نهایی نیروی کار(MPL)برابر خواهد بود با[۶]
مقیاس اقتصادی[ویرایش]
مقیاس اقتصادی در بلند مدت اتفاق میافتد. بلند مدت بازه زمانی است که هزینه ثابت نداریم و تمام هزینهها متغیر هستندو تولید ممکن است تحت تأثیر مقیاس اقتصادی یا مقیاس غیر اقتصادی قرار بگیرد. مقیاس اقتصادی زمانی خواهیم داشت که هزینه نهایی بلند مدت کمتر از هزینه متوسط بلند مدت باشد بنابر هزینه متوسط نزولی خواهد بود و برعکس زمانی که هزینه نهایی بیشتر از هزینه متوسط بلند مدت باشد مقیاس غیر اقتصادی داریم و هزینه متوسط بلند مدت صعودی خواهد بود.[۷]
منحنی عرضه دربازار[ویرایش]
آن بخش از هزینه نهایی کوتاه مدت (SMC) که بالاتر از هزینه متغیر کوتاه مدت (AVC) است یا آن قسمت از هزینه نهایی بلند مدت (LMC) که بالاتر از هزینه کل بلند مدت (LAC) است منحنی عرضه بازار خواهد بود. بنابراین در بازار رقابتی شرکتها سطح تولید خود را براساس منحنی هزینه نهایی و خط قیمت تعیین میکنند. و اگر هزینه نهایی بالاتر از قیمت باشد شرکت تولید نمیکند چون برایش سودآور نیست. بنابراین تولید در جایی اتفاق میافتد که هزینه نهایی برابر با قیمت باشد.[۸] اما اگر ساختار بازار انحصاری باشد انحصار گردارای منحنی عرضه نخواهد بوددر واقع آنچه منحنی عرضه نشان میدهد این است که در مقابل هر سطح از قیمت یک مقدار از تولید وجود دارد که سود را به حداکثر میرساند. انحصار گر در جایی تولید میکند که هزینه نهایی برابر با درآمد نهایی شود.[۹]
جستارهای وابسته[ویرایش]
از ویکیپدیا، دانشنامه آزاد
نظریه اعداد متعارف ، شاخه ای از نظریه اعداد است که اعداد متعارف (اعداد که راه حل های معادله چند جمله ای با ضرایب عدد صحیح نیستند )، در هر دو روش کیفی و کمی بررسی می شود.
فهرست
ترانسدانت [ ویرایش ]
مقاله اصلی: شماره ترانسدادنت
قضیه اساسی جبر به ما می گوید که اگر ما یک غیر صفر چند جمله ای با ضرایب عدد صحیح پس از آن که چند جمله ای یک ریشه در دارند اعداد مختلط . بدین معنی است که برای هر چندجمله ای Pبا ضرایب عدد صحیح، یک عدد پیچیده α وجود دارد به طوری که P (α) = 0. نظریه متعارف مربوط به سوال متقابل است: با توجه به تعداد پیچیده α، یک چندجمله P با ضرایب عدد صحیحی وجود دارد که P (α) = 0 اگر چنین چند جملهای وجود نداشته باشد، این عدد به معنای متعالی است.
به طور کلی این نظریه به استقلال جبری اعداد مربوط می شود. مجموعه ای از اعداد {α 1 ، α 2 ، ...، α n } به صورت جبری مستقل در یک میدان K نامیده می شود، اگر هیچ چندجمله ای غیر صفرP در n متغیر با ضرایب K وجود ندارد به طوری که P (α 1 ، α 2 ، ...، α N ) = 0. بنابراین کار کردن اگر یک عدد داده شده متعالی است که واقعا یک مورد خاص از استقلال جبری که در آن N = 1 و زمینه K است درست منطقی .
یک مفهوم مرتبط این است که آیا یک عبارت فرم بسته بسته برای یک عدد وجود دارد، از نمایی و لگاریتم و همچنین عملیات جبری. تعاریف مختلفی از "فرم بسته" وجود دارد، و سوالاتی در مورد فرم بسته، اغلب می تواند به سوالاتی در مورد فراموشی محدود شود.
تاریخچه [ ویرایش ]
تقریب اعداد عقلانی: لیوویل به روت [ ویرایش ]
استفاده از اصطلاح متعالی برای اشاره به یک شی است که نمی تاریخ جبری به قرن هفدهم، که گوتفرید لایبنیتس ثابت کرد که تابع مثلثاتی بود نه تابع جبری . [1] سوال این است که آیا طبقات خاصی از اعداد میتوانند فراتر از تعاریف باشند، به 1748 میرسند [2] وقتی اولر ادعا کرد [3] که تعداد log a b برای اعداد عقلانی a و b به صورت جبری نیست ، b است که از فرم b نیست = a cبرای برخی از منطقی ج .
ادعای اولر تا قرن بیستم ثابت نشده است، اما تقریبا صد سال پس از ادعای وی، جوزف لیوویل موفق به اثبات وجود اعداد است که جبری نیستند، چیزی که تا آن زمان به درستی شناخته نشده بود. مقالات اصلی او در مورد این مسئله در دهه 1840، استدلال هایی را با استفاده از تقسیمات ادامه داد تا اعداد متعالی را ساختند. بعدها، در دهه 1850، او شرایط لازم را برای یک عدد به جبری داد و به همین ترتیب شرایط کافی برای یک عدد متعالی بود. [4] این معیار متعقب به اندازه کافی قوی نبود که لازم باشد، و در واقع نمیتواند تشخیص دهد که عدد eمتعالی است اما کار او کلاس بزرگتری از اعداد متعالی را فراهم کرد، که در حال حاضر به عنوان عدد لیوویل به افتخار او شناخته شده است .
معیار لیوویل اساسا گفت که اعداد جبری نمیتواند به خوبی با اعداد منطقی تقریبآور شود. بنابراین اگر یک عدد بتواند به خوبی با اعداد منطقی تقریب برسد، آن باید فراتر از حد متعال باشد. معنای دقیق "خیلی خوب تقریبی" در کار لیوویل مربوط به یک نماینده خاص است. او نشان داد که اگر α یک درجه جبری درجه d ≥ 2 و هر عدد بیشتر از صفر است، آن عبارت
تنها تعداد محدودی از عقلانی p / q راضی می شود . با استفاده از این به عنوان یک معیار برای تعالی، بی اهمیت نیست، زیرا باید بررسی کنید که آیا برای هر d ≥ 2 راه حل بی نهایت برای p / qوجود دارد .
در کار قرن بیستم با الکس Thue ، [5] کارل سایگل ، [6] و کلاوس رود[7] توان در کار لیوویل از کاهش د ε به د / 2 1 ε، و در نهایت، در سال 1955، به 2 ε. این نتیجه، به عنوان قضیه تو-سایگل-رود شناخته شده است ، ظاهرا بهترین ممکن است، زیرا اگر عدد 2 ε با فقط 2 جایگزین شود، نتیجه دیگر درست نیست. با این حال، سرگ لانگ پیش بینی پیشرفت نتیجه Roth؛ به ویژه او فرض کرد که q 2 ε در مخرج سمت راست می تواند به q 2 log ( q) 1 ε .
کار روث به طور موثری کار را که توسط لیوویل آغاز شد، پایان داد و قضیه او به ریاضیدانان اجازه داد تا اثبات فراوانی بسیاری از اعداد بیشتر، مانند ثابت Champernowne . با این وجود، قضیه هنوز به اندازه کافی قوی نیست که بتواند تمام اعداد متعالی را شناسایی کند، و بسیاری از ثابتهای معروف از جمله e و π یا در معنی فوق نمی دانند یا به خوبی قابل تقلیل هستند. [8]
توابع کمکی: هرمیت بکر [ ویرایش ]
خوشبختانه روشهای دیگر در قرن نوزدهم برای مقابله با خواص جبری e و در نتیجه π از طریق هوستر اویلر پیشگام شدند . این کار بر استفاده از عملکرد به اصطلاح کمکی متمرکز است . اینها توابعهستند که معمولا در نقاط مورد نظر در تعداد زیادی صفر هستند. در اینجا "بسیاری از صفر" ممکن است به معنی بسیاری از صفر متمایز، و یا به عنوان چند به عنوان یک صفر اما با بالا تعدد ، و یا حتی بسیاری از صفر همه، با تعدد بالا. چارلز هرمیت از توابع کمکی استفاده کرد که توابع و kx را برای هر عدد طبیعی k تقریبا به منظور اثبات تعالیالکترونیکی در سال 1873. [9] کار خود را بر ساخته شد فردیناند فون لیندپمن در 1880s [10] به منظور ثابت کند که E α متعالی برای اعداد غیر صفر جبری آلفا. به طور خاص این ثابت کرد که π فراتر از آن است که e π i جبری است و بنابراین منفی مسأله عتیقه در مورد این که آیا این امکان وجود دارد که مربع دایره باشد جواب داد . کارل وایرستراس کار خود را هنوز ادامه داد و در نهایت قضیه لیندنمان و ویرشترس را در سال 1885 ثابت کرد. [11]
در سال 1900 دیوید هیلبرت مجموعه معروف خود را از مشکلات ارائه داد . هفتم از این ، و یکی از سخت ترین در برآورد هیلبرت، در مورد برتری از تعداد فرم خواسته ب که در آن و ب جبری هستند، است صفر یا یک، و ب غیر منطقی است. در سال های 1930، الکساندر گلفوند [12] و تئودور اسنایدر [13] ثابت کردند که همه چنین تعداد در واقع با استفاده از یک تابع کمکی غیر صریح که متعلق به لژیانه سیگل بود، به طور تعجب آور بود . این نتیجه،قضیه گلفوند-اشنایدر ، اثبات تعادل اعداد مانند e π و ثابت گلفوند-اشنایدر .
نتیجه بزرگ بعدی در این زمینه در دهه 1960 اتفاق افتاد، زمانی که آلن بیکر پیشرفتی را در مورد مشکل گلفوند در فرم های خطی در لگاریتم ها انجام داد . خود گلفوند توانست کمترین حد پایین را برای کمیت پیدا کند
جایی که همه چهار ناشناخته جبری هستند، αs که نه صفر و نه و βs غیر منطقی است. با این حال، پیدا کردن مرزهای مشابه مشابه برای مجموع سه یا چند لگاریتم، گلفوند را از بین برد. اثبات قضیه بیکر حاوی محدودیت هایی است که حل مسئله شماره کلاس گاوس برای کلاس اول در روند است. این کار برای استفاده از آن در حل معادلات دیوفاتن، مدال Baker فیلدرا به دست آورد . از یک دیدگاه نظری تعداد عاملی کاملا بنیادی، بیکر ثابت کرده است که اگر α 1 ، ...، α n اعداد جبری باشند، هیچ یک از آنها صفر یا یک و β 1 ، ...، β n اعداد جبری مانند 1، β 1 ، ...، βn براساساعداد منطقیبه صورت خطی مستقل است و سپس تعداد آن است
متعالی است [14]
تکنیک های دیگر: کانتور و زیلبر [ ویرایش ]
در دهه 1870، گرنت کانتور شروع به توسعه نظریه مجموعه کرد و در سال 1874 یک مقاله را به اثبات رساند که اعداد جبری را می توان به صورت یک به یک با مجموعه ای از اعداد طبیعی قرار داد و به این ترتیب مجموعه اعداد متعال باید شود غیر قابل شمارش . [15] بعدا، در سال 1891، کانتور از استدلال مرسوم آشنا بیشتر برای اثبات نتایج مشابه استفاده کرد. [16] در حالی که نتیجه کانتور اغلب به عنوان صرفا موجودی و به این ترتیب برای ساخت یک عدد متعالی، غیر قابل استفاده است، [17] [18]شواهد موجود در هر دو مقاله فوق به روش های ساخت اعداد متعالی می پردازند. [19]
در حالی که کانتور از نظریه مجموعه برای اثبات فراوانی اعداد متعالی استفاده کرده است، توسعه اخیر، استفاده از نظریه مدل در تلاش برای ثابت کردن یک مشکل حل نشده در نظریه اعداد متعال است.مشکل این است که تعیین درجه فرامنطقه میدان
برای اعداد پیچیده x 1 ، ...، x n که به صورت خطی مستقل از اعداد منطقی هستند. استفان اجانوئلحدس زده که جواب این است حداقل N ، اما هیچ مدرک شناخته شده است. در سال 2004،بوريس زيلبر مقاله اي را چاپ كرد كه از تكنيك هاي نظري مدل براي ساختن ساختار استفاده مي كرد كه بسيار شبيه به تعداد پيچيده اي است كه با عملكرد افزودن، ضرب كردن و انعكاس، عمل مي كند.علاوه بر این، در این ساختار انتزاعی فرضیهاجانوئل واقعا وجود دارد. [20] متاسفانه هنوز مشخص نشده است که این ساختار در حقیقت همان عدد پیچیده با عملیات ذکر شده است. ممکن است فرضیه اجانوئلl نامعلوم باشد و برخی از ساختار انتزاعی دیگری وجود دارد که رفتار بسیار مشابهی با اعداد پیچیده دارد، اما در مورد فرضیه اجانوئل. زیلبر معیارهای متعددی را ارائه داد که می توانست ثابت کند ساختار مورد نظر C بود ، اما نمی توانست به اصطلاح معیار انحصاری نمایشگر شدید اثبات کند. ساده ترین مورد از این اصل تا به امروز ثابت شده است، [21] اما اثبات آن است که آن را در عمق کامل مورد نیاز برای تکمیل اثبات حدس.
رویکردها [ ویرایش ]
یک مشکل معمول در این زمینه ریاضیات این است که آیا یک شماره داده شده متعالی باشد یا خیر. کانتور از یک استدلال قدرتمندی استفاده کرد تا نشان دهد که تنها شمارا شمارش جبری جسمی وجود دارد و از این رو تقریبا همه اعداد متعالی هستند. به این ترتیب، مقادیر متعارف، موارد معمول را نشان می دهند. حتی ممکن است اثبات کند که یک عدد معین متعالی است (یا حتی غیرعقلایی)، بسیار دشوار است.
به همین علت نظریه متعالیه اغلب به رویکرد کمی بیشتر عمل می کند. بنابراین با توجه به تعداد پیچیده ای α می توان از چگونگی نزدیک بودن α به یک عدد جبری استفاده کرد. به عنوان مثال، اگر فرض شود که عدد α جبری است، می تواند نشان دهد که باید درجه بسیار بالایی داشته باشد یا حداقل چندجمله ای با ضرایب بسیار بزرگ؟ در نهایت اگر ممکن است نشان دهیم که هیچ درجه محدود یا اندازه ضریب کافی نیست، این عدد باید فراتر از حد باشد. از آنجایی که عدد α فوق العاده است اگر و فقط اگر P (α) ≠ 0 برای هر چندجملهای غیر صفر P با ضرایب عدد صحیح، این مشکل را می توان با تلاش برای پیدا کردن معیارهای پایین تر از فرم
که در آن به سمت راست برخی از عملکرد مثبت بسته به برخی از اندازه گیری است از اندازه از ضرایب از P ، و آن درجه د ، و به طوری که این کران پایین به همه اعمال P ≠ 0. چنین محدود است که به نام اندازه گیری تعالی .
در مورد d = 1، تقریب "کلاسیک" دیوفانتین با درخواست مرزهای پایین برای

روش های تئوری تعالی و تقریب دیوفانتین بسیار مشترک هستند: آنها هر دو از مفهوم تابع کمکی استفاده می کنند .
نتایج عمده [ ویرایش ]
قضیه گلفوند-اشنایدر پیشرفت عمده ای در نظریه تعالی در دوره 1900-1950 بود. در 1960s روش آلن بیکر در اشکال خطی در لگاریتم از اعداد جبری بازگشت از دنیای مردگان نظریه تعالی، با برنامه های کاربردی به مشکلات کلاسیک متعدد و معادلات سیاله .
مشکلات باز [ ویرایش ]
در حالی که قضیه گلفوند-اشنایدرثابت کرد که یک کلاس بزرگ از اعداد فوق العاده بود، این کلاس هنوز قابل شمارش بود. بسیاری از ثابت های ریاضی به خوبی شناخته شده هنوز شناخته شده نیستند و در برخی موارد حتی شناخته نمی شوند که آیا آنها منطقی یا غیر منطقی هستند. لیست جزئی در اینجا می توانید پیدا کنید .
یک مشکل عمده در نظریه متعال، نشان دادن آن است که یک مجموعه خاص از اعداد به طور جبری مستقل است، نه فقط نشان دادن اینکه عناصر فردی متعالی هستند. بنابراین، در حالیکه می دانیم که eو π متعلق به فراموشی هستند که به این معنی نیست که e π فراتر از عبارات و ترکیبات دیگر این دو است (به غیر از e π ، ثابت گلفوند که شناخته شده به فراموشی است). یکی دیگر از مشکلات عمده این است که با اعداد مربوط به عملکرد نمایشی برخورد می شود. نتایج اصلی در نظریه متعال، تمایل به چرخش در اطراف e دارند و تابع لگاریتم است که به این معنی است که روشهای کاملا جدیدی برای مقابله با اعداد است که نمیتوان از طریق این دو عنصر به صورت ابتدایی بیان کرد.
فرضیه اجانوئل اولین مسئله ی این مشکلات را تا حدی حل می کند که به استقلال جبری مربوط می شود و حقیقتا تایید می کند که e π متعالی است. با این حال، هنوز هم در اطراف تابع نمایشی حرکت می کند و بنابراین لزوما با تعداد هایی مانند ثابت آپیر یا ثابت یولر- ماسکرانی ارتباط ندارد . یکی دیگر از مشکل بسیار حل نشده مشکل به اصطلاح ثابت یا هویت است . [22]
ثابت گلفوند-اشنایدر یا هیلبرت تعداد [1] است دو به قدرت از ریشه دوم دو :
2 √ 2 =2.665 144 142 690 225 188 650 297 249 8731 ...
که به یک ثابت شد عدد متعالی توسط رودیون کوزمین در سال 1930. [2] در سال 1934، الکساندر گلفوند و تئودور اشنایدر به طور مستقل اثبات کلی تر قضیه گلفوند-اشنایدر ، [3] که بخشی از حل مسئله هفتم هیلبرت زیر توضیح داده شده.
فهرست
خواص [ ویرایش ]
جذر ثابت گلفوند-اشنایدر تعداد متعالی است

این همان ثابت می تواند مورد استفاده قرار گیرد تا ثابت کند که "یک افزایش نامعقول به یک قدرت غیر منطقی ممکن است منطقی باشد"، حتی بدون اینکه اولین اثباتش برتری آن باشد. اثبات به شرح زیر است: یا √ 2 √ 2 منطقی است، که ثابت می کند قضیه، یا غیر منطقی است (همانطور که معلوم می شود)، و سپس
یک غیر منطقی است به قدرت غیر منطقی که منطقی است، که قضیه را اثبات می کند. [4] [5] اثبات سازنده نیست ، زیرا آن را نمی گوید که کدام دو مورد درست است، اما بسیار ساده تر از اثباتکوزمین است .
مسئله هفتم هیلبرت [ ویرایش ]
مقاله اصلی: مسئله هفتم هیلبرت
بخشی از هفتم و بیست و سه مسائل هیلبرت مطرح در سال 1900 به اثبات برساند، و یا پیدا کردن یک مثال نقض به، این ادعا که بود ب همیشه استعلایی برای جبری ≠ 0، 1 و غیر منطقی جبری ب .در این آدرس به دو مثال صریح اشاره کرد، یکی از آنها ثابت بودن ثابت گلفوند-اشنایدر2 √ 2 است .
در سال 1919، او سخنرانی در نظریه اعداد و سخنرانی از سه فرضیه: فرضیه ریمان ، آخرین قضیه فارما و ترانسدانس 2 √ 2 . او به مخاطبان اشاره کرد که هیچ کس در سالن انتظار ندارد تا به اندازه کافی بلند شود تا اثبات این نتیجه نهایی را ببیند. [6] اما اثبات برتری این عدد توسط کوزمیندر سال 1930 [2] به خوبی در طول عمر خود هیلبرت منتشر شد. بطور مثال، کوزمین اثبات کرد که در آن exponent b یک معادل غیر منطقی است که بعدها به یک غیر منطقی دلخواه b توسطگلفوند و توسط -اشنایدر.
ثابت گلفوند
از ویکیپدیا، دانشنامه آزاد
نه با گلفوند-اشنایدر ثابت شود .
در ریاضیات ، ثابت گلفوند ، نام بعد از الکساندر گلفوند ، e π است، یعنی به قدرت π افزایش یافته است . مانند e و π ، این ثابت یک عدد متعالی است . این اولین بار توسط گلفوند ساخته شد و در حال حاضر می تواند به عنوان کاربردی از قضیه گلفوند-اشنایدر تلقی شود ،
که در آن من است واحد موهومی . از آنجا که - من جبری است، اما منطقی نیست، E π متعالی است. ثابت در هفتمین مسئله هیلبرت ذکر شده است . [1] یک ثابت مرتبط است
فهرست
ارزش عددی [ ویرایش ]
گسترش اعشاری ثابت گلفوند شروع می شود
ساخت و ساز [ ویرایش ]
اگر یکی تعریف کند 
برای 
به سرعت همگرا می شود
ادامه گسترش کسری [ ویرایش ]
این بر اساس رقم ها برای تقسیم ساده ادامه می یابد :
همانطور که توسط دنباله A058287 عدد صحیح داده شده است .
اموال هندسی [ ویرایش ]
حجم N توپ بعدی (یا N -Ball )، توسط داده
جایی که 

و، جمع کردن تمام توپ واحد ( R = 1) حجم ابعاد حتی می دهد [4]
ثابت یا مشابه آن [ ویرایش ]
ثابت رامانوجان [ ویرایش ]
این به عنوان ثابت رامانوجان معروف است. این یک کاربرد از اعداد هگنر است ، که در آن 163 شماره هجنر است.
شبیه به 

همانطور که رامانوجان ریاضیدان هندی بود که اولین بار این عدد تقریبا عدد صحیح را پیش بینی کرد، بعد از او نامگذاری شد، هر چند که این شماره اولین بار توسط ریاضیدان فرانسوی چالزهرمیت در سال 1859 کشف شد.
نزدیک شدن تصادفی، در حدود 0.000 000 000 000 75 عدد 
و،
جایی که 
که توضیح می دهد که چرا 

(برای جزئیات بیشتر در این اثبات، با مقاله در مورد شماره هایگنر مشورت کنید .)
شماره 
گسترش اعشاری از 
علیرغم این که تقریبا عدد صحیح 20 است، هیچ توضیحی برای این واقعیت داده نشده است و بر این باور است که یک تصادف ریاضی است.
شماره 
همانطور که با 

گسترش اعشاری برای 
شماره 
گسترش اعشاری از 
معلوم نیست این عدد متعالی است یا نه. توجه داشته باشید که، طبق قضیه گلفوند-اشنایدر ، ما می توانیم به طور قطعی آن را بیابیم




در شرایطی که 







شماره 
گسترش اعشاری توسط A049006 داده می شود :
به دلیل همبستگی، می توان از قضیهگلفوند-اشنایدر استفاده کرد تا ثابت کند که ریشه مربع متقاطع ثابت گلفوند نیز متعال است:



همچنین نگاه کنید به [ ویرایش ]
تئوری تعداد ترانسدادن ، مطالعه سوالات مربوط به اعداد متعالی است
شنامه آزاد
این نام از گمرک نامگذاری شرقی Slavic استفاده می کند ؛ خانوادگی گریگوریویچ است و نام خانوادگی Chebotaryov است.
نیکولای چبوتارف | |
|---|---|
 نیکلای چبوترایف (به سمت چپ) با دانشجویان | |
| بدنیا آمدن | 15 ژوئن 1894 Kamianets-Podilskyi ، امپراتوری روسیه(امروزه اوکراین ) |
| فوت کرد | 2 ژوئیه 1947 (53 ساله) |
| ملیت | اتحاد جماهیر شوروی |
| آلما مادر | دانشگاه دولتی کیف |
| شناخته شده برای | تئوری تراکم چبوتارف |
| حرفه علمی | |
| زمینه های | ریاضیات |
| موسسات | دانشگاه ایالتی کازان |
| مشاور دکترا | دمیتری گریو |
| دانشجویان دکتری | علامت گذاری به عنوان کریین Naum Meiman |
نیکولای گرگوریویچ چبوتاروف (اغلب به نام Chebotarov یا Chebotarev ، روسی : Николай Григорьевич Чеботарёв ، اوکراین : Микола Григорович Чоботарьов ) (15 ژوئن [ OS 3 ژوئن 1894 - 2 ژوئیه 1947] یکریاضیدان روسی و شوروی بود . [1] او بهتر است برای قضیه چگالی چبوتاروف شناخته شده است . [2]
او دانشجوی دمیتری گریو ، یک ریاضیدان روسی بود . [3] چبوتاروف بر روی جبر چندجملهای کار کرد، به ویژه بررسی توزیع صفرها.او همچنین نظریه گالوئیس را مطالعه کرد و کتاب درسی را با عنوان The Basic Gaois Theory نوشت . ایده های او توسط امیل آرتین برای اثبات قانون متقابل Artin استفاده شد . [4] او با دانش آموز آناتولی Dorodnov نوشتن در تعاریف چهارگوشه لونه ، [5] کارکرد و ثابت کرد که این حدس به عنوان قضیه Chebotaryov در ریشه های وحدت شناخته شده است .
زندگی زودهنگام [ ویرایش ]
نیکولای چبوتارف در 15 ژوئن 1894 در Kamianets-Podilskyi ، امپراتوری روسیه (امروزه اوکراین ) متولد شد . او در سال 1912 در دانشگاه کیف در رشته ی فیزیک و ریاضیات وارد شد. در سال 1928 پروفسور دانشگاه کازان شد و بقیه عمر خود را باقی گذاشت. او در 2 ژوئیه 1947 درگذشت. او بیخدای بود. [6] در 14 مه 2010، یک پلاک یادبود برای نیکلای چبوتاریف در ساختمان اداری اصلی دانشگاه ملی اودسا II Mechnikov منتشر شد . [7]
در ریاضیات ، به ویژه در نظریه هموتوپی در توپولوژی جبری ، به هموتوپیتوسیع دادن (همچنین به عنوان یک نمونه از شناخته شده توسیع و یا اصل پوشش هموتوپی) شرایط فنی در است تابع پیوسته از یک فضای توپولوژیک الکترونیکی به یک دیگر، B . این طرح برای حمایت از تصویر E "بالای" B با اجازه دادن به همگانی در B اتفاق می افتد تا "طبقه بالا" به E منتقل شود .
به عنوان مثال، یک نقشه پوشش دارای ویژگی منحصر به فرد محلی توسیع مسیر به یک ورق داده شده است؛ منحصر به فرد بودن این است که الیاف یک نقشه پوشش، فضاهای مجزا هستند . اموال بلند پروازی هماتوپوپی در بسیاری از موارد، مانند طرح بندی در یک بسته نرم افزاری ، بسته نرم افزاری فیبر یا فیبریس ، نگهداری می شود، جایی که نیازی به هیچ راهی برای بلند کردن نیست.
فهرست
تعریف رسمی [ ویرایش ]
فرض کنید از هم اکنون تمام نقشه ها توابع مداوم از یک فضای توپولوژی به دیگری هستند. با یک نقشه




برای هر
، و
برای هر نقشه
توسیع
(به عنوان مثال، به طوری که
)،
یک هموتوپی وجود دارد ![{\ tilde {f}} \ colon X \ times [0،1] \ to E](https://wikimedia.org/api/rest_v1/media/math/render/svg/266c2d08e6a76d353c000758d59992ec47c8ff27)



نمودار زیر این وضعیت را نشان می دهد.
مربع بیرونی (بدون فلش نقطه ی نقطه ای) اگر و فقط اگر فرضیه ها از ویژگی های بلند بلند درست است، حرکت می کند. توسیع
اگر نقشه


توجه داشته باشید که این تعریف فیبریسیون به معنای Hurewicz است ، که محدودتر از فیبریسیون به معنای Serre است ، برای آن که تنها برای
تعاریف: توسیع هموتوپی [ ویرایش ]
تعاریف مشترک توسیع هماتوپوپی و گسترش هموتوپی وجود دارد . با توجه به یک جفت فضا
![T \ colon = (X \ times \ {0 \}) \ cup (Y \ times [0،1]) \\ subseteq \ X \ times [0،1]](https://wikimedia.org/api/rest_v1/media/math/render/svg/168b6da9c1ac353f57460f766fa84ab0c89702b1)


برای هر
، و
برای هر بلند شدن
از
،
یک هماتومی وجود دارد ![{\ tilde {f}} \ colon X \ times [0،1] \ to E](https://wikimedia.org/api/rest_v1/media/math/render/svg/266c2d08e6a76d353c000758d59992ec47c8ff27)




مالکیت بلند پروازی هموتوپی 



خواص توسیع هموتوپی از 



همچنین نگاه کنید به [ ویرایش ]
در ریاضیات ، گروه های هموتوپی در توپولوژی جبری برای طبقه بندی فضاهای توپولوژیکی استفاده می شود . اولین و ساده ترین گروه هماتوپوپی، گروه اساسی است که اطلاعات مربوط بهحلقه ها را در یک فضای ثبت می کند . به طور مستقیم، گروه های همگانی می توانند اطلاعات مربوط به شکل پایه یا سوراخ یک فضای توپولوژیک را ثبت کنند.
برای تعریف گروه n -th گروه های هموتوپی، نقشه های حفظ پایه نقطه از یک کره n -بعدی (با نقطه پایه ) به یک فضای داده شده (با نقطه پایه) به کلاس های همسان سازی ، به نام کلاس های هموتوپی جمع می شوند . دو تطبیق هموتوپیک هستند اگر بتوان آن را به طور مداوم به شکل دیگر تغییر داد. این کلاسهای همگانی ، گروهی را تشکیل می دهند که به نام گروه های هموتوپی n است .
مفهوم هماتوپی مسیرها توسط کامیل اردن معرفی شد . [1]
فهرست
- 1مقدمه
- 2تعریف
- 3دنباله دقیق بلند یک فیبریس
- 4روش محاسبه
- 5فهرستی از روشهای محاسبه گروههای هماتوپوپی
- 6گروه هماتوپوپی نسبی
- 7مفاهیم مرتبط
- 8همچنین ببینید
- 9یادداشت
- 10منابع
مقدمه [ ویرایش ]
در ریاضیات مدرن آن است که مشترک به مطالعه دسته های مرتبط به هر شی از این دسته یک شی ساده که هنوز اطلاعات کافی در مورد موضوع مورد علاقه را حفظ است. گروه های هموتوپی به گونه ای هستند که گروه ها را به فضاهای توپولوژیکی مرتبط می کنند.
ترور
یک کره
این پیوند بین توپولوژی و گروه ها به ریاضیدانان امکان می دهد بینش های نظریه گروهی را بهتوپولوژی اعمال کند . به عنوان مثال، اگر دو اشیاء توپولوژیک دارای گروه های مختلف هماتوپوپی باشند، آنها نمی توانند یک ساختار توپولوژیکی مشابه داشته باشند؛ این واقعیت است که ممکن است اثبات شود که تنها با استفاده از معانی توپولوژیکی اثبات شود. به عنوان مثال، توور از قلمرومتفاوت است : توور دارای یک سوراخ است؛ حوزه نمی دهد با این حال، از آنجا که تداوم (مفهوم پایه توپولوژی) تنها با ساختار محلی در ارتباط است، می تواند به طور رسمی تعریف تفاوت جهانی را دشوار کند. با این وجود، گروههای همگانی هم اطلاعاتی درباره ساختار جهانی دارند.
به عنوان مثال: اول گروه هموتوپی از تورها یT است
زیرا پوشش جهانی تورهای اقلیدسی است


چرا که هر حلقه را می توان به یک نقشه ثابت متصل کرد (گروه های هموتوپی از حوزه ها را برای این و نمونه های پیچیده تر از گروه های همگانی تطبیق می دهیم).
از این رو توورها به حوزه نزدیك نیستند .
تعریف [ ویرایش ]
در 

که نقطه پایه a را به نقطه پایه ب ببندید . به طور خاص، کلاس های هم ارز توسط هموتوپی ها داده می شوند که در نقطه پایه کره ثابت هستند. به طور معادل، ما می توانیم π n ( X ) را به عنوان گروهی از کلاس های هموتوپی نقشه ها تعریف کنیم![{\ displaystyle g \ colon [0،1] ^ {n} \ to X}](https://wikimedia.org/api/rest_v1/media/math/render/svg/2958cf35a64fa9443f9d3630131ec10e0fc0a4e8)
ترکیب در گروه اساسی
برای

![{\ displaystyle f، g: [0،1] \ to X}](https://wikimedia.org/api/rest_v1/media/math/render/svg/a920e0286bc83e6886f12d67baa3c379609686c1)
ایده ترکیب در گروه اساسی این است که سفر نخستین مسیر و دوم به ترتیب، و یا به طور برابر، تنظیم دو حوزه خود را با هم. مفهوم ترکیب که ما برای گروه هومیوپاتی n می خواهیم یکسان است، با این حال اکنون دامنه هایی که ما با هم می چیند، مکعب هستند، و ما باید آنها را در کنار چهره چسب کنیم. بنابراین ما مجموع نقشه ها را تعریف می کنیم![{\ displaystyle f، g: [0،1] ^ {n} \ to X}](https://wikimedia.org/api/rest_v1/media/math/render/svg/42a801f149dc7c105ade1c13fd90ed52aeb1faf9)
برای تعریف مربوطه از لحاظ حوزه ها، مجموع را تعریف می کنیم 




اگر 


وسوسه آمیز است سعی کنید تعریف گروه های همگانی را ساده تر با نادیده گرفتن امتیازات پایه، اما معمولا برای فضایی که به سادگی متصل نیست ، حتی برای فضاهای مرتبط با مسیر کار نمی کند.مجموعه ای از کلاس های هماتوپوپی از نقشه ها از یک کره به یک فضای مرتبط با مسیر، گروه هومیوپاتی نیست بلکه اساسا مجموعه ای از مدارهای اساسی گروه گروه همولوگ است و به طور کلی هیچ ساختار گروهی طبیعی ندارد.
یک راه حل برای این مشکلات با تعریف گروههای هومیوپاتی بیشتر از فضاهای فیلتر شده و n- cubes فضاها مشخص شده است. این ها به ترتیب بهگروه های هموتوپی نسبی و گروه های هموتوپی n- adic وابسته هستند. هموتوپی بالاتر ون Kampen قضیه پس از آن یکی را قادر می سازد به استخراج برخی از اطلاعات جدید درگروه های هموتوپیو حتی در انواع هموتوپی. برای زمینه و مراجع بیشتر، نگاه کنید به "نظریه گروهی بالاتر و مراجع زیر.
دنباله دقیق دقیق یک فیبریس [ ویرایش ]
بگذارید p : E → B یک فیبری Serre با فیبر F با حفظ نقطه پایه باشد ، یعنی یک نقشه دارای خصوصیات Lifting هموتوپی با توجه به مجموعه های CW . فرض کنید که B ارتباط مسیر است. سپس یک توالی دقیق از گروه های هموتوپی وجود دارد
در اینجا نقشه هایی که شامل π 0 هستند، homomorphisms گروهی نیستند، به این دلیل که π 0 گروه نیستند، اما دقیقا به این معنی است که تصویر برابر با هسته است.
مثال: فیبری Hopf . اجازه دهید B برابر S 2 و E برابر S 3 باشد. اجازه دهید ص شود هاف fibration ، که دارای فیبر S 1 . از ترتیب دقیق دقیق
و این واقعیت که π n ( S 1 ) = 0 برای n ≥ 2، پیدا می کنیم که (π n ( S 3 ) = π n ( S 2 برای n ≥ 3. به طور خاص،
در مورد یک فضای پوشش، زمانی که فیبر گسسته است، ما این را داریم که ((π n ( E ) برای n > 1 π n ( B ) است ، که π n ( E ) به صورت تزریقی به π n ( B ) برای همه ی مثبت n و زیر گروه π 1 ( B ) که مربوط به تعبیر π 1 ( E ) است در اقلیت با عناصری از فیبر دارا است.
هنگامی که فیبرینگ فیبر نقشه برداری است ، یا دوگانه، همرفت شدن مخروط نقشه برداری است ، سپس دنباله دقیق (یا دوگانه) و هماهنگ با توالی Puppe داده می شود .
روش های محاسبه [ ویرایش ]
محاسبه گروه های همگانی تقریبا بسیار دشوارتر از برخی دیگر از توابع هماتوپوپی است که در توپولوژی جبری آموخته شده اند. بر خلاف قضیه سیفرت-ون Kampen اساسی برای گروه و قضیه برداشتن برای همسانی مفرد و های cohomology ، هیچ راه ساده شناخته شده برای محاسبه گروه های هموتوپیاز یک فضا با شکستن آن را به فضاهای کوچکتر وجود دارد. با این حال، روش های توسعه یافته در دهه 1980 شامل قضیه نوع ون کپن برای گروه های هومیوپاتی بالاتر اجازه داده است محاسبات جدید بر روی انواع هموتوپیو به همین ترتیب گروه های هموتوپی. برای نتیجه ی نمونه ای از مقاله ی الیس و میهیلوف که در سال 2008 ذکر شده است را ببینید.
برای بعضی از فضاها، مانند توری ، همه گروه های هماتوپوفی بالاتر (یعنی گروه های هماتوپوپی دوم و بالاتر) بی اهمیت اند. این فضاهای به اصطلاح فضایی است . با این وجود، علیرغم تحقیقات شدید در محاسبه گروه های هماتوپوپی از حوزه ها، حتی در دو بعد، لیست کامل شناخته شده نیست. برای محاسبه حتی گروه چهارم هموتوپی S 2 نیاز به تکنیک های پیشرفته ای بسیار بیشتر از تعاریف ممکن است. به طور خاص دنباله طیف Serre برای این منظور ساخته شده است.
گروه های خاص هموتوپیاز فضاهای N مرتبط را می توان با مقایسه با گروه های همولوگ از طریق قضیه Hurewicz محاسبه می شود .
فهرستی از روشهای محاسبه گروههای هموپتوپی [ ویرایش ]
- دنباله دقت طولانی از گروه های هموتوپیاز یک فیبراسیون.
- قضیه Hurewicz ، که دارای چندین نسخه است.
- قضیه Blakers-Massey ، همچنین به عنوان اصلاح برای گروه هموتوپیشناخته شده است.
- Theorem تعلیق Freudenthal ، یک نتیجه از برداشت برای گروه های هموتوپی.
گروه های هماتوپاتی نسبی [ ویرایش ]
همچنین یک تعمیم مفیدی از گروههای همگانی وجود دارد 


ساخت و ساز مبتنی بر مشاهده است که برای گنجاندن






عناصر چنین گروهی، کلاسهای هماتوپاتی نقشه های مبتنی است 


این گروه ها abelian برای n ≥ 3 هستند، اما برای n = 2، گروه بالا از ماژول متقاطع با گروه پایین π 1 ( A ) تشکیل می شود.
همچنین یک توالی دقیق از گروه های هموتوپینسبی وجود دارد که می تواند از طریق توالی Puppe حاصل شود :
مفاهیم مرتبط [ ویرایش ]
گروه های گرایی برای تئوری همگانی تطبیق دارند ، که به نوبه خود باعث توسعه مدل های مدل شده است . ممکن است گروههای همولوگ اپتیکال برای مجموعه های ساده را تعریف کنیم .
همچنین نگاه کنید به [ ویرایش ]
لئونید Ivanovich Plyushch ( اوکراینی : Леонід Іванович Плющ ، IPA: plʲuʃtʃ ؛ روسی : Леонид Иванович Плющ ، 26 آوریل 1938، نرین ، کیرشیز SSR - 4 ژوئن 2015، Bessèges ، فرانسه ) یک ریاضیدان اوکراین و مخالف شوروی بود .
زندگی اولیه و حرفه ای [ ویرایش ]
لئونید پیلچ در سال 1938 در نیویورک ، کوریزیا ، به یک خانواده طبقه کارگر اوکراین متولد شد . پدرش به عنوان سرپرست راه آهن مشغول به کار شد و در سال 1941 در جلوی درگذشت . دوران کودکی لئونید با سل خارج شده از استخوان، که او در سن 8 سالگی قرارداد بست. [2] [3]
Plyushch از دانشگاه کیف در سال 1962 با مدرک ریاضی فارغ التحصیل شد. در آخرین سال تحصیل او علاقه مند به مدل سازی ریاضی سیستم های بیولوژیکی، به ویژه بیماری روحی بود که او با کمک یک کامپیوتر مدل سازی کرد. این کار یک مشکل را ثابت کرد، اما Plyushch مقاله هایی در مورد مدل سازی و تنظیم سیستم های بیولوژیک ساده مانند سطح قند خون منتشر کرد. او در نهایت توسط موسسه Cybernetics از آکادمی علوم اتحاد جماهیر شوروی استخدام شد ، که اغلب به حل مسائل مختلف برای برنامه فضایی شوروی مشغول بود . [4] [5]
فعالیت های غیر رسمی [ ویرایش ]
Plyushch با مخالفت با موضع عمومی در مورد موضوع داغ سیاسی از زمان. در سال 1968، با ارسال یک نامه به Komsomolskaya Pravda ، که منتشر نشد، علیه سوء رفتار پروندهGalanskov-Ginzburg اعتراض کرد . هنگامی که نیروهای شوروی در سال 1968 به چکسلواکی حمله کردند ، پلوشچ با 16 مخالف دیگر شوروی، اعلامیه همبستگی با جنبش دموکراتیک در چکسلواکی را امضا کرد. در همین سال او به گروه ابتکار دفاع از حقوق بشر در اتحاد جماهیر شوروی پیوست و در نامه ای به کمیسیون حقوق بشر سازمان مللاز او می خواهد تا نقض های اتحاد جماهیر شوروی را درباره حق داشتن اعتقادات مستقل و تبلیغ آنها به وسیله ی قانونی تحقیق کند. پلوشچ یکی از پانزده تن از اعضای کمیته حقوق بشر سازمان ملل بود. [6] با توجه به مقاومت از مواضع سیاسی خود، او را از موسسه سایبرنتیک در سال 1968 برکنار شد، و کا گ ب مصادره تعدادی از نسخه های خطی و او را مورد بازجویی چندین بار. [7] [8]
محاکمه و زندان [ ویرایش ]
او در ژانویه 1972 به اتهام فعالیت ضد شوروی دستگیر شد و یک سال قبل از محاکمه او زندانی شد. در جریان دادگاه، دادگاه نشسته در دوربین و در شرایطی که متهم کرد. اگرچه هیچ شاهد متخصصی از هر نوع نامگذاری نداشته است، Plyushch اعلام کرد دیوانه و دستور داده شد که "برای درمان در نوع خاصی از بیمارستان فرستاده شود". او در یک بند به شدت قفل شده بود روانیبیماران در دنیپروپتروفسک بیمارستان ویژه روانپزشکی که در آن دوز بالایی از هالوپریدول ، انسولین و داروهای دیگر تجویز شد که به طور موقت او را از خواندن و نوشتن ناتوان. [9] [10]سه کمیته که پس از یک سال بازداشت او را مورد بررسی قرار دادند، یکی از آنها تحت عنوان آندره اسنژنوفسکی سرپرستی کرد ، او را از «تصورات اصلاح طلب» با «عناصر مسیح» و « اسکیزوفرنی مبهم» رنج می برد . [11] در 28 نوامبر سال 1976، پلوشچ گفت، مسکو از پیمان امنیتی هلسینکی برای بهبود وضعیت اقتصادی خود استفاده می کند و در عین حال افزایش سرکوب مخالفان سیاسی را نیز افزایش داده است. [12]
در حالی که او در زندان بود، با تاتیانا کندورویچ ارتباط برقرار کرد. [13] نامه های پلوشچ به او بعدا مبنای کتاب «مورد لئونید پیلشچ » را که در سال 1974 توسط ناشر آمستردام به زبان روسی منتشر شد، تشکیل داد و دو سال بعد به انگلیسی ترجمه شد و در مجلات علمی اخلاق پزشکی مورد توجه قرار گرفت. [9] [14] زندان او باعث اعتراضات بین المللی شد، از جمله نامه ای توسط 650 ریاضیدان آمریکایی به سفارت شوروی. [10] هنری کارتان ، این رویداد را به شرکت کنندگان در کنگره بین المللی ریاضیدانان 1974 ، که در ونکوور برگزار شد، آورده است. [15] : 788 سازمان عفو بین الملل روز جهانی برای Plyushch به در آوریل 1975 تحت حمایت، [13] و آندره ساخاروف نیز از طرف او التماس کرد. [16]
آزادی و زندگی بعد [ ویرایش ]
او در نهایت مجاز به ترک اتحاد جماهیر شوروی با خانواده اش در سال 1976 شد. [13] ورود او به غرب باعث افزایش اصطکاک بین روانپزشکان غربی و شوروی شد و منجر به محکومیت اعمال شوروی توسط انجمن جهانی روانپزشکی در کنگره جهانی ششم شد. روانپزشکی [17] [18] در یک کنفرانس مطبوعاتی در پاریس، Plyushch به یاد خاطره ای از اثرات بازداشت و داروهای او اشاره کرد: [19]
من با ترس از پیشرفت روزانه تخریب من متوجه شدم. من علاقه مند به سیاست، و سپس در مشکلات علمی، در نهایت همسر و فرزندانم را از دست دادم. سخنرانی من تار شد؛ حافظه من بدتر شد. در آغاز، به شدت به رنج های دیگر بیماران واکنش نشان دادم. در نهایت من بی تفاوت شدم تنها افکار من از توالت، تنباکو و رشوه برای پرستاران مرد بود که اجازه دادم یک بار دیگر به توالت بروم. سپس من شروع کردم به یک فکر جدید: "من باید به یاد داشته باشید همه چیز را در اینجا، من خودم گفتم، به طوری که من بعد از آن می توانید بگویید."
Plyushch در سال 1977 عضو گروه اوکراین هلسینکی شد و حقوق بشر را در بومی خود در اوکراین ارتقا داد. [20]
در 23 جولای 1978، پلوشچ از اوکراین در استرالیا بازدید کرد و به پارلمان استرالیا گفت . [21]
در سال 1979، با کمک همسرش، Plyushch کتاب خود را « کارناوال تاریخی» منتشر کرد : بیوگرافی دائمی، که در آن او توضیح داد چگونه او و دیگر مخالفان به بیمارستان های روانپزشکی متعهد بودند. [22] در همان سال، این کتاب به زبان انگلیسی ترجمه شد. [23] در سال 1980، آندری Snezhnevsky ، که عضو همکار کالج سلطنتی روانپزشکی بود، توسط همکاران بریتانیایی اش دعوت به پاسخ انتقاد مربوط به Plyushch و سایر مخالفان. او این کار را نکرد و به جای آن استعفا داد. [24]
بعدا در زندگی، اگر چه او اعتقادات کمونیستی را حفظ کرد، [13] پلوشچ از انتشارات ضدتعالی در سایر کشورهای کمونیست، از جمله ویتنام حمایت کرد . [25]
Plyushch در تاریخ 4 ژوئن 2015 در Bessèges ، [1] فرانسه . [26] [27] مرگ او توسط یکی از دوستان و دیگر مخالف سابق شوروی، آریا Ginzburg گزارش شد. [28]
هنری کارتان
از ویکیپدیا، دانشنامه آزاد
هنری کارتان | |
|---|---|
 هنری کارتان در سال 1968 | |
| بدنیا آمدن | هنری پل کارتان 8 ژوئیه 1904 نانسی ، فرانسه |
| فوت کرد | 13 اوت 2008 (104 ساله) پاریس ، فرانسه |
| ملیت | فرانسوی |
| آلما مادر | École Normale Supérieure |
| شناخته شده برای | قضیه Cartan A و B |
| جوایز | جایزه گرگ (1980) |
| حرفه علمی | |
| زمینه های | ریاضیات |
| موسسات | دانشگاه پاریس |
| مشاور دکترا | پل مونتل |
| دانشجویان دکتری | جین پال بنز کری پری کارتیه جین سرف ژاک دنی آدرین دوودی پیر دولتو روجر گودمن مکس کروبی ژان لوئیس کوزول ژان پیر سر رنه توم |
هنری پل کارتان ( فرانسوی: kaʁtɑ ؛ 8 جولای 1904 - 13 آگوست 2008) [1] یک ریاضیدان فرانسوی بود که کمک زیادی بهتوپولوژی جبری کرد . او پسر ریاضیدان فرانسوی الی کارتان [2] و برادر آهنگساز جین کارتن بود.
فهرست
زندگی [ ویرایش ]
کارتن در Lycée Hoche در ورسای ، و سپس در École Normale Supérieure در پاریس، دریافت دکترای خود را در ریاضیات. او در دانشگاه استراسبورگ از نوامبر 1931 تا زمان شروع جنگ جهانی دوم تدریس کرد ، و پس از آن او در دانشگاه های فرانسوی دیگر تحصیلات علمی خود را صرف کرد، بخش عمده ای از زندگی کاری او در پاریس را صرف کرد .
کارتل برای کار در توپولوژی جبری ، به ویژه در عملیات هماهنگی ، روش «کشتن گروه هماتوپوپی » و هماهنگی گروه شناخته شده است. سمینار وی در پاریس در سالهای پس از سال 1945 تحت تاثیر چندین متغیر پیچیده ، نظریه مخروطی ، توالی طیفی و جبر هموسیلی قرار گرفت ، به طوری که عمیقا تحت تاثیر ژان پیر سار ، آرماند بورل ، الکساندر گروتینیک و فرانک آدامز ، در میان دیگر رهبران چراغ نسل جوان. تعداد دانشجویان رسمی او کوچک بود، اما شاملآدریان دوودی ، راجر گودمن ، مکس کروبی ، ژان لوئیس کوزول ، ژان پیر سر و رنه توم . [3]
کارتان همچنین یکی از بنیانگذاران گروه بوربکی و یکی از فعال ترین شرکت کنندگان او بود. کتاب او با الگوریتم همگام ساموئل آیلنبرگ [4] یک متن مهم بود و موضوع را با استفاده از تئوری دسته بندی با سطح متوسطی از انتزاع در نظر گرفت .
کارتل از نفوذ او برای کمک به به دست آوردن آزادی برخی از ریاضیدانان ناراضی ، از جمله لئونید Plyushch و خوزه لوئیس Massera استفاده از . او برای اهداف انسانی خود، جایزه Pagels از آکادمی علوم نیویورک را دریافت کرد . [5]
مدل کارتان در جبر پس از کارتان به نام.
کارتن در سن 13 سالگی درگذشت 13 اوت 2008 بود. مراسم تشییع جنازه او در روز چهارشنبه در تاریخ 20 آگوست در شهر Die، Drome برگزار شد . [2]
افتخارات و جوایز [ ویرایش ]
Cartan افتخارات و جوایز متعددی از جمله جایزه گرگ را در سال 1980 دریافت کرد. او سخنگوی ICM در سال 1932 در زوریخ و یک سخنگوی کمیته ICM در سال 1950 در کمبریج، ماساچوست [6] و در سال 1958 در ادینبورگ بود. [7] از سال 1974 تا زمان مرگ وی عضو آکادمی علوم فرانسه بود . او یک عضو خارجی بود آکادمی فنلاندی علم و نامه ، سلطنتی دانمارک آکادمی علوم و نامه ها، انجمن سلطنتی لندن ، آکادمی علوم روسیه ، سلطنتی سوئد آکادمی علوم ، ایالات متحده آکادمی ملی علوم، آکادمی علوم لهستان و سایر آکادمی ها و جوامع.
نشریات منتخب [ ویرایش ]
- در سالهای 1928 و 1928، برنامه های کاربردی و برنامه های کاربردی ،
- گروه های تحرکی تحولات ، 1935.
- در سال 1940، کلاس های آموزشی و تربیت بدنی در سال 1940 برگزار می شود.
- اسپرز فیبرس و هماتوپی ، 1949-1950.
- Cohomologie des groupes، مجموعه طیفی، faisceaux ، 1950-1951.
- Algèbres d'Eilenberg - Mac Lane et Homotopie ، 1954-1955.
- خودروسازان Fonctions ، 1958-1958.
- Quelques سوالات de topologie ، 1958.
- جبر همولوگ (با S. Eilenberg)، پرینستون یونو پرس، 1956 ISBN 978-0-69104991-5 [8]
- Séminaires de l'École normalale supérieure (به نام "Séininaires Cartan")، Sec. ریاضی. IHP ، 1948-1964؛ نیویورک، WABenjamin ed.، 1967.
- Théorie élémentaire des fonctions analytiques ، پاریس، هرمان، 1961 (ترجمه به زبان انگلیسی، آلمانی، ژاپنی، اسپانیایی و روسی).
- Calcul Difrrentiel ، پاریس، هرمان، 1967 (ترجمه به زبان انگلیسی، اسپانیایی و روسی).
- Formes différents ، Paris، Hermann، 1967 (ترجمه به انگلیسی، اسپانیایی و روسی).
- فرم های دیفرانسیل ، Dover 2006
- Œuvres - Collected Works، 3 vols.، ed. رینولد رمرت و ژان پیر سار ، Springer Verlag، Heidelberg، 1967.
- روابط عمومی ادیان و مذاهب ، نوشهتل، 1973.
- تئوری élémentaire فونکس تجزیه و تحلیل مجموعه ای از متغیرهای متغیرهای پویا ، پاریس، هرمان، 1975.
- تئوری ابتدایی توابع تحلیلی یک یا چند متغیر پیچیده ، Dover 1995
- Cours de calcul différentiel ، پاریس، هرمان، 1977.
- Correspondance entre Henri Cartan et André Weil ، Paris، SMF، 2011. [9]
یادداشت ها [ ویرایش ]
- ^ Serre، J.-P. (2009). "هنری پل کارتر" 8 جولای 1904 - 13 اوت 2008 ". خاطرات خاطرات دوستانه انجمن سلطنتی . 55 : 37-44. doi : 10.1098 / rsbm.2009.0005 .
- ^ پرش به بالاب "Décès رقیق mathématicien هانری کارتن" ، فیگارو ، 2008/08/18
- ^ هنری کارتان در پروژه ژنتیک ریاضیات
- ^ کارتان و ایلنبرگ 1956 را ببینید
- ^ اطلاعیه های AMS، جلد. 46 (7)، صفحه 788
- ^ کارتن، هنری. "Problèmes globaux dans la théorie des fonctions analytiques de plusieurs متغیرهای مجتمع." در Proc بین المللی کانگ ریاضی، جلد 1، ص 152-164. 1950
- ^ کارتن، هنری. "مجتمع های متغیرهای مختلفی را در اختیار شما قرار می دهد. در Proc کارآموز ریاضیدانان کنگره ادینبورگ، ص 33-52. 1958
- ^ مک لین، سوندرز (1956). "نقد: جبر همولوگ ، توسط هنری کارتان و ساموئل ایلنبرگ" . بول عامر ریاضی. SOC . 62 (6): 615-624. doi : 10.1090 / S0002-9904-1956-10082-7 .
- ^ فرسان، خاویر (ژوئن 2012). "نقد و بررسی: Correspondance entre Henri Cartan و André Weil edited by Michèle Audin" (PDF) . خبرنامه EMS . ص 58-60.
از ویکیپدیا، دانشنامه آزاد
در جبر، در قضیه جاکوبسن-Bourbaki را یک قضیه استفاده به گسترش است نظریه Galois به پسوند درست است که باید از هم جدا نمی شود. توسط ناتان جاکوبسون ( 1944 ) برای زمینه هایجایگزینی معرفی شد و توسط Jacobson (1947) و Henri Cartan ( 1947 ) که به نتیجه نرسیدن به کار منتشر شده توسط نیکولاس بوربکی بود، به نواحی غیرمنتظره ای گسترش یافت .گسترش نظریه گالویز به فرمت های معمول ، مکاتبات جاکوبسن بوربکی نامیده می شود ، که جایگزین مکاتبات میان برخی از زیرفایل هااز یک میدان و برخی از زیر گروه های گروه Galois توسط مکاتبات بین برخی از حلقه های فرعی تقسیم حلقه و برخی از Subalgebras جبر.
قضیه جاکوبسون-بوربکی، همبستگی متداول Galois را برای زیربناهای گسترش گالوئیز نشان می دهد، و مکاتبات گالوئیز جاکوبسن برای زیربناهای تک تک جدایی ناپذیری از شاخص را بیشتر از 1.
بیانیه [ ویرایش ]
فرض کنید L یک حلقه تقسیم است . قضیه جاکوبسن-بوربکی بیان می کند که یک پیوند طبیعی 1: 1 وجود دارد:
حلقه های بخش K در L مشخصه n (به عبارت دیگر L یک فضای بردار چپ محدود بر K است ).
Unital K- algebras of dimensional finite n (به عنوان فضاهای K- vector) در حلقه اندومورفیسم های گروه افزودنی K وجود دارد .
حلقه زیر بخش و جبهه متناظر مربوط به جایگزین های یکدیگر هستند.
جاکوبسون ( فصل ششم، 1956 ) یک فرمت را برای حلقه های زیرزمینی ارائه داد که ممکن است دارای نام بی نهایت باشد، که مطابق با حلقه های بسته در توپولوژی محدود است.
ساموئل آیلنبرگ (30 سپتامبر 1913 - 30 ژانویه 1998) یک ریاضیدان آمریکایی لهستانی بود که با سوندرز مک لاین تئوری طبقه بندی را تشکیل داد .
زندگی زودهنگام و آموزش [ ویرایش ]
او در ورشو ، پادشاهی لهستان به یک خانواده یهودی متولد شد و در نیویورک ، ایالات متحده آمریکا، جایی که او عمدتا به عنوان استاددانشگاه دانشگاه کلمبیا درگذشت.
او دکترای خود را به دست آورد از دانشگاه ورشو در سال 1936. مشاور کارشناسی وی کارول برسوک بود .
شغل [ ویرایش ]
اصلی کار آیلنبرگ در توپولوژی جبری بود . او در درمان اصطلاحات نظریه هماهنگی با نورمن استینرود (که نام آنها ایزوئل ایلنبرگ-استینرود است ) کار می کند و بر جبر هموژن با سوندرز مک لین کار می کرد . در این فرآیند، ایلنبرگ و مک لین، نظریه مجموعه راایجاد کردند .
Eilenberg عضو بود Bourbaki را ، و با هانری کارتن ، نوشت: 1956 کتاب همانند جبر ، [1] .
بعدها در زندگی او عمدتا در نظریه گروهی کار می کرد، که یکی از بنیانگذاران این حوزه بود. Eilenberg را مغبون (یا تلسکوپ ) ساخت و ساز استفاده از است تلسکوپی لغو ایده را به ماژول های تصویری .
ایلنبرگ به تئوری اتوماتا و نظریه ی ماشین های جبری کمک کرد. به ویژه، او مدل محاسباتی به نام X-machine و یک الگوریتم جدید تجزیه اولیه برای دستگاه های دولتی محدود در ورید نظریه کرون-رودس معرفی کرد .
مجموعه هنری [ ویرایش ]
آیلنبرگ همچنین یکی از مجموعه های برجسته هنر آسیایی بود. مجموعه او عمدتا شامل مجسمه های کوچک و مصنوعات دیگر از هند، اندونزی، نپال، تایلند، کامبوج، سریلانکا و آسیای مرکزی بود. در سالهای 1991-1992، موزه هنر متروپولیتن در نیویورک نمایشگاه از بیش از 400 آیتم را که ایلنبرگ به موزه اهدا کرده است تحت عنوان " هنر لاتوی متعالی: هنر هند و آسیای جنوب شرقی" از مجموعه ساموئل آیلنبرگ برگزار کرد . [2] در همکاری، موزه هنر متروپولیتن به طور قابل ملاحظه ای به اهدای استاد بازدید از ریاضیات دانشگاه ساموئل ایلنبرگ در دانشگاه کلمبیا اهدا شد. [3]
نشریات منتخب [ ویرایش ]
- ایلنبرگ، ساموئل (1974). خودکار زبان و ماشین آلات، جلد یک . ISBN 0-12-234001-9.
- ایلنبرگ، ساموئل (1976). خودکار زبان و ماشین آلات، جلد B . ISBN 0-12-234002-7.
- آیلنبرگ، ساموئل؛ گانه، تودور (1957). "در گروه Lusternik-Schnirelmann از گروه انتزاعی". سالانه ریاضیات . سری دوم 65 (3): 517-518. JSTOR 1970062 . MR 0085510 .
- آیلنبرگ، ساموئل؛ مک لین، سوندرز (1945). "روابط همخوانی و گروه های homotopy از فضاهای". سالانه ریاضیات . 46 : 480-509. doi : 10.2307 / 1969165 .
- آیلنبرگ، ساموئل؛ مک لین، سوندرز (1950). "روابط همخوانی و گروه های homotopy از فضاهای. II". سالانه ریاضیات . 51 : 514-533. doi : 10.2307 / 1969365 .
- آیلنبرگ، ساموئل؛ مور، جان C. (1962)، "محدودیت ها و توالی طیفی"، توپولوژی ، 1 (1): 1-23، doi : 10.1016 / 0040-9383 (62) 90093-9 ، ISSN 0040-9383
- آیلنبرگ، ساموئل؛ نینو، ایوان (1944). "قضیه اساسی جبر" برای quaternions ". بولتن انجمن ریاضی آمریکا . 50 (4): 246-248. doi : 10.1090 / s0002-9904-1944-08125-1 . MR 0009588 .
- آیلنبرگ، ساموئل ؛ Steenrod، Norman E. (1945). "رویکرد axiomatic به نظریه هماهنگی" . مجموعه مقالات آکادمی ملی علوم ایالات متحده آمریکا . 31 (4): 117-120. doi : 10.1073 / pnas.31.4.117 . PMC 1078770 . PMID 16578143 .
- ساموئل آیلنبرگ و نورمن استینرد (1952)، بنیان های توپولوژی جبری ، دانشگاه پرینستون مطبوعات ، پرینستون، نیوجرسی. xv + 328 pp. [4]
همچنین نگاه کنید به [ ویرایش ]
مشخصات وب
 در این وبلاگ به ریاضیات و کاربردهای آن و تحقیقات در آنها پرداخته می شود. مطالب در این وبلاگ ترجمه سطحی و اولیه است و کامل نیست.در صورتی سوال یا نظری در زمینه ریاضیات دارید مطرح نمایید .در صورت امکان به آن می پردازم. من دوست دارم برای یافتن پاسخ به سوالات و حل پروژه های علمی با دیگران همکاری نمایم.در صورتی که شما هم بامن هم عقیده هستید با من تماس بگیرید.
در این وبلاگ به ریاضیات و کاربردهای آن و تحقیقات در آنها پرداخته می شود. مطالب در این وبلاگ ترجمه سطحی و اولیه است و کامل نیست.در صورتی سوال یا نظری در زمینه ریاضیات دارید مطرح نمایید .در صورت امکان به آن می پردازم. من دوست دارم برای یافتن پاسخ به سوالات و حل پروژه های علمی با دیگران همکاری نمایم.در صورتی که شما هم بامن هم عقیده هستید با من تماس بگیرید.09132003030
موضوعات وب
- نظریه طیف گراف
- پرواز
- هندسه
- هسته ای
- ترکببات
- نمایش گروه
- سیستم های دینامیکی
- نظریه کد گذاری
- ریاضی فازی
- جبر پیشرفته
- توپولوژی
- معادلات دیفرانسیل
- مقاله ها
- سیستم عصبی
- آنالیز عددی
- آنالیزریاضی و آنالیز حقیقی
- توابع مختلط و کاربردها
- نظریه اعداد
- برنامه ریزی خطی و غیر خطی
- حل عددی معادلات دیفرانسیل
- نظریه مجموعه ها
- جبرخطی و جبرخطی عددی
- اقتصاد
- تاریخ ریاضی
- انسان شناسی وفلسفه ریاضی
- توپولوژی جبری
- هندسه جبری
- هندسه ریمانی و هندسه هذلوی
- بازی
- نقشه برداری دریایی
- گراف
- آمار غیرپارامتری
- نجوم
- منیفولد دیفرانسیل
- نظریه گروه
- نظریه حلقه
- نظریه مدول ها
- آمار و احتمال
- ریاضی 2
- فیزیک -ریاضی
- تحقیق
- ریاضی مهندسی
- درس ترمودینامیک و مکانیک آماری
- مکانیک تحلیلی
- برق یا فیزیک 2
- فیزیک مدرن
- کوانتم
- نسبیت
پیوندها
پیوندهای روزانه
آرشیو وب
- دی ۱۴۰۴
- آذر ۱۴۰۴
- آبان ۱۴۰۴
- شهریور ۱۴۰۴
- مرداد ۱۴۰۴
- خرداد ۱۴۰۴
- اردیبهشت ۱۴۰۴
- بهمن ۱۴۰۳
- دی ۱۴۰۳
- آذر ۱۴۰۳
- آبان ۱۴۰۳
- مهر ۱۴۰۳
- خرداد ۱۴۰۳
- اردیبهشت ۱۴۰۳
- فروردین ۱۴۰۳
- اسفند ۱۴۰۲
- بهمن ۱۴۰۲
- دی ۱۴۰۲
- آذر ۱۴۰۲
- آبان ۱۴۰۲
- مهر ۱۴۰۲
- تیر ۱۴۰۲
- خرداد ۱۴۰۲
- اردیبهشت ۱۴۰۲
- فروردین ۱۴۰۲
- اسفند ۱۴۰۱
- بهمن ۱۴۰۱
- دی ۱۴۰۱
- آبان ۱۴۰۱
- مهر ۱۴۰۱
- شهریور ۱۴۰۱
- مرداد ۱۴۰۱
- تیر ۱۴۰۱
- خرداد ۱۴۰۱
- اردیبهشت ۱۴۰۱
- فروردین ۱۴۰۱
- آرشيو













![\ mathbf {x} _ {n + 1} = \ mathbf {x} _ {n} - [\ mathbf {H} f (\ mathbf {x} _ {n})] ^ {-1} \ nabla f \ mathbf {x} _ {n})، \ n \ geq 0.](https://wikimedia.org/api/rest_v1/media/math/render/svg/75802c220f63e636fda641fbe2c953ed656a2ee2)
![\ mathbf {x} _ {n + 1} = \ mathbf {x} _ {n} - \ gamma [\ mathbf {H} f (\ mathbf {x} _ {n})] ^ {- 1} \ nabla f (\ mathbf {x} _ {n}).](https://wikimedia.org/api/rest_v1/media/math/render/svg/d8b266ce1ac150b43acb59eca9abf45fc08a33db)
![[\ mathbf {H} f (\ mathbf {x} _ {n})] \ mathbf {\ Delta x} = - \ nabla f (\ mathbf {x} _ {n})](https://wikimedia.org/api/rest_v1/media/math/render/svg/c19002921fdd62924a8d1b07f3a1e196d6f3e3ec)




















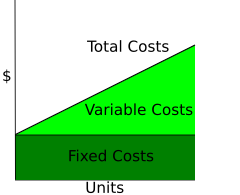

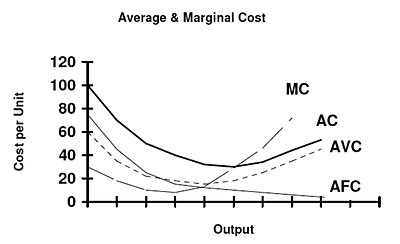

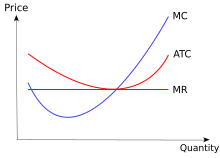























![{\ displaystyle e ^ {\ pi} = [23؛ 7،9،3،1،1،591،2،9،1،2،34،1،16،1،30،1،1،4،1،2،108 ، 2،2،1،3،1،7،1،2،2،2،1،2،3،2،166،1،2،1،4،8،10،1،1،7،1،2 ، 3،566،1،2،3،3،1،20،1،2،19،1،3،2،1،2،13،2،2،11، ...]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/372cedf7e3241e2517c20b27580b84e05c82a828)




















![{\ displaystyle f * g = {\ begin {cases} f (2t) و t \ in \ left [0، {\ tfrac {1} {2}} \ right] \\ g (2t-1) سمت چپ [{\ tfrac {1} {2}}، 1 \ سمت راست] \ end {cases}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/50ab490862e065e07d5b7c9d2f48c69e8fa7a766)
![{\ displaystyle (f + g) (t_ {1}، t_ {2}، \ ldots، t_ {n}) = {\ begin {cases} f (2t_ {1}، t_ {2}، \ ldots، t_ {n}) و t_ {1} \ in \ left [0، {\ tfrac {1} {2}} \ right] \\ g (2t_ {1} -1، t_ {2}، \ ldots، t_ {n }) & t_ {1} \ in \ left [{\ tfrac {1} {2}}، 1 \ right] \ end {cases}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/d292ba059108f5c62b4abe9edb1bb2776cb22cf8)



