1-انتگرال مختلط
قضیه کوشی
3.1 تعریف
3.1.1 همبند
یک منطقه همبند ، منطقه ای است که هر دو نقطه در آن را می توان با یک منحنی که به طور کامل در منطقه قرار دارد به هم متصل کرد.
3.1.2 منطقه به سادگی همبند
منحنی که از خود عبور نمی کند منحنی بسته ساده نامیده می شود. ناحیه ای که در آن هر منحنی بسته در آن تنها نقاطی از ناحیه را در بر می گیرد، منطقه ای به سادگی همبند نامیده می شود.
3.1.3 انتگرال کانتور
انتگرال در امتداد یک منحنی بسته ساده را انتگرال کانتور می نامند.
3.1.4 قضیه انتگرال کوشی
اگر تابع f(z) تحلیلی باشد و مشتق آن f 0 (z) پیوسته باشد
آر
تمام نقاط داخل و روی یک منحنی بسته ساده c، سپس c f(z)dz = 0:
3.1.5 فرمول انتگرال کوشی
اگر f(z) در داخل و روی یک منحنی بسته c از یک ناحیه R که به سادگی متصل شده است تحلیلی باشد و اگر a هر نقطه ای با c باشد، آنگاه
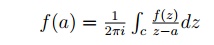
انتگرال حول c در جهت مثبت گرفته می شود.
3.1.6 فرمول انتگرال کوشی برای مشتق
اگر تابع f(z) درون و روی یک منحنی بسته ساده c تحلیلی باشد و a هر نقطه ای باشد که در آن قرار دارد، آنگاه
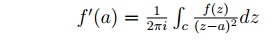
3.2 نمونه های کار شده

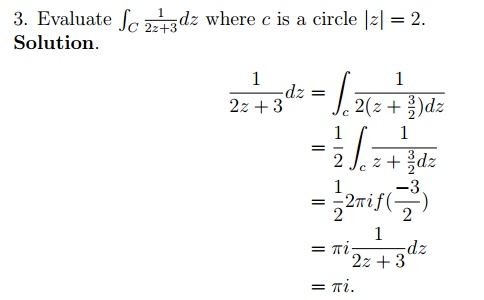

3.3 مسائل
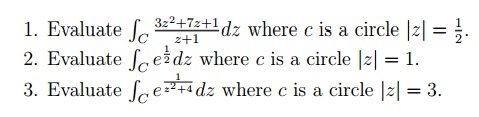
4 گسترش سری تیلور و لورن.
4.1 سری تیلور.
یک تابع f(z)، تحلیلی در داخل دایره C با مرکز a، می تواند در سری بسط داده شود
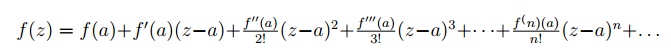
4.2 سری Laurent.
اجازه دهید C 1 ; C 2 دو دایره متحدالمرکز jz aj = R 1 و jz aj = R 2 باشد که در آن R 2 < R 1 : فرض کنید f(z) در C 1 و C 2 و در ناحیه حلقوی R بین آنها تحلیلی باشد. سپس، برای هر نقطه z در R،
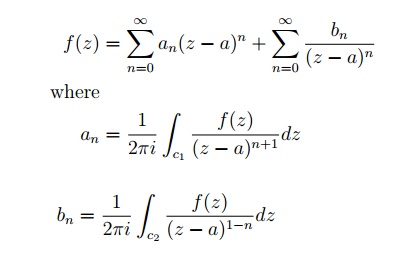
جایی که انتگرال ها در خلاف جهت عقربه های ساعت گرفته می شوند.
4.3 نمونه های کار شده
1. e z را در یک سری تیلور حدود z = 0 بسط دهید
راه حل.

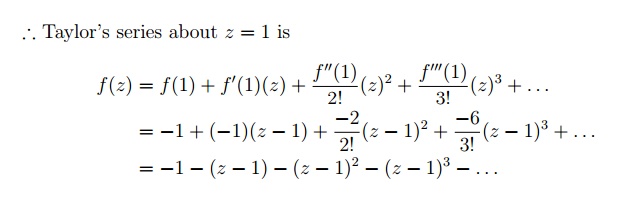

منبع
https://www.brainkart.com/article/Complex-Integration_6461/
4.4 مشکلات آموزشی
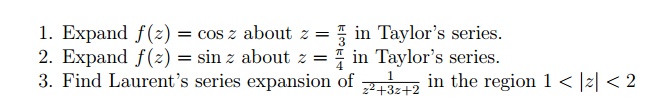
5 تکینگی ها
5.1 تعریف
5.1.2 صفرهای یک تابع تحلیلی:
اگر یک تابع f(z) تحلیلی در یک منطقه R در نقطه z = z 0 در R صفر باشد، z 0 را صفر از f(z) می گویند.
5.1.3 صفر ساده:
اگر f(z 0 ) = 0 و f 0 (z 0 ) 6 = 0، z = z 0 یک صفر ساده از f(z) یا یک صفر از مرتبه اول نامیده می شود.
5.1.4 صفر از ترتیب n:
اگر f(z) را بتوان به صورت f(z) = (zz 0 ) m (z) که (z) تحلیلی و (z 0 ) 6 بیان کرد، یک تابع تحلیلی f(z) دارای صفر مرتبه n است. = 0
5.1.5 امتیازهای مفرد:
نقطه z = z 0 که در آن تابع f(z) تحلیلی نباشد نقطه منفرد نامیده می شود.
5.1.6 کل عملکرد
تابع f(z) که در همه جای صفحه نیت تحلیلی است یک تابع کامل نامیده می شود.
5.1.7 تابع مرومورفیک
تابع f(z) که در همه جای صفحه نیت به جز در تعداد قطبهای nیت تحلیلی است تابع مرومورفیک نامیده می شود.
5.2 انواع تکینگی ها
5.2.1. تکینگی جدا شده
یک نقطه z = z 0 می گویند تکینگی جدا شده از f(z) اگر
1. f(z) در z = z 0 تحلیلی نیست
2. همسایگی z = z 0 وجود دارد که هیچ تکینگی دیگری ندارد.
5.2.2. تکینگی قابل جابجایی:
اگر قسمت اصلی f(z) در بسط سری Laurent از f(z) حول نقطه z 0 صفر باشد، نقطه z = z 0 تکینگی قابل جابجایی نامیده می شود.
5.2.3. قطب:
اگر بتوانیم یک عدد صحیح مثبت n را طوری بیابیم که z!a (za) n f(z) 6= 0 باشد، آنگاه z = a قطبی از مرتبه n برای f(z) نامیده می شود.
5.2.4. تکینگی اساسی:
اگر قسمت اصلی f(z) در بسط سری Laurent از f(z) در مورد نقطه z 0 به صورت عددی دارای عبارات غیر صفر باشد، نقطه z = z 0 را تکینگی اساسی می گویند.
5.5.3 نمونه های کار شده

تابع f(z) در z = 0 تعریف نمی شود.
با قانون L'Hospital
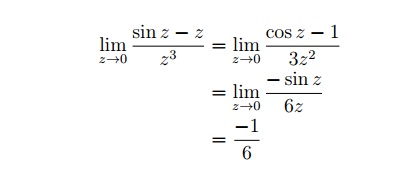
از آنجایی که حد وجود دارد و nite است، تکینگی در z = 0 یک تکینگی قابل جابجایی است.
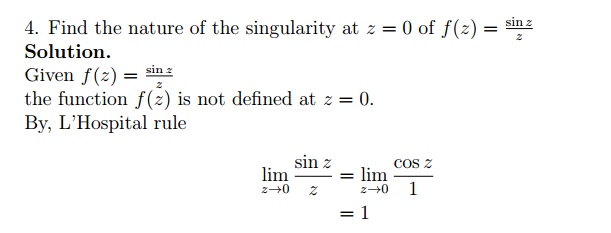
از آنجایی که حد وجود دارد و nite است، تکینگی در z = 0 یک تکینگی قابل جابجایی است.

5.5.4 مشکلات آموزشی
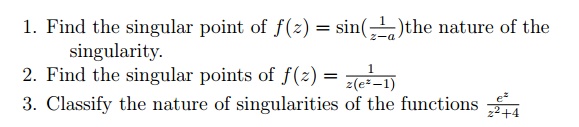
6 باقیمانده
6.1 تعاریف:
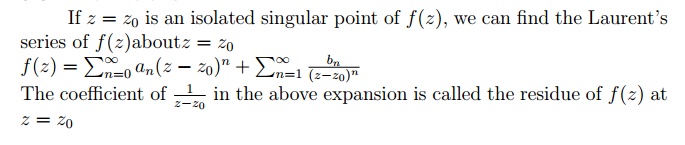
 در این وبلاگ به ریاضیات و کاربردهای آن و تحقیقات در آنها پرداخته می شود. مطالب در این وبلاگ ترجمه سطحی و اولیه است و کامل نیست.در صورتی سوال یا نظری در زمینه ریاضیات دارید مطرح نمایید .در صورت امکان به آن می پردازم. من دوست دارم برای یافتن پاسخ به سوالات و حل پروژه های علمی با دیگران همکاری نمایم.در صورتی که شما هم بامن هم عقیده هستید با من تماس بگیرید.
در این وبلاگ به ریاضیات و کاربردهای آن و تحقیقات در آنها پرداخته می شود. مطالب در این وبلاگ ترجمه سطحی و اولیه است و کامل نیست.در صورتی سوال یا نظری در زمینه ریاضیات دارید مطرح نمایید .در صورت امکان به آن می پردازم. من دوست دارم برای یافتن پاسخ به سوالات و حل پروژه های علمی با دیگران همکاری نمایم.در صورتی که شما هم بامن هم عقیده هستید با من تماس بگیرید.