قضیه تیچمارش [ ویرایش ]

قضیه Titchmarsh (به نام EC Titchmarsh که آن را در کار خود در سال 1937 گنجانده است) رابطه دقیق بین مقادیر مرزی توابع هولومورفیک را در نیمه صفحه فوقانی و تبدیل هیلبرت ایجاد می کند. [33] این شرایط لازم و کافی را برای یک تابع قابل جمع شدن مربع با ارزش پیچیده F ( x ) در خط واقعی فراهم می کند تا مقدار مرزی یک تابع در فضای هاردی H 2 ( U ) توابع هولوومرف در نیمه بالایی باشد هواپیما U .

این قضیه بیان می کند که شرایط زیر برای یک تابع مجتمع مربع با ارزش پیچیده است {\ displaystyle F: \ mathbb {R} \ به \ mathbb {C}} معادل هستند:

  • F ( x ) حد z → x یک تابع holomorphic F ( z ) در نیمه صفحه فوقانی است به طوری که

    {\ displaystyle \ int _ {- \ infty} ^ {\ infty} | F (x + i \، y) | ^ {2} \؛ \ mathrm {d} x <K}

  • قسمتهای واقعی و خیالی F ( x ) تبدیل هیلبرت به یکدیگر هستند.
  • تبدیل فوریه {\ mathcal {F}} (F) (x)برای x <0 محو می شود .

نتیجه ضعیف تری برای توابع کلاس L p برای p > 1 صادق است . [34] به طور خاص ، اگر F ( z ) یک تابع هولومورفیک باشد به گونه ای که

 

 

{\ displaystyle \ int _ {- \ infty} ^ {\ infty} | F (x + i \، y) | ^ {p} \؛ \ mathrm {d} x <K}

 

برای همه y ، یک تابع با ارزش پیچیده F ( x ) در وجود دارد{\ displaystyle L ^ {p} (\ mathbb {R})}به طوری که F ( x + iy ) → F ( x ) در هنجار L p به عنوان y → 0 (و همچنین تقریباً در همه جا به صورت نقطه ای نگه داشته می شود ). علاوه بر این،

 

{\ displaystyle F (x) = f (x) -i \ ، g (x)}

 

که در آن f یک تابع با ارزش واقعی است{\ displaystyle L ^ {p} (\ mathbb {R})}و g تبدیل هیلبرت (از کلاس L p ) f است .

این در مورد p = 1 درست نیست . در واقع ، تبدیل هیلبرت از یک تابع L 1 f نیازی به میانگین در یک تابع L 1 دیگر ندارد. با این وجود ، [35] تبدیل هیلبرت f تقریباً در همه جا به یک تابع محدود g تبدیل می شود به گونه ای که

{\ displaystyle \ int _ {- \ infty} ^ {\ infty} {\ frac {| g (x) | ^ {p}} {1 + x ^ {2}}} \؛ \ mathrm {d} x < \ بی فایده}

 

این نتیجه مستقیماً مشابه آندری کلموگروف برای عملکردهای هاردی در دیسک است. [36] اگرچه معمولاً قضیه Titchmarsh نامیده می شود ، اما نتیجه کار بسیاری از افراد دیگر ، از جمله هاردی ، پالی و وینر است (به قضیه پالی- وینر مراجعه کنید ) ، و همچنین کارهای Riesz ، Hille و Tamarkin [37]

مسئله ریمان-هیلبرت [ ویرایش ]

یک فرم از مشکل ریمان-هیلبرت به دنبال شناسایی جفت از توابع F + و F - به طوری که F + است هولومورفیک در قسمت نیمه هواپیما و F - هولومورفیک در پایین نیمه هواپیما، است به طوری که برای X در امتداد واقعی محور،

{\ displaystyle F _ {+} (x) -F _ {-} (x) = f (x)}

 

که در آن f ( x ) برخی از عملکردهای دارای ارزش واقعی است{\ displaystyle x \ in \ mathbb {R}}. سمت چپ این معادله را می توان به عنوان تفاوت محدوده های F ± از نیم صفحه مناسب ، یا به عنوان یک توزیع فوق عملکرد درک کرد . دو عملکرد این فرم راه حل مسئله ریمان-هیلبرت است.

بعبارت دیگر، اگر F ± حل مشکل ریمان-هیلبرت

{\ displaystyle f (x) = F _ {+} (x) -F _ {-} (x)}

سپس تبدیل هیلبرت f ( x ) توسط [38] داده می شود

{\ displaystyle H (f) (x) = - i {\ bigl (} F _ {+} (x) + F _ {-} (x) {\ bigr)}.}

هیلبرت روی دایره تغییر شکل می دهد [ ویرایش ]

همچنین نگاه کنید به: Hardy space

برای یک تابع تناوبی F هیلبرت دایره تبدیل تعریف شده است:

 

{\ displaystyle {\ tilde {f}} (x) \ triangleq {\ frac {1} {2 \ pi}} \ operatorname {pv} \ int _ {0} ^ {2 \ pi} f (t) \، \ cot \ چپ ({\ frac {xt} {2}} \ راست) \ ، \ mathrm {d} t}

تبدیل هیلبرت دایره ای در توصیف فضای هاردی و در مطالعه عملکرد مزدوج در سری فوریه استفاده می شود. هسته ،

{\ displaystyle \ cot \ left ({\ frac {xt} {2}} \ right)}

به عنوان هسته هیلبرت شناخته می شود ، از آنجا که در ابتدا شکل هیلبرت مورد بررسی قرار گرفت. [8]

 

هسته هیلبرت (برای تبدیل دایره ای هیلبرت) را می توان با ایجاد دوره ای 1 ⁄ x هسته کوشی بدست آورد . دقیق تر ، برای x ≠ 0

{\ displaystyle {\ frac {1} {\، 2 \،}} \ cot \ left ({\ frac {x} {2}} \ right) = {\ frac {1} {x}} + \ sum _ {n = 1} ^ {\ نادرست} \ چپ ({\ frac {1} {x + 2n \ pi}} + {\ frac {1} {\، x-2n \ pi \،}} \ راست)}

 

بسیاری از نتایج در مورد تبدیل دایره ای هیلبرت ممکن است از نتایج مربوط به تبدیل هیلبرت از این مکاتبات حاصل شود.

اتصال مستقیم دیگر با تبدیل Cayley C ( x ) = ( x - i ) / ( x + i ) فراهم می شود ، که خط واقعی را به دایره و نیمه صفحه بالایی را به دیسک واحد منتقل می کند. این یک نقشه واحد را القا می کند

{\ displaystyle U \، f (x) = {\ frac {1} {(x + i) \، {\ sqrt {\ pi}}}} \، f \ چپ (C \ چپ (x \ راست) \ درست)}

 

از L 2 ( T ) بر روی{\ displaystyle L ^ {2} (\ mathbb {R}).}اپراتور U فضای Hardy H 2 ( T ) را به فضای Hardy حمل می کند{\ displaystyle H ^ {2} (\ mathbb {R})}. [39]

تبدیل هیلبرت در پردازش سیگنال [ ویرایش ]

قضیه بدروسیان [ ویرایش ]

قضیه Bedrosian بیان می دارد که تبدیل هیلبرت محصول سیگنال کم گذر و سیگنال بالا با طیفهای غیر همپوشانی توسط محصول سیگنال کم گذر و تبدیل هیلبرت سیگنال عبور بالا ارائه می شود ، یا

 

 

{\ displaystyle \ operatorname {H} \ left (f _ {\ text {LP}} (t) \ cdot f _ {\ text {HP}} (t) \ right) = f _ {\ text {LP}} (t) \ cdot \ operatorname {H} \ چپ (f _ {\ text {HP}} (t) \ راست) ،}

 

جایی که f LP و f HP به ترتیب سیگنال های کم و زیاد هستند. [40] به دسته ای از سیگنال های ارتباطی که این امر به آنها اعمال می شود ، مدل سیگنال باند باریک گفته می شود. عضو آن دسته مدولاسیون دامنه یک "حامل" سینوسی با فرکانس بالا است:

 

{\ displaystyle u (t) = u_ {m} (t) \ cdot \ cos (\ امگا t + \ phi) ،}

 

جایی که u m ( t ) شکل موج "پیام" پهنای باند باریک است ، مانند صدا یا موسیقی. سپس با قضیه Bedrosian: [41]

{\ displaystyle \ operatorname {H} (u) (t) = u_ {m} (t) \ cdot \ sin (\ امگا t + \ phi).}

 

نمایش تحلیلی [ ویرایش ]

مقاله اصلی: سیگنال تحلیلی

نوع خاصی از تابع مزدوج است :

{\ displaystyle u_ {a} (t) \ triangleq u (t) + i \ cdot H (u) (t)،}

 

شناخته شده به عنوان نمایندگی تحلیلی از{\ displaystyle u (t).} این نام قابل انعطاف پذیری ریاضی آن است ، که بیشتر به فرمول اویلر مربوط می شود . با استفاده از قضیه Bedrosian در مدل باریک ، نمایش تحلیلی این است : [42]

{\ displaystyle {\ start {تراز شده} u_ {a} (t) & = u_ {m} (t) \ cdot \ cos (\ امگا t + \ phi) + i \ cdot u_ {m} (t) \ cdot \ sin (\ امگا t + \ phi) \\ & = u_ {m} (t) \ cdot \ چپ [\ cos (\ امگا t + \ phi) + i \ cdot \ sin (\ امگا t + \ phi) \ راست] \ \ & = u_ {m} (t) \ cdot e ^ {i (\ امگا t + \ phi)}. \ ، \ پایان {تراز شده}}}

 

 

 

 

( معادله 1 )

یک ویژگی تبدیل فوریه نشان می دهد که این عملیات هدرودین پیچیده می تواند تمام اجزای فرکانس منفی u m ( t ) را به بالای 0 هرتز تغییر دهد. در آن صورت ، قسمت خیالی نتیجه ، تبدیل هیلبرت قسمت واقعی است. این یک روش غیر مستقیم برای تولید تحولات هیلبرت است.

مدولاسیون زاویه (فاز / فرکانس) [ ویرایش ]

فرم: [43]

 

{\ displaystyle u (t) = A \ cdot \ cos (\ امگا t + \ phi _ {m} (t))}}

 

مدولاسیون زاویه ای نامیده می شود که شامل هر دو مدولاسیون فاز و مدولاسیون فرکانس می باشد. فرکانس لحظه است \ امگا + \ phi _ {m} ^ {\ prime} (t).  برای ω کاملاً بزرگ ، در مقایسه با\ phi _ {m} ^ {\ prime}:

{\ displaystyle \ operatorname {H} (u) (t) \ تقریبی A \ cdot \ sin (\ امگا t + \ phi _ {m} (t))}

و:

{\ displaystyle u_ {a} (t) \ تقریبی A \ cdot e ^ {i (\ امگا t + \ phi _ {m} (t))}}.}

مدولاسیون باند کناری (SSB) [ ویرایش ]

مقاله اصلی: مدولاسیون باند یک طرفه

وقتی تو م ( تی ) در  Eq.1 همچنین یک نمایندگی تحلیلی (یک شکل موج پیام)، این است که:

{\ displaystyle u_ {m} (t) = m (t) + i \ cdot {\ widehat {m}} (t)}

نتیجه مدولاسیون باند یک طرفه است :

{\ displaystyle u_ {a} (t) = (m (t) + i \ cdot {\ widehat {m}} (t)) \ cdot e ^ {i (\ omega t + \ phi)}}}

مولفه منتقل شده آن: [44] [45]

{\ displaystyle {\ start {تراز شده} u (t) & = \ operatorname {Re} \ {u_ {a} (t) \} \\ & = m (t) \ cdot \ cos (\ امگا t + \ phi) - {\ widehat {m}} (t) \ cdot \ sin (\ امگا t + \ phi) \ پایان {تراز شده}}}

 

علیت [ ویرایش ]

کارکرد {\ displaystyle h (t) = 1 / (\ pi t)} دو چالش برای اجرای عملی به عنوان تجمع ارائه می دهد:

  • مدت زمان آن بی نهایت است ( پشتیبانی فنی بی نهایت ). به جای آن باید از تقریب طول محدود استفاده شود. اما پنجره شدن طول ، دامنه فرکانس موثر تبدیل را نیز کاهش می دهد. هرچه پنجره کوتاه تر باشد ، تلفات در فرکانس های پایین و زیاد بیشتر خواهد بود. همچنین به فیلتر کوادراتور مراجعه کنید .
  • این یک فیلتر غیر علی است . بنابراین یک نسخه با تأخیر ،{\ displaystyle h (t- \ tau) ،}مورد نیاز است. خروجی مربوطه متعاقباً توسط به تأخیر می افتد\ تاو هنگام ایجاد قسمت خیالی یک سیگنال تحلیلی ، منبع (قسمت واقعی) باید با مقدار معادل آن به تأخیر بیفتد.

تبدیل گسسته هیلبرت [ ویرایش ]

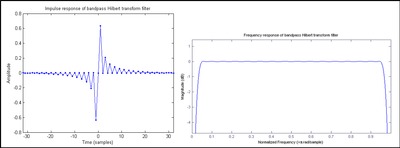
شکل 1 : فیلترهایی که پاسخ فرکانس آنها محدود به حدود 95٪ فرکانس Nyquist است

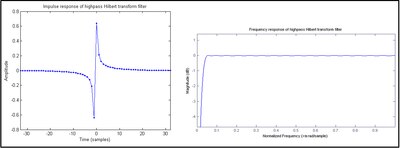
شکل 2 : فیلتر تبدیل هیلبرت با پاسخ فرکانس گذر زیاد

شکل 3 .

شکل 4 . تبدیل هیلبرت از COS ( ωt ) است گناه ( ωt ) . این شکل نشان می دهد sin (ωt) و دو تبدیل هیلبرت تقریبی محاسبه شده توسط عملکرد کتابخانه MATLAB ، hilbert ()

شکل 5 . هیلبرت گسسته یک تابع کسینوس را با استفاده از تجزیه قطعه قطعه تبدیل می کند

برای یک عملکرد گسسته ، تو [n]، با تبدیل فوریه گسسته (DTFT) ،{\ displaystyle U (\ امگا)}، و تبدیل گسسته هیلبرت{\ hat {u}} [n]، DTFT از{\ hat {u}} [n]در منطقه - π <ω < π توسط:

{\ displaystyle \ operatorname {DTFT} ({\ hat {u}}) = U (\ omega) \ cdot (-i \ cdot \ operatorname {sgn} (\ امگا)).}

 

معکوس DTFT ، با استفاده از قضیه جمع آوری ، عبارت است از: [46]

{\ displaystyle {\ start {تراز شده} {\ کلاه {u}} [n] & = {\ scriptstyle \ mathrm {DTFT} ^ {- 1}} (U (\ omega)) \ * \ {\ scriptstyle \ mathrm {DTFT} ^ {- 1}} (- i \ cdot \ operatorname {sgn} (\ امگا)) \\ & = u [n] \ * \ {\ frac {1} {2 \ pi}} \ int _ {- \ pi} ^ {\ pi} (- i \ cdot \ operatorname {sgn} (\ omega)) \ cdot e ^ {i \ omega n} \، \ mathrm {d} \ omega \\ & = u [ n] \ * \ \ underbrace {{\ frac {1} {2 \ pi}} \ left [\ int _ {- \ pi} ^ {0} i \ cdot e ^ {i \ omega n} \، \ mathrm {d} \ امگا - \ int _ {0} ^ {\ pi} i \ cdot e ^ {i \ omega n} \، \ mathrm {d} \ امگا \ راست]} _ {h [n]} ، \ پایان {تراز شده}}}

جایی که

{\ displaystyle h [n] \ \ triangleq \ {\ start {cases} 0، & {\ text {for}} n {\ text {even}} \\ {\ frac {2} {\ pi n}} & {\ text {for}} n {\ text {odd}} ، \ end {موارد}}}

که یک پاسخ تکانه بی نهایت است (IIR). هنگامی که ترکیب به صورت عددی انجام می شود ، همانطور که در شکل 1 نشان داده شده است ، تقریب FIR برای h [ n ] جایگزین می شود . یک فیلتر FIR با تعداد عجیب ضرایب ضد متقارن نوع III نام دارد که ذاتاً پاسخهایی با اندازه صفر در فرکانسهای 0 و Nyquist از خود نشان می دهد ، در نتیجه در این حالت به شکل فیلتر باند عبور می شود. یک طرح نوع IV (تعداد زوج ضرایب ضد متقارن) در شکل 2 نشان داده شده است . از آنجا که میزان پاسخ در فرکانس Nyquist کاهش نمی یابد ، تقریباً یک ترانسفورماتور هیلبرت ایده آل کمی بهتر از فیلتر عجیب و غریب است. با این حال

  • یک توالی معمولی (یعنی به درستی فیلتر شده و نمونه برداری شده) u [ n ] هیچ اجزای مفیدی در فرکانس Nyquist ندارد.
  • پاسخ ضربه نوع IV نیاز به یک 1 / 2 تغییر نمونه در ساعت [ N ] دنباله. همانطور که در شکل 2 دیده می شود ، ضرایب با ارزش صفر غیر صفر می شوند . بنابراین یک طراحی نوع III دو برابر کارآمدتر از نوع IV است.
  • تأخیر گروهی در طراحی نوع III تعداد عددی صحیح است که هم ترازی را تسهیل می کند {\ hat {u}} [n] با تو [n] ،برای ایجاد یک سیگنال تحلیلی . تأخیر گروهی نوع IV بین دو نمونه به نصف رسیده است.

MATLAB تابع، هیلبرت (U، N) ، [47] convolves AU [n] را ترتیب با مجموع تناوبی : [A]

{\ displaystyle h_ {N} [n] \ \ triangleq \ sum _ {m = - \ infty} ^ {\ infty} h [n-mN]}   [B] [C]

و یک چرخه ( N نمونه) از نتیجه دوره ای را در قسمت خیالی یک دنباله خروجی با ارزش پیچیده برمی گرداند . ترکیب در دامنه فرکانس به عنوان محصول آرایه اجرا می شود {\ displaystyle {\ scriptstyle \ mathrm {DFT}} \ چپ (تو [n] \ راست)}  با نمونه هایی از توزیع - i sgn ( ω ) (که اجزای واقعی و خیالی آنها فقط 0 یا  1 ± هستند ). شکل 3 نیمه سیکل h N [ n ] را با یک قسمت طول معادل h [ n ] مقایسه می کند . با تقریب FIR برای{\ displaystyle h [n]،} نشان داده شده توسط {\ tilde {h}} [n] ، جایگزین کردن {\ displaystyle {\ scriptstyle \ mathrm {DFT}} \ چپ ({\ tilde {h}} [n] \ سمت راست)}برای نمونه های - i sgn ( ω ) منجر به یک نسخه FIR از ترکیب می شود.

قسمت واقعی توالی خروجی توالی ورودی اصلی است ، به طوری که خروجی پیچیده نمایشی تحلیلی از u [ n ] است . وقتی ورودی بخشی از کسینوس خالص باشد ، ترکیب حاصل از دو مقدار مختلف N در شکل 4 (نمودارهای قرمز و آبی) به تصویر کشیده شده است . اثرات لبه مانع از آن می شود که یک عملکرد سینوسی خالص باشد (طرح سبز). از آنجا که h N [ n ] یک دنباله FIR نیست ، میزان نظری اثرات کل توالی خروجی است. اما تفاوت ها با عملکرد سینوسی با فاصله از لبه ها کاهش می یابد. پارامتر Nطول توالی خروجی است. اگر از طول توالی ورودی بیشتر باشد ، ورودی با افزودن عناصر با ارزش صفر اصلاح می شود. در بیشتر موارد ، این میزان اختلافات را کاهش می دهد. اما مدت زمان آنها تحت تأثیر افزایش و سقوط ذاتی پاسخ تکانه h [ n ] است .

قدردانی از اثرات لبه زمانی مهم است که از روشی به نام overlap-save برای انجام کانولوشن در یک توالی طولانی u [ n ] استفاده شود. بخشهای طول N با عملکرد دوره ای ترکیب می شوند:

{\ displaystyle {\ tilde {h}} _ {N} [n] \ \ triangleq \ sum _ {m = - \ infty} ^ {\ infty} {\ tilde {h}} [n-mN].}

وقتی مدت مقادیر غیر صفر از {\ displaystyle {\ tilde {h}} [n]} است {\ displaystyle M <N ،}توالی خروجی شامل N - M + 1 نمونه از {\ کلاه {u}}. خروجی های M - 1 از هر بلوک N دور ریخته می شوندو بلوک های ورودی برای جلوگیری از ایجاد شکاف با آن مقدار همپوشانی دارند.

شکل 5 مثالی از هر دو تابع IIR hilbert (·) و تقریب FIR است. در مثال ، یک تابع سینوسی با محاسبه تبدیل گسسته هیلبرت از یک تابع کسینوس ایجاد می شود ، که در چهار بخش همپوشانی پردازش شده و دوباره به هم متصل می شود. همانطور که نتیجه FIR (آبی) نشان می دهد ، اعوجاج های آشکار در نتیجه IIR (قرمز) ناشی از تفاوت بین h [ n ] و h N [ n ] نیست (سبز و قرمز در شکل 3 ). واقعیت مخروطی بودن h N [ n ] ( پنجره دار)) در واقع در این زمینه مفید است. مشکل واقعی این است که به اندازه کافی پنجره ندارد. به طور موثر ، M = N ، در حالی که روش همپوشانی صرفه جویی به M < N نیاز دارد .

تبدیل هیلبرت نظریه اعداد [ ویرایش ]

عدد تئوری تبدیل هیلبرت یک پسوند [50] تبدیل گسسته هیلبرت به مدول اعداد صحیح یک عدد اول مناسب است. در این امر از تعمیم تبدیل فوریه گسسته به تبدیل نظری عدد پیروی می کند . از تبدیل تئوریک هیلبرت برای تولید مجموعه ای از توالی های گسسته متعامد می توان استفاده کرد. [51]

همچنین به 

https://en.wikipedia.org/wiki/Hilbert_transform