برآورد فاصله [ ویرایش ]
مقاله اصلی: برآورد فاصله
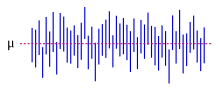
فواصل اطمینان : خط قرمز برای میانگین در این مثال مقدار واقعی است ، خطوط آبی فواصل اطمینان تصادفی برای 100 تحقق است.
اکثر مطالعات فقط بخشی از جمعیت را نمونه می کنند ، بنابراین نتایج کاملاً نمایانگر کل جمعیت نیست. هر تخمین به دست آمده از نمونه فقط به ارزش جمعیت نزدیک است. فواصل اعتماد به نفس به آمارشناسان اجازه می دهد تا بیان کنند که چقدر تخمین نمونه با ارزش واقعی در کل جامعه مطابقت دارد. اغلب آنها به صورت فاصله اطمینان 95٪ بیان می شوند. به طور رسمی ، یک فاصله اطمینان 95٪ برای یک مقدار دامنه ای است که در صورت تکرار نمونه برداری و تجزیه و تحلیل در همان شرایط (ارائه مجموعه داده های مختلف) ، بازه شامل 95٪ از کل موارد ممکن است مقدار واقعی (جمعیت) را شامل شود. . این نه مفهوم را میرسانند که احتمال این که ارزش واقعی در فاصله اطمینان 95٪ است. از مکررچشم انداز ، چنین ادعایی حتی معقول نیست ، زیرا مقدار واقعی یک متغیر تصادفی نیست . یا مقدار واقعی درون بازه معین است یا نیست. با این حال ، درست است که قبل از نمونه گیری از هر داده و نقشه ای برای چگونگی ساخت فاصله اطمینان حاصل شود ، احتمال 95٪ است که بازه هنوز محاسبه شده مقدار واقعی را پوشش دهد: در این مرحله ، محدوده بازه متغیرهای تصادفی هنوز قابل مشاهده است . یکی از رویکردهایی که بازه ای را به همراه دارد که می توان آن را تعبیر کرد که احتمالاً مقدار واقعی را در خود جای داده است ، استفاده از یک فاصله معتبر از آمار بیزی است : این رویکرد به روش دیگری برای تفسیر آنچه از «احتمال» منظور شده است بستگی دارد.، این به عنوان یک احتمال بیزی است .
در اصل فواصل اطمینان می تواند متقارن یا نامتقارن باشد. یک فاصله زمانی می تواند نامتقارن باشد زیرا برای یک پارامتر به عنوان مرز پایین یا بالا کار می کند (فاصله سمت چپ یا فاصله یک طرف سمت راست) ، اما همچنین می تواند نامتقارن باشد زیرا فاصله دو طرفه ساخته شده است و تقارن را نقض می کند. بعضی اوقات محدوده های یک فاصله اطمینان به صورت غیرمتعارف رسیده می شوند و از اینها برای تقریب مرزهای واقعی استفاده می شود.
اهمیت [ ویرایش ]
مقاله اصلی: اهمیت آماری
آمار به ندرت جواب سؤالی را که در زیر تجزیه و تحلیل قرار می گیرد ، پاسخ ساده ای دارد. تفسیر اغلب به سطح اهمیت آماری که برای اعداد اعمال می شود پایین می آید و اغلب به احتمال وجود یک مقدار با دقت رد فرضیه پوچ (که بعضاً به آن مقدار p گفته می شود ) اشاره دارد.
در این نمودار خط مشکی توزیع احتمال برای آماری آزمون است ، منطقه بحرانی مجموعه ای از مقادیر در سمت راست نقطه داده مشاهده شده (مقدار مشاهده شده آماری آزمون) است و مقدار p با سطح سبز نشان داده شده است.
رویکرد استاندارد [50] آزمایش یک فرضیه تهی علیه یک فرضیه جایگزین است. منطقه بحرانی مجموعه ای از ارزش برآوردگر است که منجر به رد فرضیه صفر است. احتمال خطای نوع I از این رو احتمال اینکه تخمینگر متعلق به منطقه بحرانی باشد با توجه به اینکه فرضیه تهی صحیح است ( اهمیت آماری ) است و احتمال خطای نوع II این احتمال است که تخمینگر متعلق به منطقه بحرانی داده نشده باشد. که فرضیه جایگزین درست است. قدرت آماری از آزمون احتمال این که آن را به درستی فرضیه صفر را رد فرضیه صفر که نادرست است.
مراجعه به اهمیت آماری لزوماً به معنای این نیست که نتیجه کلی از نظر دنیای واقعی قابل توجه است. به عنوان مثال ، در یک مطالعه بزرگ از یک دارو ممکن است نشان داده شود که این دارو از نظر آماری دارای یک اثر مفید از نظر آماری اما بسیار ناچیز است ، به گونه ای که بعید است این دارو به طور چشمگیری به بیمار کمک کند.
اگرچه در اصل ممکن است سطح قابل قبول از اهمیت آماری در معرض بحث باشد ، مقدار p کمترین سطح اهمیت است که به آزمون اجازه می دهد فرضیه تهی را رد کند. این آزمون از نظر منطقی معادل این است که بگوییم p-value یک احتمال است ، با فرض اینکه فرضیه تهی صحیح باشد ، مشاهده یک نتیجه حداقل به همان اندازه آماری آزمون است . بنابراین هرچه مقدار p کمتر باشد احتمال ارتکاب خطای نوع I نیز کمتر است.
بعضی از مشکلات معمولاً با این چهارچوب همراه هستند (به نقد تست فرضیه مراجعه کنید ):
- تفاوتی که از نظر آماری بسیار قابل توجه است ، هنوز هم می تواند هیچ اهمیت عملی نداشته باشد ، اما می توان تست های درستی را تدوین کرد تا این امر را پاسخگو باشد. یک پاسخ شامل فراتر از گزارش کردن فقط سطح اهمیت است تا در هنگام گزارش اینکه فرضیه رد شده یا پذیرفته شده است ، مقدار p- Value را شامل شود . مقدار p اما ، اندازه یا اهمیت اثر مشاهده شده را نشان نمی دهد و همچنین می تواند اهمیت اختلافات جزئی را در مطالعات بزرگ اغراق کند. یک روش بهتر و متداول تر گزارش دادن فواصل اطمینان است . اگرچه اینها از همان محاسبات آزمایشات فرضیه یا p تولید می شونداز نظر ارزش ، آنها هر دو اندازه اثر و عدم اطمینان پیرامون آن را توصیف می کنند.
- مغالطه شرط تحویل داده شده ، باطل بودن دادستان : انتقاداتی ایجاد می شود زیرا رویکرد آزمایش فرضیه ، یک فرضیه (فرضیه تهی ) را مجبور می کند که مورد علاقه قرار گیرد ، زیرا آنچه که ارزیابی می شود ، احتمال نتیجه مشاهده شده با توجه به فرضیه تهی بودن و نه احتمال آن است. فرضیه تهی با توجه به نتیجه مشاهده شده. جایگزینی برای این روش توسط استنباط بیزی ارائه می شود ، اگرچه نیاز به ایجاد احتمال قبلی دارد . [54]
- رد فرضیه تهی به طور خودکار فرضیه جایگزین را اثبات نمی کند.
- از آنجایی که همه چیز در آمار استنباطی به اندازه نمونه متکی است و بنابراین ممکن است مقادیر p-مقادیر زیر دم چربی محاسبه شود. [ نیاز به توضیح ]
مثالها [ ویرایش ]
برخی از آزمونها و روشهای آماری شناخته شده عبارتند از:
- تحلیل واریانس (ANOVA)
- آزمون مجذور کای
- همبستگی
- تحلیل عاملی
- مان ویتنی U
- میانگین انحراف وزن مربع (MSWD)
- ضریب همبستگی پیرسون محصول-لحظه
- تجزیه و تحلیل رگرسیون
- ضریب همبستگی رتبه Spearman
- آزمون t دانش آموزان
- تحلیل سری زمانی
- تجزیه و تحلیل مشترک
تجزیه و تحلیل داده های اکتشافی [ ویرایش ]
مقاله اصلی: تجزیه و تحلیل داده های اکتشافی
تجزیه و تحلیل داده های اکتشافی ( EDA ) یک رویکرد برای تجزیه و تحلیل مجموعه داده ها برای خلاصه کردن ویژگی های اصلی آنها ، اغلب با روش های بصری است. یک مدل آماری می تواند مورد استفاده قرار گیرد یا نباشد ، اما در درجه اول EDA برای دیدن آنچه داده ها می تواند فراتر از مدل سازی رسمی یا کار تست فرضیه به ما بگوید.
سوء استفاده [ ویرایش ]
مقاله اصلی: سوءاستفاده از آمار
سوءاستفاده از آمار می تواند خطاهای ظریف اما جدی در توصیف و تفسیر ایجاد کند - ظریف به این معنا که حتی متخصصان باتجربه مرتکب چنین خطاهایی می شوند و جدی به این معنا که می توانند منجر به خطاهای ویرانگر تصمیم شوند. به عنوان مثال ، سیاست های اجتماعی ، تمرین پزشکی و قابلیت اطمینان ساختارهایی مانند پل ها همه به استفاده صحیح از آمار متکی هستند.
حتی وقتی تکنیک های آماری به درستی به کار گرفته شوند ، تفسیر نتایج برای کسانی که فاقد تخصص هستند دشوار است. اهمیت آماری از یک روند در داده که تا چه حد که یک روند را می توان با تغییرات تصادفی در ایجاد اندازه گیری نمونه ممکن است با یک حس بصری از اهمیت آن را قبول ندارند. به مجموعه مهارتهای آماری اساسی (و شک و تردید) که افراد باید در زندگی روزمره خود به درستی با آنها برخورد کنند ، به سواد آماری گفته می شود .
این تصور عمومی وجود دارد که دانش آماری را با پیدا کردن راه هایی برای تفسیر فقط داده هایی که برای مجری مطلوب است ، عمداً سوءاستفاده می کنند. [55] یک عدم اعتماد و سوء تفاهم از آمار با نقل قول همراه است ، " سه نوع دروغ وجود دارد: دروغ ، دروغ لعنتی و آمار ". سوءاستفاده از آمار می تواند هم ناخواسته و هم عمدی باشد ، و کتاب How to Lie with Statistics [55] طیف وسیعی از ملاحظات را تشریح می کند. در تلاش برای روشن شدن استفاده و سوءاستفاده از آمار ، بررسی تکنیک های آماری مورد استفاده در زمینه های خاص (به عنوان مثال Warne، Lazo، Ramos، and Ritter (2012)) انجام شده است. [56]
راه های جلوگیری از سوءاستفاده از آمار شامل استفاده از نمودارهای مناسب و جلوگیری از تعصب است . [57] سوءاستفاده می تواند هنگامی اتفاق بیفتد که نتیجه گیری ها بیش از حد تخریب شده و ادعا می شود نماینده بیش از آنچه واقعاً هستند ، باشد ، غالباً با عمد یا ناخودآگاه مشرف به تعصب نمونه برداری. [58] نمودارهای نوار مسلما ساده ترین نمودارها برای استفاده و درک هستند و می توان آنها را با دستی یا با برنامه های رایانه ای ساده ساخت. [57] متأسفانه ، اکثر مردم به دنبال تعصب یا خطا نیستند ، بنابراین متوجه نمی شوند. بنابراین ، مردم اغلب ممکن است باور داشته باشند که چیزی صادق است ، حتی اگر به خوبی نمایش داده نشود . [58]برای اینکه داده های جمع آوری شده از آمار قابل باور و دقیق باشد ، نمونه گرفته شده باید نماینده کل باشد. [59] به گفته هاف ، "قابلیت اطمینان یک نمونه توسط [تعصب] از بین می رود ... به خود اجازه دهید تا شک و تردید به وجود بیاید." [60]
برای کمک به درک آمار ، هاف یک سری سؤال را در هر مورد مطرح کرد: [61]
- چه کسی چنین می گوید؟ (آیا او یک تبر برای خرد کردن دارد؟)
- چگونه او می داند؟ (آیا او منابع لازم برای شناخت واقعیت ها را دارد؟)
- چه چیزی گم شده است؟ (آیا او یک تصویر کامل به ما می دهد؟)
- آیا کسی موضوع را تغییر داده است؟ (آیا او پاسخ صحیح برای مسئله اشتباه به ما پیشنهاد می دهد؟)
- معنی داره؟ (آیا نتیجه گیری وی منطقی و مطابق با آنچه قبلاً می دانیم سازگار است؟)
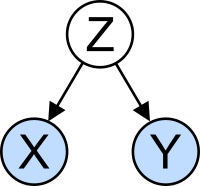
مخدوش کننده متغیر مشکل: X و Y ممکن است ارتباط، نه به خاطر رابطه علی بین آنها وجود دارد، اما به دلیل هر دو در یک متغیر سوم بستگی دارد Z . Z یک عامل گیج کننده نامیده می شود.
تفسیر نادرست: همبستگی [ ویرایش ]
مفهوم همبستگی به ویژه برای سردرگمی احتمالی ناشی از آن قابل توجه است. تجزیه و تحلیل آماری از یک مجموعه داده اغلب نشان می دهد که دو متغیر (خصوصیات) از جمعیت مورد نظر با هم متفاوت هستند ، انگار به هم متصل هستند. به عنوان مثال ، مطالعه درآمدهای سالانه که همچنین به بررسی سن مرگ می پردازد ، ممکن است نشان دهد که افراد فقیر نسبت به افراد مرفه زندگی کمتری دارند. گفته می شود که این دو متغیر با یکدیگر ارتباط دارند. با این حال ، آنها ممکن است یا ممکن است دلیل یکدیگر نباشند. این پدیده همبستگی می تواند توسط یک پدیده سوم ، که قبلاً مورد بررسی قرار نگرفته باشد ، ایجاد شود به نام متغیر کمین یا متغیر مخدوش کننده. به همین دلیل ، هیچ راهی برای استنباط فوری وجود رابطه علی بین دو متغیر وجود ندارد. (ببینید همبستگی به معنای علیت نیست .)
برنامه ها [ ویرایش ]
آمار کاربردی ، آمار نظری و آمار ریاضی [ ویرایش ]
آمار توصیفی شامل آمار توصیفی و کاربرد آمار استنباطی است. [62] [63] آمار نظری مربوط به استدلالهای منطقی استدلال شده در توجیه رویکردهای استنتاج آماری و همچنین شامل آمارهای ریاضی است . آمار ریاضی نه تنها دستکاری توزیع احتمال لازم برای به دست آوردن نتایج مربوط به روش های تخمین و استنتاج ، بلکه جنبه های مختلفی از آمار محاسباتی و طراحی آزمایشات را نیز شامل می شود .
یادگیری ماشین و داده کاوی [ ویرایش ]
مدل های یادگیری ماشینی مدل های آماری و احتمالی هستند که از طریق استفاده از الگوریتم های محاسباتی الگوهای موجود در داده ها را ضبط می کنند.
آمار در جامعه [ ویرایش ]
آمار در طیف گسترده ای از رشته های دانشگاهی اعم از علوم طبیعی و اجتماعی ، دولتی و تجاری قابل استفاده است. مشاوران آماری می توانند به سازمانها و شرکتهایی که تخصص داخلی ندارند مربوط به سؤالات خاص خود باشند.
محاسبه آماری [ ویرایش ]
گرتل ، نمونه ای از بسته های آماری منبع باز
مقاله اصلی: آمار محاسباتی
افزایش سریع و پایدار قدرت محاسباتی که از نیمه دوم قرن بیستم شروع می شود ، تأثیر قابل توجهی در عملکرد علم آماری داشته است. مدلهای آماری اولیه تقریباً همیشه از کلاس مدل های خطی بودند ، اما رایانه های قدرتمند همراه با الگوریتم های عددی مناسب باعث افزایش علاقه به مدل های غیرخطی (مانند شبکه های عصبی ) و همچنین ایجاد انواع جدید مانند مدل های خطی تعمیم یافته شدند. و مدل های چند سطحی .
افزایش قدرت محاسباتی نیز به محبوبیت رو به رشد روش محاسباتی فشرده بر اساس منجر بازنمونه گیری ، از جمله آزمایش های قلب و تحریف و راه انداز ، در حالی که روش های مانند نمونهگیری گیبس استفاده ساخته شده از مدل های بیزی بیشتر امکان پذیر است. انقلاب رایانه ای با تأکید جدید بر آمارهای "تجربی" و "تجربی" برای آینده آماری مؤثر است. تعداد زیادی از نرم افزارهای آماری عمومی و ویژه برای هم اکنون در دسترس هستند. نمونه هایی از نرم افزارهای موجود که توانایی محاسبات آماری پیچیده را دارند شامل برنامه هایی مانند Mathematica ، SAS ، SPSS و R می باشد.
آمار مربوط به ریاضیات یا هنرها [ ویرایش ]
به طور سنتی ، آمار مربوط به ترسیم استنتاج ها با استفاده از یک روش نیمه استاندارد بود که در اکثر علوم "یادگیری لازم" بود. [ نیاز به استناد ] این سنت با استفاده از آمار در زمینه های غیر استنباطی تغییر کرده است. آنچه در گذشته موضوعی خشک تلقی می شد ، که در بسیاری از زمینه ها به عنوان یک مدرک تحصیلی مورد توجه قرار گرفته بود ، اکنون با شور و شوق مشاهده می شود. [ طبق چه کسی؟ ] در ابتدا توسط برخی از طرفداران ریاضی به سخره گرفت، در حال حاضر روش ضروری در مناطق خاص در نظر گرفته.
- در تئوری اعداد ، توطئه های پراكنده داده های ایجاد شده توسط یك تابع توزیع ممكن است با ابزارهای آشنا مورد استفاده در آمار برای آشكارسازی الگوهای زمینه ای تبدیل شوند ، كه می تواند منجر به فرضیه ها شود.
- روش های آماری از جمله روش های پیش بینی کننده در پیش بینی با نظریه آشوب و هندسه فراکتالی ترکیب شده اند تا آثار ویدیویی را ایجاد کنند که از نظر زیبایی بسیار خوبی دارند. [ نیاز به استناد ]
- هنر فرایند از جکسون پولاک در آزمایش های هنری تکیه به موجب آن توزیع اساسی در طبیعت هنری نشان داد. [ نیاز به استناد ] با ظهور رایانه ها ، از روشهای آماری برای رسمی سازی چنین فرآیندهای طبیعی مبتنی بر توزیع برای ساخت و تحلیل هنر ویدیویی متحرک استفاده شد. [ نیاز به استناد ]
- روش های آماری ممکن است به صورت پیش فرض در هنر عملکرد استفاده شود ، همانطور که در یک ترفند کارت بر اساس یک فرآیند مارکوف که فقط برخی از زمان ها را کار می کند ، به مناسبت آن می توان با استفاده از روش آماری پیش بینی کرد.
- از آمار می توان برای ایجاد پیش بینی های هنری استفاده کرد ، همانطور که در موسیقی آماری یا تصادفی ابداع شده توسط Iannis Xenakis ، جایی که موسیقی خاص عملکرد است. اگرچه این نوع هنری همیشه مطابق آنچه انتظار می رود ظاهر نمی شود ، اما به گونه ای رفتار می کند که با استفاده از آمار قابل پیش بینی و تنظیم باشد.
رشته های تخصصی [ ویرایش ]
مقاله اصلی: لیست زمینه های کاربرد آمار
: روش های آماری در طیف گسترده ای از انواع پژوهش های علمی و اجتماعی، از جمله استفاده آمار زیستی ، زیست شناسی محاسباتی ، جامعه شناسی محاسباتی ، زیست شناسی شبکه ، علوم اجتماعی ، جامعه شناسی و تحقیقات اجتماعی . برخی از زمینه های تحقیق از آمارهای کاربردی چنان گسترده استفاده می کنند که اصطلاحات تخصصی دارند . این رشته ها عبارتند از:
- علم آماری (ارزیابی ریسک در صنایع بیمه و دارایی)
- اقتصاد اطلاعاتی کاربردی
- ستاره شناسی (ارزیابی آماری داده های نجومی)
- آمار زیستی
- آمار تجارت
- شیمی سنجی (برای تجزیه و تحلیل داده های شیمی )
- داده کاوی (استفاده از آمار و شناخت الگوی برای کشف دانش از داده ها)
- علم داده
- جمعیت شناسی (مطالعه آماری جمعیت)
- اقتصاد سنجی (تجزیه و تحلیل آماری داده های اقتصادی)
- آمار انرژی
- آمار مهندسی
- اپیدمیولوژی (تجزیه و تحلیل آماری بیماری)
- جغرافیا و سیستم های اطلاعات جغرافیایی ، به طور خاص در تجزیه و تحلیل مکانی
- پردازش تصویر
- مربیان ( قانون )
- آمار پزشکی
- علوم سیاسی
- آمار روانشناختی
- مهندسی قابلیت اطمینان
- آمار اجتماعی
- مکانیک آماری
علاوه بر این ، انواع خاصی از تجزیه و تحلیل آماری وجود دارد که اصطلاحات و روش تخصصی خود را نیز توسعه داده اند:
- راه اندازی مجدد بوت استرپ / جک زن
- آمار چند متغیره
- طبقه بندی آماری
- تجزیه و تحلیل داده های ساختاری (آمار)
- مدل سازی معادلات ساختاری
- روش تحقیق
- تجزیه و تحلیل بقا
- آمار در ورزش های مختلف ، به ویژه بیس بال - که به عنوان سابمتریک شناخته می شود - وکریکت
آمار نیز یک ابزار اساسی در تجارت و تولید است. برای درک تغییرپذیری سیستم های اندازه گیری ، فرآیندهای کنترل (مانند کنترل فرآیند آماری یا SPC) ، برای جمع بندی داده ها و تصمیم گیری مبتنی بر داده استفاده می شود. در این نقش ها ، یک ابزار کلیدی و شاید تنها ابزار قابل اعتماد است.
همچنین مشاهده کنید [ ویرایش ]
| منابع كتابخانه درباره آمار |
مقاله اصلی: خلاصه آمار
- تخمین فراوان
- علم داده
- واژه نامه احتمالی و آمار
- لیست انجمنهای آماری دانشگاهی
- لیست نشریات مهم در آمار
- لیست خدمات آماری ملی و بین المللی
- لیست بسته های آماری (نرم افزاری)
- لیست مقالات آماری
- لیست مراکز مشاوره آماری دانشگاه
- نماد احتمالی و آمار
مبانی و زمینه های اصلی آمار

 در این وبلاگ به ریاضیات و کاربردهای آن و تحقیقات در آنها پرداخته می شود. مطالب در این وبلاگ ترجمه سطحی و اولیه است و کامل نیست.در صورتی سوال یا نظری در زمینه ریاضیات دارید مطرح نمایید .در صورت امکان به آن می پردازم. من دوست دارم برای یافتن پاسخ به سوالات و حل پروژه های علمی با دیگران همکاری نمایم.در صورتی که شما هم بامن هم عقیده هستید با من تماس بگیرید.
در این وبلاگ به ریاضیات و کاربردهای آن و تحقیقات در آنها پرداخته می شود. مطالب در این وبلاگ ترجمه سطحی و اولیه است و کامل نیست.در صورتی سوال یا نظری در زمینه ریاضیات دارید مطرح نمایید .در صورت امکان به آن می پردازم. من دوست دارم برای یافتن پاسخ به سوالات و حل پروژه های علمی با دیگران همکاری نمایم.در صورتی که شما هم بامن هم عقیده هستید با من تماس بگیرید.