5-چهار وجهی

توسط علی رضا نقش نیلچی | پنجشنبه پنجم بهمن ۱۴۰۲ | 18:7

خصوصیات عمومی [ ویرایش ]

حجم [ ویرایش ]

حجم یک چهار وجهی با فرمول حجم هرم به دست می آید:

$V={\frac {1}{3}}A_{0}\,h\,$

که در آن A 0 مساحت قاعده و h ارتفاع قاعده تا راس است. این برای هر یک از چهار انتخاب پایه صدق می کند، بنابراین فواصل راس ها تا وجوه مقابل با مناطق این وجه ها نسبت معکوس دارد.

برای چهار وجهی با رئوس a = ( a 1 , a 2 , a 3 ) , b = ( b 1 , b 2 , b 3 ) , c = ( c 1 , c 2 , c 3 ) و d = ( d 1 , d 2 , d 3 ) , حجم است

1/| det ( a − d , b − d , c − d )|

، یا هر ترکیب دیگری از جفت رئوس که یک نمودار ساده متصل را تشکیل می دهند . این را می توان با استفاده از یک محصول نقطه ای و یک محصول متقاطع بازنویسی کرد و نتیجه داد

. $V={\frac {|(\mathbf {a} -\mathbf {d} )\cdot ((\mathbf {b} -\mathbf {d} )\times (\mathbf {c} -\mathbf {d} ))|}{6}}.$

اگر مبدأ سیستم مختصات منطبق بر راس d انتخاب شود ، d = 0 ، بنابراین

$V={\frac {|\mathbf {a} \cdot (\mathbf {b} \times \mathbf {c} )|}{6}}،$

که در آن a ، b و c نشان دهنده سه یال هستند که در یک راس به هم می رسند، و a · ( b × c ) یک حاصل ضرب سه گانه اسکالر است . با مقایسه این فرمول با فرمول مورد استفاده برای محاسبه حجم موازی ، نتیجه می گیریم که حجم یک چهار وجهی برابر است با1/6از حجم هر متوازی الاضلاع که سه یال همگرا با آن مشترک است.

قدر مطلق حاصلضرب سه گانه اسکالر را می توان به صورت مقادیر مطلق دترمینان های زیر نشان داد:

$6\cdot V={\begin{Vmatrix}\mathbf {a} &\mathbf {b} &\mathbf {c} \end{Vmatrix}}$ یا $6\cdot V={\begin{Vmatrix}\mathbf {a} \\\mathbf {b} \\\mathbf {c} \end{Vmatrix}}$ جایی که ، ${\begin{cases}\mathbf {a} =(a_{1},a_{2},a_{3}),\\\mathbf {b} =(b_{1},b_{2} ,b_{3})،\\\mathbf {c} =(c_{1},c_{2},c_{3})،\end{موارد}}$ به صورت بردارهای سطر یا ستون بیان می شوند.

از این رو

⋅ $36\cdot V^{2}={\begin{vmatrix}\mathbf {a^{2}} &\mathbf {a} \cdot \mathbf {b} &\mathbf {a} \cdot \mathbf {c} \\\mathbf {a} \cdot \mathbf {b} &\mathbf {b^{2}} &\mathbf {b} \cdot \mathbf {c} \\\mathbf {a} \cdot \ mathbf {c} &\mathbf {b} \cdot \mathbf {c} &\mathbf {c^{2}} \end{vmatrix}}$

جایی که

⁡. ${\begin{cases}\mathbf {a} \cdot \mathbf {b} =ab\cos {\gamma },\\\mathbf {b} \cdot \mathbf {c} =bc\cos {\ alpha },\\\mathbf {a} \cdot \mathbf {c} =ac\cos {\beta }.\end{موارد}}$

که می دهد

$V={\frac {abc}{6}}{\sqrt {1+2\cos {\alpha }\cos {\beta }\cos {\gamma }-\cos ^{2}{\alpha }-\cos ^{2}{\beta }-\cos ^{2}{\gamma }}},\,$

که α , β , γ زوایای صفحه ای هستند که در راس d قرار دارند . زاویه α ، زاویه بین دو یال است که راس d را به رئوس b و c متصل می کند . زاویه β ، این کار را برای رئوس a و c انجام می دهد ، در حالی که γ ، با موقعیت رئوس a و b تعریف می شود. تعریف می شود .

اگر نیازی به d = 0 نداشته باشیم

$6\cdot V=\left|\det \left({\begin{matrix}a_{1}&b_{1}&c_{1}&d_{1}\\a_{2}&b_{2}&c_{ 2}&d_{2}\\a_{3}&b_{3}&c_{3}&d_{3}\\1&1&1&1\end{ماتریس}}\راست)\راست|\,.$

با توجه به فواصل بین رئوس یک چهار وجهی، حجم را می توان با استفاده از دترمینان کیلی-منجر محاسبه کرد :

$288\cdot V^{2}={\begin{vmatrix}0&1&1&1&1\\1&0&d_{12}^{2}&d_{13}^{2}&d_{14}^{2}\\1&d_{12 }^{2}&0&d_{23}^{2}&d_{24}^{2}\\1&d_{13}^{2}&d_{23}^{2}&0&d_{34}^{2}\\1&d_ {14}^{2}&d_{24}^{2}&d_{34}^{2}&0\end{vmatrix}}$

که در آن زیرنویسهای i , j ∈ {1, 2, 3, 4} نشان دهنده رئوس { a , b , c , d } و d ij فاصله زوجی بین آنهاست - یعنی طول یال که دو راس را به هم متصل می کند. مقدار منفی دترمینان به این معنی است که یک چهار وجهی را نمی توان با فاصله های داده شده ساخت. این فرمول، که گاهی فرمول تارتالیا نامیده می‌شود ، اساساً ناشی از نقاش پیرو دلا فرانچسکا در قرن پانزدهم است، به‌عنوان یک آنالوگ سه بعدی از فرمول قرن اول هرون برای مساحت مثلث. [16]

فرض کنید a، b، c سه یال باشند که در یک نقطه به هم می رسند و x، y، z یال های مقابل باشند. فرض کنید V حجم چهار وجهی باشد. سپس [17]

$V={\frac {\sqrt {4a^{2}b^{2}c^{2}-a^{2}X^{2}-b^{2}Y^{2}- c^{2}Z^{2}+XYZ}}{12}}$

جایی که

${\begin{aligned}X&=b^{2}+c^{2}-x^{2},\\Y&=a^{2}+c^{2}-y^{2} ,\\Z&=a^{2}+b^{2}-z^{2}.\end{تراز شده}}$

فرمول فوق از شش طول یال استفاده می کند و فرمول زیر از سه طول یال و سه زاویه استفاده می کند.

$V={\frac {abc}{6}}{\sqrt {1+2\cos {\alpha }\cos {\beta }\cos {\gamma }-\cos ^{2}{\alpha }-\cos ^{2}{\beta }-\cos ^{2}{\gamma }}}$

فرمول نوع حواصیل برای حجم یک چهار وجهی [ ویرایش ]

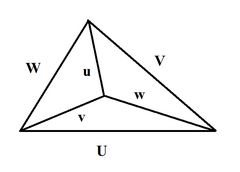
شش طول یال چهار وجهی

اگر U , V , W , u , v , w طول یال های چهار ضلعی باشند (سه ضلعی اول یک مثلث را تشکیل می دهند، با u در مقابل U ، v مقابل V ، w در مقابل W )، پس [18]

$V={\frac {\sqrt {\,(-p+q+r+s)\,(p-q+r+s)\,(p+q-r+s)\,(p +q+rs)}}{192\,u\,v\,w}}$

جایی که

${\begin{aligned}p&={\sqrt {xYZ}},&q&={\sqrt {yZX}},&r&={\sqrt {zXY}},&s&={\sqrt {xyz}},\ پایان{تراز شده}}$

${\begin{تراز شده}X&=(w-U+v)\,(U+v+w),&x&=(U-v+w)\,(v-w+U),\\Y& =(u-V+w)\,(V+w+u),&y&=(V-w+u)\,(w-u+V),\\Z&=(v-W+u)\, (W+u+v)،&z&=(W-u+v)\,(u-v+W).\end{تراز شده}}$

تقسیم کننده صدا [ ویرایش ]

هر صفحه ای که حاوی دو وسط (اتصال نقاط میانی یال های مخالف) یک چهار وجهی باشد ، حجم چهار وجهی را به دو نیم می کند . [19]

جلد غیر اقلیدسی [ ویرایش ]

برای چهار وجهی در فضای هذلولی یا در هندسه بیضوی سه بعدی ، زوایای دو وجهی چهار وجهی شکل و در نتیجه حجم آن را تعیین می کند. در این موارد، حجم با فرمول موراکامی-یانو داده می شود . [20] با این حال، در فضای اقلیدسی، مقیاس کردن یک چهار وجهی، حجم آن را تغییر می‌دهد، اما زوایای دو وجهی آن را تغییر نمی‌دهد، بنابراین چنین فرمولی نمی‌تواند وجود داشته باشد.

فاصله بین یال ها [ ویرایش ]

هر دو یال متضاد چهار وجهی روی دو خط اریب قرار دارند و فاصله بین یال ها به عنوان فاصله بین دو خط اریب تعریف می شود. فرض کنید d فاصله بین خطوط اریب تشکیل شده توسط یال های مخالف a و b - c باشد که در اینجا محاسبه می شود . سپس فرمول حجم دیگری با استفاده از

$V={\frac {d|(\mathbf {a} \times \mathbf {(bc)} )|}{6}}.$

خصوصیات مشابه با خواص مثلث [ ویرایش ]

چهار ضلعی دارای خواص زیادی شبیه به مثلث است که از جمله آنها می توان به درون کره، محیط، چهار وجهی میانی و بیرون کره اشاره کرد. دارای مراکز مربوطه مانند مرکز، مرکز، مرکز، مرکز اسپیکر و نقاطی مانند مرکز است. با این حال، به طور کلی هیچ مرکز مرکزی به معنای متقاطع ارتفاعات وجود ندارد. [21]

گاسپارد مونگ مرکزی را پیدا کرد که در هر چهار وجهی وجود دارد، که اکنون به عنوان نقطه مونگ شناخته می شود : نقطه ای که در آن شش صفحه میانی یک چهار وجهی تلاقی می کنند. سطح میانی به صفحه‌ای گفته می‌شود که متعامد به یال‌ای است که هر دو راس را به هم می‌پیوندد که شامل مرکز یک یال مقابل است که از اتصال دو راس دیگر تشکیل شده است. اگر ارتفاعات چهار وجهی همدیگر را قطع کنند، آنگاه نقطه مونگ و مرکز عمود بر هم منطبق می شوند و کلاس چهار وجهی متعامد را به دست می دهند .

یک خط متعامد از نقطه مونگ به هر وجهی که در نقطه وسط پاره خط بین مرکز قائم وجه و پای ارتفاعی که از راس مخالف کاهش یافته است، با آن صورت برخورد کند.

پاره خطی که یک راس چهار وجهی را به مرکز وجه مقابل می‌پیوندد، میانه و پاره خطی را که نقاط میانی دو یال مخالف را به هم می‌پیوندد، دو میانی چهار وجهی می‌گویند. از این رو در چهار وجهی چهار میانه و سه دوسطح وجود دارد. این هفت پاره خط همگی در نقطه ای به نام مرکز چهار وجهی همزمان هستند. [22] علاوه بر این، چهار میانه در نسبت 3:1 توسط مرکز تقسیم می شوند (به قضیه کوماندینو مراجعه کنید ). مرکز یک چهار وجهی نقطه وسط بین نقطه مونگ و مرکز محیط آن است. این نقاط خط اویلر چهار وجهی را که مشابه خط اویلر است مشخص می کند یک مثلث است مشخص می کند.

دایره نه نقطه ای مثلث کلی دارای یک آنالوگ در محیط چهار وجهی میانی چهار وجهی است. این کره دوازده نقطه ای است و علاوه بر مرکز چهار وجه چهار وجهی مرجع، از چهار نقطه جایگزین اویلر ، یک سوم مسیر از نقطه مونگ به سمت هر یک از چهار راس عبور می کند. در نهایت از چهار نقطه پایه خطوط متعامد رها شده از هر نقطه اویلر به سمت وجهی می گذرد که شامل رأسی نیست که نقطه اویلر را ایجاد کرده است. [23]

مرکز T کره دوازده نقطه ای نیز روی خط اویلر قرار دارد. این مرکز بر خلاف همتای مثلثی خود، یک سوم راه را از نقطه مونژ M به سمت مرکز دور قرار می دهد. همچنین، یک خط متعامد از طریق T به یک وجه انتخابی با دو خط متعامد دیگر به همان وجه همسطح است. اولی یک خط متعامد است که از نقطه اویلر مربوطه به وجه انتخاب شده می گذرد. خط دوم یک خط متعامد است که از مرکز وجه انتخاب شده می گذرد. این خط متعامد از مرکز دوازده نقطه ای در میانه راه بین خط متعامد نقطه اویلر و خط متعامد مرکز قرار دارد. علاوه بر این، برای هر صورت، مرکز دوازده نقطه ای در نقطه میانی نقطه اویلر مربوطه و مرکز قائم برای آن صورت قرار دارد.

شعاع کره دوازده نقطه ای یک سوم شعاع محیطی چهار وجهی مرجع است.

یک رابطه بین زوایای ساخته شده توسط وجوه یک چهار وجهی کلی وجود دارد که توسط [24] ارائه شده است.

${\begin{vmatrix}-1&\cos {(\alpha _{12})}&\cos {(\alpha _{13})}&\cos {(\alpha _{14})}\ \\cos {(\alpha _{12})}&-1&\cos {(\alpha _{23})}&\cos {(\alpha _{24})}\\\cos {(\alpha _ {13})}&\cos {(\alpha _{23})}&-1&\cos {(\alpha _{34})}\\\cos {(\alpha _{14})}&\cos {(\alpha _{24})}&\cos {(\alpha _{34})}&-1\\\end{vmatrix}}=0\,$

که α ij زاویه بین وجه i و j است .

میانه هندسی مختصات موقعیت راس یک چهار وجهی و مرکز ایزوگونیک آن، تحت شرایطی مشابه با موارد مشاهده شده برای یک مثلث، مرتبط است. لورنز لیندلوف دریافت که متناظر با هر چهار ضلعی معین، نقطه ای است که اکنون به عنوان مرکز ایزوگونیک شناخته می شود، O ، که در آن زوایای جامد فرورفته توسط وجوه برابر هستند، دارای مقدار مشترک π sr هستند، و در آن زوایای متضاد فرو می روند. یال ها برابر هستند [25] یک زاویه جامد π sr یک چهارم زاویه ای است که توسط کل فضا تحت تأثیر قرار می گیرد. هنگامی که تمام زوایای جامد در رئوس یک چهار وجهی کوچکتر از π sr باشد، O در داخل چهار وجهی قرار دارد و چون مجموع فواصل O تا رئوس حداقل است، O با میانه هندسی M رئوس منطبق است. . در صورتی که زاویه جامد در یکی از رئوس، v ، دقیقا π sr را اندازه گیری کند، سپس O و M با v منطبق شوند . با این حال، اگر یک چهار وجهی دارای راس v با زاویه جامد بزرگتر از π sr باشد، M همچنان با v مطابقت دارد ، اما O در خارج از چهار وجهی قرار دارد.

روابط هندسی [ ویرایش ]

چهار وجهی یک 3 سیمپلکس است . بر خلاف موارد دیگر جامدات افلاطونی، تمام رئوس یک چهار وجهی منظم از یکدیگر فاصله دارند (آنها تنها آرایش ممکن از چهار نقطه مساوی در فضای سه بعدی هستند).

چهار وجهی یک هرم مثلثی است و چهار وجهی منظم خود دوگانه است .

یک چهار ضلعی منظم را می توان به دو صورت در داخل یک مکعب جاسازی کرد به طوری که هر رأس یک راس مکعب و هر یال مورب یکی از وجوه مکعب باشد. برای یکی از این جاسازی ها، مختصات دکارتی رئوس هستند

(+1، +1، +1)؛

(-1، -1، +1)؛

(-1، +1، -1)؛

(+1، -1، -1).

این یک چهار ضلعی با طول یال 2 √ 2 به دست می دهد که در مرکز مبدا قرار دارد. برای چهار وجهی دیگر (که دوتایی نسبت به اولی است)، همه نشانه ها را معکوس کنید. این دو رأس چهار ضلعی که با هم ترکیب شده اند، رئوس یک مکعب هستند، که نشان می دهد چهار وجهی منتظم، 3- نیمه مکعب است .

استلا اکتانگولا .

حجم این چهار وجهی یک سوم حجم مکعب است. از ترکیب هر دو چهار وجهی، یک ترکیب چندوجهی منظم به دست می‌آید که ترکیب دو چهار وجهی یا استلا اکتان گولا نامیده می‌شود .

فضای داخلی استلا اکتانگولا یک هشت ضلعی است و به همین ترتیب، یک هشت ضلعی منتظم نتیجه بریدن چهار چهار ضلعی منتظم با نصف اندازه خطی (یعنی یکسو کردن) از یک چهار وجهی منظم است. چهار وجهی) از یک چهار ضلعی منظم است.

تعبیه فوق مکعب را به پنج چهار وجهی تقسیم می کند که یکی از آنها منظم است. در واقع، پنج، حداقل تعداد چهار وجهی مورد نیاز برای تشکیل یک مکعب است. برای مشاهده این موضوع، با شروع از یک چهار وجهی پایه با 4 راس، هر چهار وجهی اضافه شده حداکثر 1 راس جدید اضافه می کند، بنابراین حداقل 4 راس دیگر باید اضافه شود تا یک مکعب ساخته شود که دارای 8 راس است.

با درج چهار وجهی درون ترکیب منظم پنج مکعبی ، دو ترکیب منظم دیگر به دست می‌آید که شامل پنج و ده چهار وجهی است.

چهار وجهی منظم نمی تواند به تنهایی فضا را جدا کند ، اگرچه این نتیجه به اندازه کافی محتمل به نظر می رسد که ارسطو ادعا می کند امکان پذیر است. با این حال، دو چهار وجهی معمولی را می توان با یک هشت وجهی ترکیب کرد و یک لوزی ایجاد کرد که می تواند فضایی را به عنوان لانه زنبوری چهار وجهی - هشت وجهی ایجاد کند .

با این حال، چندین چهار وجهی نامنظم شناخته شده‌اند، که کپی‌هایی از آن‌ها می‌توانند فضا را کاشی کنند، به‌عنوان مثال طرح‌بندی مشخصه مکعب و دیسپنوئید لانه زنبوری چهار وجهی دیسپنوئید . لیست کامل همچنان یک مشکل باز است. [26]

اگر نیاز به یک شکل بودن چهار ضلعی را راحت کنید، می توانید فضا را تنها با استفاده از چهار وجهی به روش های مختلف کاشی کاری کنید. به عنوان مثال، می توان یک هشت وجهی را به چهار چهار وجهی یکسان تقسیم کرد و دوباره آنها را با دو چهار وجهی منظم ترکیب کرد. (به عنوان یک نکته جانبی: این دو نوع چهار وجهی حجم یکسانی دارند.)

چهار ضلعی در بین چندوجهی های یکنواخت منحصر به فرد است زیرا هیچ وجهی موازی ندارد.

قانون سینوس برای چهار وجهی و فضای همه اشکال چهار وجهی [ ویرایش ]

نوشتار اصلی: مثلثات چهار وجهی

نتیجه قانون معمول سینوس ها این است که در چهار وجهی با رئوس O , A , B , C داریم

$\sin \angle OAB\cdot \sin \angle OBC\cdot \sin \angle OCA=\sin \angle OAC\cdot \sin \angle OCB\cdot \sin \angle OBA.\,$

می توان دو طرف این هویت را مطابق با جهت گیری عقربه های ساعت و خلاف جهت عقربه های ساعت سطح مشاهده کرد.

با قرار دادن هر یک از چهار رأس در نقش O ، چهار هویت حاصل می شود، اما حداکثر سه تای آنها مستقل هستند: اگر اضلاع "جهت عقربه های ساعت" سه تای آنها ضرب شود و حاصل ضرب برابر حاصل ضرب شود. طرف های «ضدساعتگرد» همان سه هویت، و سپس عوامل مشترک از هر دو طرف لغو می شود، نتیجه هویت چهارم است.

سه زاویه زوایای یک مثلث هستند اگر و فقط در صورتی که مجموع آنها 180 درجه (رادیان π) باشد. چه شرطی در 12 زاویه لازم و کافی است که آنها 12 زاویه یک چهار وجهی باشند؟ واضح است که مجموع زوایای هر ضلع چهار وجهی باید 180 درجه باشد. از آنجایی که چهار مثلث از این قبیل وجود دارد، چهار محدودیت برای مجموع زاویه‌ها وجود دارد و تعداد درجه‌های آزادی از 12 به 8 کاهش می‌یابد. 8 را نه به 4 بلکه به 5 کاهش دهید، زیرا محدودیت چهارم مستقل از سه مورد اول نیست. بنابراین فضای تمام اشکال چهار وجهی 5 بعدی است. [27]

قانون کسینوس برای چهار وجهی [ ویرایش ]

نوشتار اصلی: مثلثات چهار وجهی

فرض کنید { P 1 , P 2 , P 3 , P 4 } نقاط یک چهار وجهی باشد. فرض کنید Δ i مساحت صورت مقابل راس P i باشد و θ ij زاویه دو وجهی بین دو وجه چهاروجهی مجاور یال P i P j باشد .

قانون کسینوس برای این چهار وجهی، [28] که مساحت وجوه چهاروجهی را به زوایای دو وجهی در مورد یک راس مرتبط می‌کند، با رابطه زیر به دست می‌آید:

$\Delta _{i}^{2}=\Delta _{j}^{2}+\Delta _{k}^{2}+\Delta _{l}^{2}-2(\ دلتا _{j}\Delta _{k}\cos \theta _{il}+\Delta _{j}\Delta _{l}\cos \theta _{ik}+\Delta _{k}\Delta _ {l}\cos \theta _{ij})$

نقطه داخلی [ ویرایش ]

فرض کنید P هر نقطه داخلی یک چهار وجهی با حجم V باشد که رئوس آن A , B , C و D باشد و نواحی وجه های مقابل آن F a , F b , F c و F d باشد . سپس [29] : ص62، #1609

$PA\cdot F_{\mathrm {a} }+PB\cdot F_{\mathrm {b} }+PC\cdot F_{\mathrm {c} }+PD\cdot F_{\mathrm {d} } \geq 9V.$

برای رئوس A ، B ، C و D ، نقطه داخلی P ، و پاهای J ، K ، L ، و M از عمودهای P به وجوه، و فرض کنید وجه ها مساحت مساوی دارند، سپس [29] : p.226 ، #215

$PA+PB+PC+PD\geq 3(PJ+PK+PL+PM).$

اینرادیوس [ ویرایش ]

با نشان دادن شعاع یک چهار وجهی به عنوان r و شعاع وجه های مثلثی آن به عنوان r i برای i = 1، 2، 3، 4، داریم [29] : p.81, #1990

${\frac {1}{r_{1}^{2}}}+{\frac {1}{r_{2}^{2}}}+{\frac {1}{r_{3} ^{2}}}+{\frac {1}{r_{4}^{2}}}\leq {\frac {2}{r^{2}}}،$

با برابری اگر و فقط اگر چهار وجهی منظم باشد.

اگر A 1 ، A 2 ، A 3 و A 4 مساحت هر وجه را نشان دهند، مقدار r با

$r={\frac {3V}{A_{1}+A_{2}+A_{3}+A_{4}}}$ .

این فرمول از تقسیم چهار وجهی به چهار چهار وجهی به دست می آید که نقاط آن سه نقطه یکی از وجوه اصلی و مرکز است. از آنجایی که چهار زیر چهار وجهی حجم را پر می کنند، داریم

$V={\frac {1}{3}}A_{1}r+{\frac {1}{3}}A_{2}r+{\frac {1}{3}}A_{3}r+ {\frac {1}{3}}A_{4}r$ .

شعاع محیطی[ ویرایش ]

شعاع محیطی یک چهار وجهی را با R مشخص کنید . فرض کنید a , b , c طول سه یال که در یک راس به هم می رسند و A , B , C طول یال های مقابل باشد. فرض کنید V حجم چهار وجهی باشد. سپس [30] [31]

آ $R={\frac {\sqrt {(aA+bB+cC)(aA+bB-cC)(aA-bB+cC)(-aA+bB+cC)}}{24V}}.$

مرکز دور [ ویرایش ]

مرکز دور یک چهار وجهی را می توان به صورت تقاطع سه صفحه نیمساز پیدا کرد. صفحه نیمساز به عنوان صفحه ای در مرکز و متعامد به یال چهار وجهی تعریف می شود. با این تعریف، مرکز C یک چهار وجهی با رئوس x 0 , x 1 , x 2 , x 3 می تواند به عنوان حاصلضرب ماتریس-بردار فرموله شود: [32]

${\begin{aligned}C&=A^{-1}B&{\text{where}}&\ &A=\left({\begin{matrix}\left[x_{1}-x_{0} \right]^{T}\\\left[x_{2}-x_{0}\right]^{T}\\\left[x_{3}-x_{0}\right]^{T}\ end{matrix}}\right)&\ &{\text{and}}&\ &B={\frac {1}{2}}\left({\begin{matrix}\|x_{1}\|^ {2}-\|x_{0}\|^{2}\\\|x_{2}\|^{2}-\|x_{0}\|^{2}\\\|x_{3 }\|^{2}-\|x_{0}\|^{2}\end{ماتریس}}\راست)\\\end{تراز شده}}$

بر خلاف مرکز، مرکز محیط ممکن است همیشه در داخل یک چهار وجهی قرار نگیرد. همانند یک مثلث منفرد، مرکز محیط خارج از جسم برای یک چهار وجهی منفرد است.

Centroid [ ویرایش ]

مرکز جرم چهار وجهی به عنوان میانگین حسابی چهار رأس آن محاسبه می‌شود، Centroid را ببینید .

وجه ها [ ویرایش ]

مجموع مساحت هر سه وجه بیشتر از مساحت وجه چهارم است. [29] : ص225، شماره 159

مشخصات وب

در این وبلاگ به ریاضیات و کاربردهای آن و تحقیقات در آنها پرداخته می شود. مطالب در این وبلاگ ترجمه سطحی و اولیه است و کامل نیست.در صورتی سوال یا نظری در زمینه ریاضیات دارید مطرح نمایید .در صورت امکان به آن می پردازم. من دوست دارم برای یافتن پاسخ به سوالات و حل پروژه های علمی با دیگران همکاری نمایم.در صورتی که شما هم بامن هم عقیده هستید با من تماس بگیرید.
09132003030

ریاضیات

آموزش ریاضی