3-تونل زنی کوانتومی

توسط علی رضا نقش نیلچی | شنبه دوم دی ۱۴۰۲ | 22:32

بحث ریاضی [ ویرایش ]

تونل زنی کوانتومی از طریق یک مانع انرژی ذره تونل شده یکسان است اما دامنه احتمال کاهش می یابد.

معادله شرودینگر [ ویرایش ]

معادله شرودینگر مستقل از زمان برای یک ذره در یک بعد می تواند به صورت نوشته شود

$-{\frac {\hbar ^{2}}{2m}}{\frac {d^{2}}{dx^{2}}}\Psi (x)+V(x)\Psi ( x)=E\Psi (x)$ یا

${\frac {d^{2}}{dx^{2}}}\Psi (x)={\frac {2m}{\hbar ^{2}}}\left(V(x)- E\right)\Psi (x)\equiv {\frac {2m}{\hbar ^{2}}}M(x)\Psi (x)،$

جایی که

$\hbar$ ثابت پلانک کاهش یافته است ،
m جرم ذره است،
x نشان دهنده فاصله اندازه گیری شده در جهت حرکت ذره است،
Ψ تابع موج شرودینگر است،
V انرژی پتانسیل ذره است (نسبت به هر سطح مرجع مناسب اندازه گیری می شود)
E انرژی ذره ای است که با حرکت در محور x مرتبط است (نسبت به V اندازه گیری می شود ).
M ( x ) کمیتی است که با V ( x ) - E تعریف می شود که در فیزیک نام پذیرفته شده ای ندارد.

جواب های معادله شرودینگر برای مقادیر مختلف x ، بسته به مثبت یا منفی بودن M ( x ) اشکال متفاوتی دارند. هنگامی که M ( x ) ثابت و منفی است، می توان معادله شرودینگر را به شکل نوشت

${\frac {d^{2}}{dx^{2}}}\Psi (x)={\frac {2m}{\hbar ^{2}}}M(x)\Psi (x )=-k^{2}\Psi (x),\qquad {\text{where}}\quad k^{2}=-{\frac {2m}{\hbar ^{2}}}M.$

جواب های این معادله نشان دهنده امواج متحرک با فاز ثابت + k یا - k هستند . از طرف دیگر، اگر M ( x ) ثابت و مثبت باشد، معادله شرودینگر را می توان به شکل نوشتاری

${\frac {d^{2}}{dx^{2}}}\Psi (x)={\frac {2m}{\hbar ^{2}}}M(x)\Psi (x )={\kappa }^{2}\Psi (x),\qquad {\text{where}}\quad {\kappa }^{2}={\frac {2m}{\hbar ^{2}} }M.$

راه حل های این معادله افزایش و نزول نمایی به صورت امواج فزاینده است . وقتی M ( x ) با موقعیت تغییر می کند، بسته به منفی یا مثبت بودن M(x) همان تفاوت در رفتار رخ می دهد. نتیجه این است که علامت M ( x ) ماهیت محیط را تعیین می کند، با M(x) منفی مربوط به محیط A و M ( x ) مثبت مربوط به محیط B است. بنابراین نتیجه می شود که جفت شدن موج فزاینده می تواند اتفاق بیفتد اگر یک ناحیه وجود داشته باشد. M ( x ) مثبت بین دو ناحیه M منفی ( x ) قرار می گیرد ، از این رو یک مانع بالقوه ایجاد می کند.

ریاضیات برخورد با موقعیتی که در آن M ( x ) با x تغییر می کند دشوار است، مگر در موارد خاص که معمولاً با حقیقیت فیزیکی مطابقت ندارد. یک درمان کامل ریاضی در تک نگاری فرومن و فرومن در سال 1965 آمده است. ایده های آنها در کتاب های درسی فیزیک گنجانده نشده است، اما تصحیحات آنها تأثیر کمی دارد.

تقریب WKB [ ویرایش ]

مقاله اصلی: تقریب WKB

تابع موج به صورت نمایی یک تابع بیان می شود:

$\Psi (x)=e^{\Phi (x)}،$ جایی که

$\Phi ''(x)+\Phi '(x)^{2}={\frac {2m}{\hbar ^{2}}}\left(V(x)-E\right).$

$\Phi'(x)$ سپس به دو بخش حقیقی و موهومی تقسیم می شود:

$\Phi '(x)=A(x)+iB(x),$ که در آن A ( x ) و B ( x ) توابع با ارزش حقیقی هستند.

جایگزینی معادله دوم به معادله اول و استفاده از این حقیقیت که قسمت حقیقی باید 0 باشد، نتیجه می شود:

$A'(x)+A(x)^{2}-B(x)^{2}={\frac {2m}{\hbar ^{2}}}\left(V(x)- E\راست).$

مدت زمان: 11 ثانیه.0:11

تونل زنی کوانتومی در فرمول فضای فازی مکانیک کوانتومی. عملکرد ویگنر برای تونل زدن از طریق مانع بالقوه $U(x)=8e^{-0.25x^{2}}$ در واحدهای اتمی (au). خطوط یکپارچه نشان دهنده مجموعه سطح همیلتونی است $H(x,p) = p^2 / 2 + U(x)$ .

برای حل این معادله با استفاده از تقریب نیمه کلاسیک، هر تابع باید به عنوان یک سری توانی در $\hbar$ . از معادلات، سری توان باید حداقل با یک مرتبه شروع شود $\hbar^{-1}$ برای ارضای بخش حقیقی معادله؛ برای یک حد کلاسیک خوب که با بالاترین توان ثابت پلانک شروع می شود ترجیح داده می شود که منجر به

$A(x)={\frac {1}{\hbar }}\sum _{k=0}^{\infty }\hbar ^{k}A_{k}(x)$ و

$B(x)={\frac {1}{\hbar }}\sum _{k=0}^{\infty }\hbar ^{k}B_{k}(x)،$

با محدودیت های زیر در پایین ترین شرایط،

$A_{0}(x)^{2}-B_{0}(x)^{2}=2m\left(V(x)-E\right)$ و

$A_{0}(x)B_{0}(x)=0.$

در این مرحله دو حالت شدید را می توان در نظر گرفت.

مورد 1

اگر دامنه در مقایسه با فاز به کندی تغییر کند $A_0(x) = 0$ و

$B_{0}(x)=\pm {\sqrt {2m\left(EV(x)\right)}}$ که با حرکت کلاسیک مطابقت دارد. حل کردن ترتیب بعدی بازدهی توسعه

$\Psi (x)\approx C{\frac {e^{i\int dx{\sqrt {{\frac {2m}{\hbar ^{2}}}\left(EV(x)\right )}}+\theta }}{\sqrt[{4}]{{\frac {2m}{\hbar ^{2}}}\left(EV(x)\right)}}}$

مورد 2

اگر فاز در مقایسه با دامنه به کندی تغییر کند، $B_0 (x) = 0$ و

$A_{0}(x)=\pm {\sqrt {2m\left(V(x)-E\right)}}$ که مربوط به تونل زنی است. حل کردن ترتیب بعدی بازدهی توسعه

$\Psi (x)\approx {\frac {C_{+}e^{+\int dx{\sqrt {{\frac {2m}{\hbar ^{2}}}\left(V(x )-E\right)}}}+C_{-}e^{-\int dx{\sqrt {{\frac {2m}{\hbar ^{2}}}\left(V(x)-E\ راست)}}}}{\sqrt[{4}]{{\frac {2m}{\hbar ^{2}}}\left(V(x)-E\right)}}}$

در هر دو مورد، از مخرج آشکار است که هر دو این راه حل تقریبی در نزدیکی نقاط عطف کلاسیک بد هستند. $E = V(x)$ . دور از تپه بالقوه، ذره شبیه به یک موج آزاد و نوسانی عمل می کند. در زیر تپه بالقوه، ذره دستخوش تغییرات نمایی در دامنه می شود. با در نظر گرفتن رفتار در این محدوده ها و نقاط عطف کلاسیک می توان یک راه حل جهانی ایجاد کرد.

برای شروع، یک نقطه عطف کلاسیک، $x_{1}$ انتخاب شده است و $\frac{2m}{\hbar^2}\left(V(x)-E\right)$ در یک سری توانی در $x_{1}$ گسترش یافته است:

${\frac {2m}{\hbar ^{2}}}\left(V(x)-E\right)=v_{1}(x-x_{1})+v_{2}(x -x_{1})^{2}+\cdots$

حفظ فقط عبارت مرتبه اول خطی بودن را تضمین می کند:

${\frac {2m}{\hbar ^{2}}}\left(V(x)-E\right)=v_{1}(x-x_{1}).$

با استفاده از این تقریب، معادله نزدیک است $x_{1}$ تبدیل به یک معادله دیفرانسیل می شود :

${\frac {d^{2}}{dx^{2}}}\Psi (x)=v_{1}(x-x_{1})\Psi (x).$

این را می توان با استفاده از توابع ایری به عنوان راه حل حل کرد.

$\Psi (x)=C_{A}Ai\left({\sqrt[{3}]{v_{1}}}(x-x_{1})\right)+C_{B}Bi\ چپ({\sqrt[{3}]{v_{1}}}(x-x_{1})\راست)$

با در نظر گرفتن این راه حل ها برای تمام نقاط عطف کلاسیک، یک راه حل جهانی می تواند تشکیل شود که راه حل های محدود کننده را به هم پیوند می دهد. با توجه به دو ضریب در یک طرف یک نقطه عطف کلاسیک، دو ضریب در طرف دیگر یک نقطه عطف کلاسیک را می توان با استفاده از این راه حل محلی برای اتصال آنها تعیین کرد.

از این رو، راه حل های تابع ایری به توابع سینوس، کسینوس و نمایی در حدود مناسب مجانبی خواهند بود. روابط بین، $سی، تتا$ و $C_{+}،C_{-}$ هستند

$C_{+}={\frac {1}{2}}C\cos {\left(\theta -{\frac {\pi }{4}}\right)}$ و

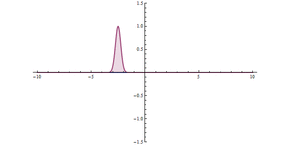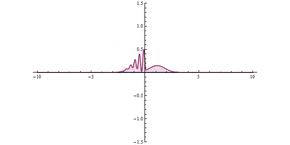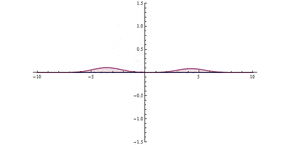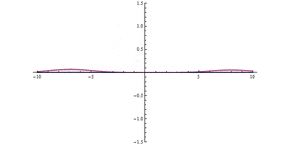
تونل زنی کوانتومی از طریق یک مانع در مبدا ( x = 0)، یک مانع بالقوه بسیار بالا، اما باریک وجود دارد. اثر تونل زنی قابل توجهی را می توان مشاهده کرد.

$C_{-} = - C \sin{\left(\theta - \frac{\pi}{4}\right)}$

با ضرایب یافت شده می توان راه حل کلی را پیدا کرد. بنابراین، ضریب انتقال برای یک تونل ذرات از طریق یک مانع پتانسیل منفرد است

$T(E)=e^{-2\int _{x_{1}}^{x_{2}}dx{\sqrt {{\frac {2m}{\hbar ^{2}}}\ چپ[V(x)-E\right]}}}،$

جایی که، $x_1، x_2$ دو نقطه عطف کلاسیک برای مانع بالقوه هستند.

برای یک مانع مستطیلی، این عبارت ساده می شود:

$T(E)=e^{-2{\sqrt {{\frac {2m}{\hbar ^{2}}}(V_{0}-E)}}(x_{2}-x_{ 1})}.$

سریعتر از نور [ ویرایش ]

همچنین ببینید: سریعتر از نور

برخی از فیزیکدانان ادعا کرده اند که ممکن است ذرات اسپین صفر در هنگام تونل زدن سریعتر از سرعت نور حرکت کنند . [8] به نظر می‌رسد که این امر اصل علیت را نقض می‌کند ، زیرا چارچوب مرجعی وجود دارد که در آن ذره قبل از خروج می‌رسد. در سال 1998، فرانسیس ای لو به طور خلاصه پدیده تونل زنی در زمان صفر را بررسی کرد. [37] اخیراً، داده های آزمایشی زمان تونل زنی فونون ها ، فوتون ها و الکترون ها توسط گونتر نیمتز منتشر شده است . [38]

فیزیکدانان دیگر، مانند هربرت وینفول ، [39] این ادعاها را رد کردند. وینفول استدلال کرد که بسته موج یک ذره تونل زنی به صورت محلی منتشر می شود، بنابراین یک ذره نمی تواند به صورت غیر محلی از مانع عبور کند. وینفول همچنین استدلال کرد که آزمایش‌هایی که ظاهراً انتشار غیرمحلی را نشان می‌دهند اشتباه تفسیر شده‌اند. به طور خاص، سرعت گروهی یک بسته موج، سرعت آن را اندازه گیری نمی کند، بلکه به مدت زمانی که بسته موج در مانع ذخیره می شود، مرتبط است. اما مسئله این است که تابع موج همچنان در تمام نقاط به طور همزمان در داخل مانع افزایش می یابد. به عبارت دیگر، در هر منطقه ای که قابل اندازه گیری نباشد، انتشار غیرمحلی هنوز از نظر ریاضی قطعی است.

آزمایشی در سال 2020، تحت نظارت Aephraim M. Steinberg ، نشان داد که ذرات باید بتوانند با سرعت‌های ظاهری سریع‌تر از نور تونل بزنند. [40] [41]

تونل زنی دینامیکی [ ویرایش ]

نوسانات احتمالی تونل زنی کوانتومی در یک چاه مضاعف پتانسیل یکپارچه، دیده شده در فضای فاز

مفهوم تونل زنی کوانتومی را می توان به موقعیت هایی تعمیم داد که در آن یک انتقال کوانتومی بین مناطقی وجود دارد که به طور کلاسیک به هم متصل نیستند، حتی اگر هیچ مانع پتانسیل مرتبطی وجود نداشته باشد. این پدیده به تونل زنی دینامیکی معروف است. [42] [43]

تونل سازی در فضای فاز [ ویرایش ]

مفهوم تونل زنی دینامیکی به ویژه برای پرداختن به مسئله تونل زنی کوانتومی در ابعاد بالا مناسب است (d>1). در مورد یک سیستم یکپارچه ، که در آن مسیرهای کلاسیک محدود به توری در فضای فاز محدود می شوند ، تونل زنی را می توان به عنوان انتقال کوانتومی بین حالت های نیمه کلاسیک ساخته شده بر روی دو توری متمایز اما متقارن درک کرد. [44]

تونل سازی به کمک آشوب [ ویرایش ]

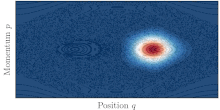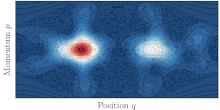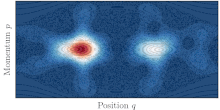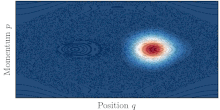
نوسانات تونل زنی به کمک هرج و مرج بین دو توری منظم که در یک دریای پر هرج و مرج جاسازی شده اند، در فضای فاز دیده می شوند.

در زندگی حقیقی، بیشتر سیستم ها یکپارچه نیستند و درجات مختلفی از هرج و مرج را نشان می دهند. سپس گفته می شود که دینامیک کلاسیک مخلوط است و فضای فاز سیستم معمولاً از جزایر مدارهای منظم تشکیل شده است که توسط دریای بزرگی از مدارهای آشفته احاطه شده اند. وجود دریای پر هرج و مرج، جایی که حمل و نقل به طور کلاسیک مجاز است، بین دو توری متقارن، به تونل کوانتومی بین آنها کمک می کند. این پدیده به عنوان تونل زنی به کمک آشوب شناخته می شود. [45] و با رزونانس های شدید نرخ تونل زنی در هنگام تغییر هر پارامتر سیستم مشخص می شود.

تونل زنی به کمک تشدید [ ویرایش ]

چه زمانی $\hbar$ در مقابل اندازه جزایر منظم کوچک است، ساختار ظریف فضای فاز کلاسیک نقش کلیدی در تونل‌زنی دارد. به طور خاص، دو توری متقارن "از طریق یک توالی از انتقال های کلاسیک ممنوع در سراسر تشدید غیرخطی" در اطراف دو جزیره جفت می شوند. [46]

پدیده های مرتبط [ ویرایش ]

چندین پدیده رفتاری مشابه تونل زنی کوانتومی دارند و می توان آنها را با تونل زنی به دقت توصیف کرد. مثال‌ها عبارتند از تونل‌سازی یک ارتباط کلاسیک موج-ذره، [47] جفت شدن موج فزاینده (کاربرد معادله موج ماکسول برای نور ) و استفاده از معادله موج غیر پراکنده از آکوستیک اعمال شده به "امواج روی رشته‌ها" . تا همین اواخر، کوپلینگ موج فزاینده تنها در مکانیک کوانتومی "تونل زنی" نامیده می شد. اکنون در زمینه های دیگر استفاده می شود.

این اثرات به طور مشابه با مانع پتانسیل مستطیلی مدل سازی شده اند . در این موارد، یک رسانه انتقال که از طریق آن موج از طریق آن منتشر می شود که در سرتاسر یکسان یا تقریباً یکسان است، و رسانه دوم که موج از طریق آن به طور متفاوتی حرکت می کند. این را می توان به عنوان یک ناحیه نازک از محیط B بین دو ناحیه از محیط A توصیف کرد. تجزیه و تحلیل یک مانع مستطیلی با استفاده از معادله شرودینگر را می توان با این اثرات دیگر تطبیق داد، مشروط بر اینکه معادله موج دارای راه حل های موج سیار در محیط A باشد اما راه حل های نمایی حقیقی در محیط B.

در اپتیک ، محیط A خلاء است در حالی که محیط B شیشه است. در آکوستیک، محیط A ممکن است مایع یا گاز و محیط B جامد باشد. برای هر دو مورد، محیط A ناحیه ای از فضا است که انرژی کل ذره بیشتر از انرژی پتانسیل آن است و محیط B مانع پتانسیل است. اینها یک موج ورودی و امواج حاصل در هر دو جهت دارند. ممکن است رسانه ها و موانع بیشتری وجود داشته باشد و نیازی نیست که موانع مجزا باشند. تقریب ها در این مورد مفید هستند.

همچنین ببینید [ ویرایش ]

تخلیه سد دی الکتریک
انتشار الکترون میدانی
روش هلشتاین – شاه ماهی
تونل زنی پروتون
شبیه سازی کوانتومی
تقاطع تونل ابررسانا
دیود تونل
تقاطع تونل
سفید چاله

https://en.wikipedia.org/wiki/Quantum_tunnelling

مشخصات وب

در این وبلاگ به ریاضیات و کاربردهای آن و تحقیقات در آنها پرداخته می شود. مطالب در این وبلاگ ترجمه سطحی و اولیه است و کامل نیست.در صورتی سوال یا نظری در زمینه ریاضیات دارید مطرح نمایید .در صورت امکان به آن می پردازم. من دوست دارم برای یافتن پاسخ به سوالات و حل پروژه های علمی با دیگران همکاری نمایم.در صورتی که شما هم بامن هم عقیده هستید با من تماس بگیرید.
09132003030

ریاضیات

آموزش ریاضی