1-نمودار جریان سیگنال

توسط علی رضا نقش نیلچی | دوشنبه یکم خرداد ۱۴۰۲ | 17:49

از ویکیپدیا، دانشنامه آزاد

"گراف میسون" به اینجا هدایت می شود. برای سایر نمودارهای جریان، نمودار جریان (ریاضیات) را ببینید .

نمودار جریان سیگنال یا نمودار جریان سیگنال ( SFG )، که توسط کلود شانون اختراع شد ، [1] ، اما اغلب به نام ساموئل جفرسون میسون که این اصطلاح را ابداع کرد، نمودار میسون نامیده می‌شود، [2] یک نمودار جریان تخصصی است ، یک نمودار جهت‌دار که در آن گره ها متغیرهای سیستم را نشان می دهند و شاخه ها (لبه ها، کمان ها یا فلش ها) نشان دهنده ارتباطات عملکردی بین جفت گره ها هستند. بنابراین، نظریه گراف جریان سیگنال مبتنی بر نظریه گراف های جهت دار ( که دیگراف نیز نامیده می شود)، که شامل گراف های جهت دار نیز می شود.. این نظریه ریاضی نمودارها البته کاملا جدا از کاربردهای آن وجود دارد. [3] [4]

SFG ها بیشتر برای نمایش جریان سیگنال در یک سیستم فیزیکی و کنترل کننده(های) آن استفاده می شوند که یک سیستم فیزیکی-سایبری را تشکیل می دهند . از دیگر کاربردهای آنها می توان به نمایش جریان سیگنال در شبکه های مختلف الکترونیکی و تقویت کننده ها، فیلترهای دیجیتال ، فیلترهای متغیر حالت و برخی دیگر از انواع فیلترهای آنالوگ اشاره کرد. تقریباً در تمام ادبیات، نمودار جریان سیگنال با مجموعه ای از معادلات خطی مرتبط است .

تاریخچه [ ویرایش ]

وای-کای چن نوشت: "مفهوم نمودار جریان سیگنال در اصل توسط شانون [1942] [1] در برخورد با کامپیوترهای آنالوگ به کار گرفته شد. بیشترین اعتبار برای فرمول بندی نمودارهای جریان سیگنال معمولاً به میسون تعلق می گیرد . 1953، [2] [1956] [5] او نشان داد که چگونه می توان از تکنیک نمودار جریان سیگنال برای حل برخی از مسائل الکترونیکی دشوار به روشی نسبتاً ساده استفاده کرد.اصطلاح نمودار جریان سیگنال به دلیل کاربرد اصلی آن در الکترونیک استفاده شد. مشکلات و ارتباط با سیگنال های الکترونیکی و نمودارهای جریان سیستم های مورد مطالعه." [6]

لورنز نوشت: "قبل از کار میسون ، سی شانون [1] تعدادی از خصوصیات آنچه که امروزه به عنوان نمودار جریان شناخته می شود را بررسی کرد. متأسفانه، مقاله در ابتدا طبقه بندی محدودی داشت و افراد بسیار کمی به مواد دسترسی داشتند. " [7]

"قوانین ارزیابی گراف تعیین کننده نمودار میسون برای اولین بار توسط شانون [1942] با استفاده از استقرای ریاضی ارائه و اثبات شد. کار او اساساً ناشناخته باقی ماند حتی پس از اینکه میسون کار کلاسیک خود را در سال 1953 منتشر کرد. سه سال بعد، میسون [1956] ] قواعد را دوباره کشف کرد و با در نظر گرفتن مقدار یک تعیین کننده و نحوه تغییر آن با اضافه شدن متغیرها به نمودار آنها را اثبات کرد. [...]» [8]

دامنه برنامه [ ویرایش ]

Robichaud و همکاران دامنه کاربرد SFG ها را به شرح زیر شناسایی کنید: [9]

"همه سیستم های فیزیکی مشابه این شبکه ها [ساخته شده از ترانسفورماتورهای ایده آل، عناصر فعال و ژیراتورها] حوزه کاربرد تکنیک های توسعه یافته [اینجا] را تشکیل می دهند. ترنت [10] نشان داده است که تمام سیستم های فیزیکی که شرایط زیر را برآورده می کنند، سقوط می کنند. در این دسته

سیستم یکپارچه محدود از تعدادی قسمت ساده تشکیل شده است که هر یک از آنها دارای خواص دینامیکی شناخته شده ای هستند که با استفاده از دو نوع متغیر اسکالر و پارامترهای سیستم می توان آنها را با معادلات تعریف کرد. متغیرهای نوع اول مقادیری را نشان می دهند که می توان آنها را حداقل به صورت مفهومی با اتصال یک ابزار نشانگر به دو نقطه اتصال عنصر اندازه گیری کرد. متغیرهای نوع دوم مقادیری را مشخص می کنند که با اتصال یک متر به صورت سری به عنصر قابل اندازه گیری هستند. سرعت‌ها و موقعیت‌های نسبی، اختلاف فشار و ولتاژ کمیت‌های معمولی کلاس اول هستند، در حالی که جریان‌های الکتریکی، نیروها، نرخ‌های جریان گرما، متغیرهای نوع دوم هستند. Firestone اولین کسی است که این دو نوع متغیر را با نام بین متغیرها تشخیص داده استو از طریق متغیرها .
متغیرهای نوع اول باید از قانون مش، مشابه قانون ولتاژ کیرشهوف تبعیت کنند، در حالی که متغیرهای نوع دوم باید قانون وقوع مشابه با قانون فعلی کیرشهوف را برآورده کنند.
ابعاد فیزیکی محصولات مناسب متغیرهای این دو نوع باید سازگار باشد. برای سیستم‌هایی که این شرایط در آنها برآورده می‌شود، می‌توان یک نمودار خطی هم‌شکل با ویژگی‌های دینامیکی سیستم همانطور که توسط متغیرهای انتخاب شده توصیف شده است ترسیم کرد. تکنیک‌های [...] را می‌توان مستقیماً در این نمودارهای خطی و همچنین در شبکه‌های الکتریکی برای به دست آوردن نمودار جریان سیگنال از سیستم اعمال کرد.»

مفاهیم اساسی نمودار جریان [ ویرایش ]

تصویر زیر و معنای آن توسط میسون برای نشان دادن مفاهیم اساسی معرفی شد: [2]

(الف) نمودار جریان ساده، (ب) فلش‌های (الف) روی گره 2 (ج) فلش‌های (الف) روی گره 3 قرار می‌گیرند.

در نمودارهای جریان ساده شکل، یک وابستگی عملکردی یک گره با یک فلش ورودی نشان داده می شود، گرهی که این تأثیر را ایجاد می کند، ابتدای این فلش است، و در کلی ترین شکل آن، نمودار جریان سیگنال تنها با فلش های ورودی نشان می دهد. گره هایی که بر پردازش در گره دریافت کننده تأثیر می گذارند، و در هر گره، i ، متغیرهای ورودی بر اساس یک تابع مرتبط با آن گره پردازش می شوند، مثلاً F i . فلوگراف در (a) مجموعه ای از روابط صریح را نشان می دهد:

${\begin{aligned}x_{{\mathrm {1}}}&={\text{یک متغیر مستقل}}\\x_{{\mathrm {2}}}&=F_{2}(x_{{\ ریاضی {1}}}، x_{{\mathrm {3}}})\\x_{{\mathrm {3}}}&=F_{3}(x_{{\mathrm {1}}}،x_{ {\mathrm {2}}},x_{{\mathrm {3}}})\\\end{تراز شده}}$

گره x 1 یک گره ایزوله است زیرا هیچ پیکانی وارد نمی شود. معادلات x 2 و x 3 دارای نمودارهایی است که در قسمت های (b) و (c) شکل نشان داده شده است.

این روابط برای هر گره تابعی را تعریف می کند که سیگنال های ورودی دریافتی را پردازش می کند. هر گره غیر منبع سیگنال های ورودی را به روشی ترکیب می کند و سیگنال حاصل را در امتداد هر شاخه خروجی پخش می کند. "گراف جریان، همانطور که در اصل توسط میسون تعریف شده است، مجموعه ای از روابط عملکردی، خطی یا غیر خطی را نشان می دهد." [9]

با این حال، گراف میسون که معمولاً استفاده می شود، محدودتر است، با این فرض که هر گره به سادگی فلش های ورودی خود را جمع می کند، و هر شاخه فقط شامل گره آغازگر درگیر می شود. بنابراین، در این رویکرد محدودتر، گره x 1 تحت تأثیر قرار نمی گیرد در حالی که:

$x_{2}=f_{{21}}(x_{1})+f_{{23}}(x_{3})$

$x_{3}=f_{{31}}(x_{1})+f_{{32}}(x_{2})+f_{{33}}(x_{3})\ ,$

و اکنون توابع f ij را می‌توان با شاخه‌های جریان سیگنال ij که به جفت گره‌های x i , x j می‌پیوندند ، به جای داشتن روابط عمومی مرتبط با هر گره، مرتبط کرد. کمک یک گره به خودش مانند f 33 برای x 3 ، حلقه self-loop نامیده می شود . غالباً این توابع صرفاً فاکتورهای ضربی هستند (اغلب به آنها انتقال یا بهره گفته می شود )، برای مثال، f ij (xj ) =c ij x j ، که در آن cیک اسکالر است، اما احتمالاً تابعی از پارامتری مانند متغیر تبدیل لاپلاس s است . نمودارهای جریان سیگنال اغلب با سیگنال های تبدیل شده به لاپلاس استفاده می شوند، زیرا آنها سیستم معادلات دیفرانسیل خطی را نشان می دهند . در این مورد، انتقال، c(s) ، اغلب تابع انتقال نامیده می شود .

انتخاب متغیرها [ ویرایش ]

به طور کلی روش های مختلفی برای انتخاب متغیرها در یک سیستم پیچیده وجود دارد. متناسب با هر انتخاب، یک سیستم معادلات را می توان نوشت و هر سیستم معادلات را می توان در یک نمودار نشان داد. این فرمول معادلات مستقیم و خودکار می‌شود اگر کسی تکنیک‌هایی را در اختیار داشته باشد که به رسم نمودار مستقیماً از نمودار شماتیک سیستم مورد مطالعه اجازه می‌دهد. ساختار نمودارهای به دست آمده به روشی ساده با توپولوژی نمودار شماتیک مرتبط است و در نظر گرفتن معادلات غیر ضروری می شود.، حتی به طور ضمنی، برای به دست آوردن نمودار. در برخی موارد، به سادگی باید نمودار جریان را در نمودار شماتیک تصور کرد و حتی بدون ترسیم نمودار جریان، می توان به پاسخ های مورد نظر دست یافت.
- Robichaud [11]

منحصر به فرد نبودن [ ویرایش ]

Robichaud و همکاران نوشت: "گراف جریان سیگنال حاوی همان اطلاعات معادلاتی است که از آن مشتق شده است؛ اما مطابقت یک به یک بین نمودار و سیستم معادلات وجود ندارد. یک سیستم نمودارهای متفاوتی را بر اساس ترتیبی که از معادلات برای تعریف متغیر نوشته شده در سمت چپ استفاده می شود." [9] اگر همه معادلات همه متغیرهای وابسته را به هم مرتبط کنند، n وجود دارد ! SFG های ممکن برای انتخاب [12]

نمودارهای خطی جریان سیگنال [ ویرایش ]

روش‌های گراف جریان سیگنال خطی (SFG) فقط برای سیستم‌های خطی تغییرناپذیر زمان اعمال می‌شوند ، همانطور که توسط تئوری مرتبط آنها مطالعه شده است . هنگام مدل‌سازی یک سیستم مورد علاقه، اولین گام اغلب تعیین معادلاتی است که عملکرد سیستم را بدون تخصیص علل و اثرات نشان می‌دهند (به این مدل‌سازی علّی گفته می‌شود). [13] سپس یک SFG از این سیستم معادلات به دست می آید.

یک SFG خطی شامل گره‌هایی است که با نقطه‌ها و شاخه‌های جهت دار وزنی که با فلش‌ها نشان داده می‌شوند. گره ها متغیرهای معادلات و وزن شاخه ها ضرایب هستند. سیگنال ها فقط می توانند از یک شاخه در جهتی عبور کنند که با فلش آن نشان داده شده است. عناصر یک SFG فقط می توانند عملیات ضرب در یک ضریب و جمع را نشان دهند که برای نشان دادن معادلات مقید کافی است. هنگامی که یک سیگنال از یک شاخه در جهت مشخص شده عبور می کند، سیگنال در وزن شاخه ضرب می شود. هنگامی که دو یا چند شاخه به یک گره هدایت می شوند، خروجی های آنها اضافه می شود.

برای سیستم هایی که با معادلات جبری خطی یا دیفرانسیل توصیف می شوند، نمودار جریان سیگنال از نظر ریاضی معادل سیستم معادلات توصیف کننده سیستم است و معادلات حاکم بر گره ها برای هر گره با جمع شاخه های ورودی به آن گره کشف می شوند. این شاخه های ورودی سهم گره های دیگر را منتقل می کنند، که به عنوان مقدار گره متصل ضرب در وزن شاخه اتصال بیان می شود، معمولاً یک عدد واقعی یا تابع برخی از پارامترها (به عنوان مثال یک متغیر تبدیل لاپلاس s ) .

برای شبکه‌های فعال خطی، Choma می‌نویسد: [14] «منظور از «نمایش جریان سیگنال» [یا «گراف»، همانطور که معمولاً به آن اشاره می‌شود] نموداری است که با نمایش روابط جبری بین متغیرهای شاخه مربوطه شبکه، تصویر واضحی از نحوه "جریان" سیگنال ورودی اعمال شده از پورت های ورودی به خروجی ترسیم می کند."

انگیزه ای برای تجزیه و تحلیل SFG توسط چن شرح داده شده است: [15]

"تحلیل یک سیستم خطی در نهایت به حل یک سیستم معادلات جبری خطی کاهش می یابد. به عنوان جایگزینی برای روش های جبری مرسوم برای حل سیستم، می توان با در نظر گرفتن خواص گراف های جهت دار خاص مرتبط با سیستم." [به بخش فرعی مراجعه کنید: حل معادلات خطی .] "معلومات معادلات با گره های نمودار مطابقت دارند، در حالی که روابط خطی بین آنها به شکل لبه های جهت دار ظاهر می شوند که گره ها را به هم متصل می کنند. ... نمودارهای جهت دار مرتبط در بسیاری از موارد می توان مستقیماً با بازرسی سیستم فیزیکی بدون نیاز به فرمول → معادلات مرتبط تنظیم کرد.

اجزای اصلی [ ویرایش ]

عناصر و ساختارهای یک نمودار جریان سیگنال.

یک نمودار جریان سیگنال خطی مربوط به سیستمی از معادلات خطی [16] به شکل زیر است:

${\begin{aligned}x_{{\mathrm {j}}}&=\sum _{{{\mathrm {k}}=1}}^{{{\mathrm {N}}}}t_{{\ mathrm {jk}}}x_{{\mathrm {k}}}\end{تراز شده}}$

جایی که $t_{{jk}}$ = انتقال (یا کسب) ازایکسک $x_{k}$ ب $x_{j}$ .

شکل سمت راست عناصر و ساختارهای مختلف یک نمودار جریان سیگنال (SFG) را نشان می دهد. [17]

نمایش (الف) یک گره است. در این مورد، گره برچسب گذاری می شودایکس $ایکس$ . گره یک راس است که یک متغیر یا سیگنال را نشان می دهد.

یک گره منبع فقط شاخه های خروجی دارد (نماینده یک متغیر مستقل). به عنوان یک مورد خاص، یک گره ورودی با داشتن یک یا چند فلش متصل به سمت گره و هیچ فلشی به سمت گره مشخص می شود. هر SFG باز و کامل حداقل یک گره ورودی خواهد داشت.

یک گره خروجی یا سینک فقط شاخه های ورودی دارد (نماینده یک متغیر وابسته). اگرچه هر گره ای می تواند یک خروجی باشد، گره های خروجی صریح اغلب برای ارائه وضوح استفاده می شوند. گره های خروجی صریح با داشتن یک یا چند فلش متصل به گره و هیچ فلشی به سمت گره مشخص می شوند. گره های خروجی صریح مورد نیاز نیستند.

یک گره مختلط دارای هر دو شاخه ورودی و خروجی است.

شکل (ب) شاخه ای با بهره ضربی استمتر $متر$ . معنی این است که خروجی، در نوک فلش، استمتر $متر$ برابر ورودی دم فلش. بهره می تواند یک ثابت ساده یا یک تابع باشد (به عنوان مثال: تابعی از یک متغیر تبدیل مانندس $س$ ، $\ امگا$ ، یا $z$ ، برای روابط لاپلاس، فوریه یا تبدیل Z).

شکل (ج) شاخه ای است با بهره ضربی یک. هنگامی که سود حذف می شود، وحدت فرض می شود.

نمایشگاه (د) $V_{in}$ یک گره ورودی است. در این مورد، $V_{in}$ در سود ضرب می شود $متر$ .

نمایشگاه (ه) $من_{{بیرون}}$ یک گره خروجی صریح است. لبه ورودی دارای سود است $متر$ .

نمایش (f) جمع را نشان می دهد. هنگامی که دو یا چند فلش به سمت یک گره اشاره می کنند، سیگنال های حمل شده توسط لبه ها اضافه می شوند.

شکل (g) یک حلقه ساده را نشان می دهد. بهره حلقه است $A\ بار m$ .

شکل (h) بیان را نشان می دهد $Z=aX+bY$ .

اصطلاحات مورد استفاده در نظریه خطی SFG نیز عبارتند از: [17]

مسیر. یک مسیر مجموعه ای پیوسته از شاخه ها است که در جهتی که با فلش های شاخه نشان داده شده است طی می شود.
- مسیر باز اگر هیچ گره ای دوباره بازدید نشود، مسیر باز است.
- مسیر رو به جلو. مسیری از یک گره ورودی (منبع) به یک گره خروجی (سینک) که هیچ گرهی را مجدداً بازدید نمی کند.
بهره ی مسیر : حاصل حاصل از دستاوردهای همه ی شاخه های مسیر.
حلقه. یک مسیر بسته (از همان گره منشا می گیرد و به پایان می رسد و هیچ گره ای بیش از یک بار لمس نمی شود).
بهره حلقه : حاصلضرب حاصل از تمام شاخه های حلقه.
حلقه های غیر لمسی حلقه های غیر لمسی هیچ گره مشترکی ندارند.
کاهش نمودار حذف یک یا چند گره از یک گراف با استفاده از تبدیل گراف.
- گره باقیمانده در هر فرآیند کاهش گراف در نظر گرفته شده، گره هایی که در نمودار جدید حفظ می شوند، گره های باقی مانده نامیده می شوند. [2]
تقسیم یک گره تقسیم یک گره مربوط به تقسیم یک گره به دو نیمه گره است که یکی سینک و دیگری منبع است. [18]
Index : شاخص یک گراف حداقل تعداد گره هایی است که باید برای حذف تمام حلقه های یک گراف تقسیم شوند.
- گره شاخص. گره هایی که برای تعیین شاخص یک نمودار تقسیم می شوند، گره های شاخص نامیده می شوند و به طور کلی منحصر به فرد نیستند.

کاهش سیستماتیک به منابع و سینک ها [ ویرایش ]

یک نمودار جریان سیگنال ممکن است با قوانین تبدیل گراف ساده شود. [19] [20] [21] به این قوانین ساده‌سازی به عنوان جبر نمودار جریان سیگنال نیز گفته می‌شود . [22] هدف از این کاهش، مرتبط کردن متغیرهای وابسته مورد علاقه (گره‌های باقی‌مانده، سینک‌ها) به متغیرهای مستقل آن (منابع) است.

کاهش سیستماتیک یک نمودار خطی سیگنال جریان یک روش گرافیکی معادل روش حذف گاوس-جردن برای حل معادلات خطی است. [23]

قوانین ارائه شده در زیر ممکن است بارها و بارها اعمال شوند تا زمانی که نمودار جریان سیگنال به "حداقل شکل باقیمانده" کاهش یابد. کاهش بیشتر می تواند به حذف حلقه یا استفاده از "فرمول کاهش" با هدف اتصال مستقیم گره های سینک که نشان دهنده متغیرهای وابسته به گره های مبدا نشان دهنده متغیرهای مستقل است نیاز داشته باشد. با این ابزار، هر نمودار جریان سیگنال را می توان با حذف متوالی گره های داخلی ساده کرد تا زمانی که فقط گره های ورودی و خروجی و شاخص باقی بمانند. [24] [25] Robichaud این فرآیند کاهش سیستماتیک نمودار جریان را شرح داد:

کاهش یک گراف با حذف گره های خاص برای به دست آوردن یک نمودار باقیمانده که فقط متغیرهای مورد علاقه را نشان می دهد، انجام می شود. این حذف گره ها " جذب گره " نامیده می شود". این روش به فرآیند آشنای حذف متوالی متغیرهای نامطلوب در یک سیستم معادلات نزدیک است. می توان با حذف گره مربوطه در نمودار یک متغیر را حذف کرد. اگر نمودار را به اندازه کافی کاهش داد، می توان به جواب رسید. برای هر متغیر و این هدفی است که در این توصیف روش های مختلف کاهش نمودار در نظر گرفته می شود.اما در عمل، تکنیک های کاهش صرفاً برای تبدیل نمودار به یک گراف باقیمانده استفاده می شود که مقداری را بیان می کند. راه حل های کامل با اعمال قانون میسون راحت تر به دست می آیند . [26] خود نمودار فرآیند کاهش را برنامه ریزی می کند. در واقع یک بازرسی ساده از نمودار به آسانی مراحل مختلف کاهش را نشان می‌دهد که با تبدیل‌های ابتدایی، حذف حلقه، یا با استفاده از فرمول کاهش انجام می‌شوند. [26]
- Robichaud، نمودارهای جریان سیگنال و کاربردها، 1962

برای کاهش دیجیتالی یک نمودار جریان با استفاده از یک الگوریتم، Robichaud مفهوم یک نمودار جریان ساده را به یک نمودار جریان تعمیم یافته گسترش می دهد:

قبل از تشریح فرآیند کاهش ... مطابقت بین نمودار و سیستم معادلات خطی ... باید تعمیم داده شود ... نمودارهای تعمیم یافته برخی از روابط عملیاتی بین گروه های متغیر را نشان می دهند ... به هر شاخه از تعمیم یافته گراف با ماتریسی مرتبط است که روابط بین متغیرهای نشان داده شده توسط گره‌های انتهای آن شاخه را نشان می‌دهد... [27] تبدیل‌های ابتدایی [که توسط Robichaud در شکل 7.2، ص. 184] و کاهش حلقه اجازه حذف هر گره j از نمودار را با فرمول کاهش می دهد.:[در معادله Robichaud's 7-1 توضیح داده شده است]. با فرمول کاهش، همیشه امکان کاهش یک نمودار با هر ترتیبی وجود دارد... [پس از کاهش] نمودار نهایی یک گراف آبشاری خواهد بود که در آن متغیرهای گره های سینک به صراحت به عنوان توابع منابع بیان می شوند. این تنها روش برای کاهش گراف تعمیم یافته است زیرا قانون میسون به وضوح قابل اجرا نیست. [28]
- Robichaud، نمودارهای جریان سیگنال و کاربردها، 1962

تعریف تحول ابتدایی از نویسنده ای به نویسنده دیگر متفاوت است:

برخی از نویسندگان فقط جمع سودهای لبه های موازی و ضرب سودهای لبه سری را تبدیل های اولیه می دانند، اما حذف حلقه های خود را [23] [29] در نظر نمی گیرند.
سایر نویسندگان حذف حلقه خود را یک دگرگونی ابتدایی می دانند [30]

لبه های موازی لبه های موازی را با یک لبه با بهره ای برابر با مجموع بهره های اولیه جایگزین کنید.

نمودار سمت چپ دارای لبه های موازی بین گره ها است. در سمت راست، این لبه‌های موازی با یک یال منفرد جایگزین شده‌اند که بهره‌ای برابر با مجموع بهره‌های هر یال اصلی دارد.

معادلات مربوط به کاهش بین N و گره I 1 عبارتند از:

${\begin{aligned}N&=I_{{\mathrm {1}}}f_{{\mathrm {1}}}+I_{{\mathrm {1}}}f_{{\mathrm {2}}}+ من f_{{\mathrm {2}}}+f_{{\mathrm {3}}})+...\\\end{تراز شده}}$

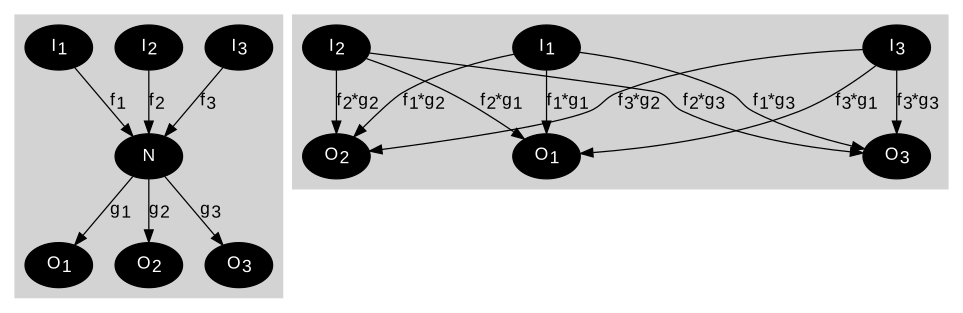
لبه های خروجی لبه های خروجی را با لبه هایی که مستقیماً از منابع گره جاری می شوند جایگزین کنید.

گراف سمت چپ دارای یک گره میانی N بین گره هایی است که از آنها جریان دارد و گره هایی که به آنها جریان می یابد. نمودار سمت راست جریان های مستقیم بین این مجموعه گره ها را بدون عبور از N نشان می دهد .

برای سادگی، N و جریان های ورودی آن نشان داده نمی شوند. خروجی های N حذف می شوند.

معادلات مربوط به کاهش که مستقیماً سیگنال های ورودی N به سیگنال های خروجی آن مربوط می شود:

${\begin{aligned}N&=I_{{\mathrm {1}}}f_{{\mathrm {1}}}+I_{{\mathrm {2}}}f_{{\mathrm {2}}}+ من \mathrm {2}}}&=g_{{\mathrm {2}}}N\\O_{{\mathrm {3}}}&=g_{{\mathrm {3}}}N\\O_{{ \mathrm {1}}}&=g_{{\mathrm {1}}}(I_{{\mathrm {1}}}f_{{\mathrm {1}}}+I_{{\mathrm {2}} }f_{{\mathrm {2}}}+I_{{\mathrm {3}}}f_{{\mathrm {3}}})\\O_{{\mathrm {2}}}&=g_{{ \mathrm {2}}}(I_{{\mathrm {1}}}f_{{\mathrm {1}}}+I_{{\mathrm {2}}}f_{{\mathrm {2}}}+ من mathrm {1}}}f_{{\mathrm {1}}}+I_{{\mathrm {2}}}f_{{\mathrm {2}}}+I_{{\mathrm {3}}}f_{ {\mathrm {3}}})\\O_{{\mathrm {1}}}&=I_{{\mathrm {1}}}f_{{\mathrm {1}}}g_{{\mathrm {1}}}+I_{{\mathrm {2}}}f_{{\mathrm {2} }}g_{{\mathrm {1}}}+I_{{\mathrm {3}}}f_{{\mathrm {3}}}g_{{\mathrm {1}}}\\O_{{\mathrm {2}}}&=I_{{\mathrm {1}}}f_{{\mathrm {1}}}g_{{\mathrm {2}}}+I_{{\mathrm {2}}}f_{ {\mathrm {2}}}g_{{\mathrm {2}}}+I_{{\mathrm {3}}}f_{{\mathrm {3}}}g_{{\mathrm {2}}}\ \O_{{\mathrm {3}}}&=I_{{\mathrm {1}}}f_{{\mathrm {1}}}g_{{\mathrm {3}}}+I_{{\mathrm { 2}}}f_{{\mathrm {2}}}g_{{\mathrm {3}}}+I_{{\mathrm {3}}}f_{{\mathrm {3}}}g_{{\mathrm {3}}\\\end{تراز شده}}=I_{{\mathrm {1}}}f_{{\mathrm {1}}}g_{{\mathrm {3}}}+I_{{\mathrm {2}}}f_{{\mathrm {2} }}g_{{\mathrm {3}}}+I_{{\mathrm {3}}}f_{{\mathrm {3}}}g_{{\mathrm {3}}}\\\end{تراز شده} }=I_{{\mathrm {1}}}f_{{\mathrm {1}}}g_{{\mathrm {3}}}+I_{{\mathrm {2}}}f_{{\mathrm {2} }}g_{{\mathrm {3}}}+I_{{\mathrm {3}}}f_{{\mathrm {3}}}g_{{\mathrm {3}}}\\\end{تراز شده} }$

گره های سیگنال صفر

لبه های خروجی را از یک گره که مقدار آن صفر است حذف کنید.

اگر مقدار یک گره صفر باشد، می توان لبه های خروجی آن را حذف کرد.

گره های بدون خروجی

حذف یک گره بدون خروجی.

در این مورد، N یک متغیر مورد علاقه نیست، و هیچ لبه خروجی ندارد. بنابراین، N و لبه های ورودی آن را می توان حذف کرد.

لبه خود حلقه ای. لبه های حلقه را با تنظیم سود در لبه های ورودی جایگزین کنید.

نمودار سمت چپ دارای یک لبه حلقه ای در گره N با بهره g است . در سمت راست، لبه حلقه حذف شده است، و تمام لبه های ورودی تقسیم بر (1-g) هستند .

معادلات مربوط به کاهش بین N و تمام سیگنال های ورودی آن عبارتند از:

${\begin{aligned}N&=I_{{\mathrm {1}}}f_{{\mathrm {1}}}+I_{{\mathrm {2}}}f_{{\mathrm {2}}}+ I_{{\mathrm {3}}}f_{{\mathrm {3}}}+Ng\\N-Ng&=I_{{\mathrm {1}}}f_{{\mathrm {1}}}+I_ {{\mathrm {2}}}f_{{\mathrm {2}}}+I_{{\mathrm {3}}}f_{{\mathrm {3}}}}\\N(1-g)&= من }}f_{{\mathrm {3}}}\\N&=(I_{{\mathrm {1}}}f_{{\mathrm {1}}}+I_{{\mathrm {2}}}f_{ {\mathrm {2}}}+I_{{\mathrm {3}}}f_{{\mathrm {3}}})\div (1-g)\\N&=I_{{\mathrm {1}} }f_{{\mathrm {1}}}\div (1-g)+I_{{\mathrm {2}}}f_{{\mathrm {2}}}\div (1-g)+I_{{ \mathrm {3}}}f_{{\mathrm {3}}}\div (1-g)\\\end{تراز شده}}$

مشخصات وب

در این وبلاگ به ریاضیات و کاربردهای آن و تحقیقات در آنها پرداخته می شود. مطالب در این وبلاگ ترجمه سطحی و اولیه است و کامل نیست.در صورتی سوال یا نظری در زمینه ریاضیات دارید مطرح نمایید .در صورت امکان به آن می پردازم. من دوست دارم برای یافتن پاسخ به سوالات و حل پروژه های علمی با دیگران همکاری نمایم.در صورتی که شما هم بامن هم عقیده هستید با من تماس بگیرید.
09132003030

ریاضیات

آموزش ریاضی