5-مختصات تعمیم یافته

توسط علی رضا نقش نیلچی | پنجشنبه بیست و یکم اردیبهشت ۱۴۰۲ | 11:52

آونگ دوتایی [ ویرایش ]

مزایای مختصات تعمیم یافته با تجزیه و تحلیل یک آونگ دوتایی آشکار می شود . برای دو جرم m i ( i = 1, 2 ) ، اجازه دهید r i = ( x i , y i ) ، i = 1, 2 دو مسیر آنها را مشخص کند. این بردارها دو معادله قید را برآورده می کنند،

$f_{1}(x_{1},y_{1},x_{2},y_{2})=\mathbf {r} _{1}\cdot \mathbf {r} _{1}- L_{1}^{2}=0$

$f_{2}(x_{1},y_{1},x_{2},y_{2})=(\mathbf {r} _{2}-\mathbf {r} _{1}) \cdot (\mathbf {r} _{2}-\mathbf {r} _{1})-L_{2}^{2}=0.$

فرمول معادلات لاگرانژ برای این سیستم شش معادله در چهار مختصات دکارتی x i , y i ( i = 1, 2 ) و دو ضریب لاگرانژ λ i ( i = 1, 2 ) بدست می دهد که از دو معادله قید ناشی می شوند.

اکنون مختصات تعمیم یافته θ i ( i = 1, 2) را معرفی کنید که موقعیت زاویه ای هر جرم آونگ دوتایی را از جهت عمودی مشخص می کند. در این صورت داریم

$\mathbf{r}_1 = (L_1\sin\theta_1, -L_1\cos\theta_1), \quad \mathbf{r}_2 = (L_1\sin\theta_1, -L_1\cos\theta_1) + (L_2\sin \theta_2، -L_2\cos\theta_2).$

نیروی گرانشی که بر روی جرم ها وارد می شود به وسیله:

$\mathbf{F}_1=(0,-m_1 گرم)،\quad \mathbf{F}_2=(0,-m_2 گرم)$

که در آن g شتاب ناشی از گرانش است. بنابراین، کار مجازی گرانش روی دو جرم در حالی که مسیرهای r i را دنبال می کنند ( i = 1, 2) با

$\delta W = \mathbf{F}_1\cdot\delta \mathbf{r}_1 + \mathbf{F}_2\cdot\delta \mathbf{r}_2.$

تغییرات δ r i ( i = 1، 2) را می توان محاسبه کرد

$\delta \mathbf{r}_1 = (L_1\cos\theta_1, L_1\sin\theta_1)\delta\theta_1, \quad \delta \mathbf{r}_2 = (L_1\cos\theta_1, L_1\sin\theta_1 )\delta\theta_1 +(L_2\cos\theta_2, L_2\sin\theta_2)\delta\theta_2$

بنابراین، کار مجازی توسط داده شده است

$\delta W = -(m_1+m_2)gL_1\sin\theta_1\delta\theta_1 - m_2gL_2\sin\theta_2\delta\theta_2،$

و نیروهای تعمیم یافته هستند

$F_{\theta_1} = -(m_1+m_2)gL_1\sin\theta_1،\quad F_{\theta_2} = -m_2gL_2\sin\theta_2.$

انرژی جنبشی این سیستم را محاسبه کنید

$T= \frac{1}{2}m_1 \mathbf{v}_1\cdot\mathbf{v}_1 + \frac{1}{2}m_2 \mathbf{v}_2\cdot\mathbf{v}_2 = \frac{1}{2}(m_1+m_2)L_1^2\dot{\theta}_1^2 + \frac{1}{2}m_2L_2^2\dot{\theta}_2^2 + m_2L_1L_2 \cos (\theta_2-\theta_1)\dot{\theta}_1\dot{\theta}_2.$

معادله اویلر-لاگرانژ دو معادله در مختصات تعمیم یافته ناشناخته θ i ( i = 1, 2) ارائه شده توسط [14] به دست می دهد.

$(m_{1}+m_{2})L_{1}^{2}{\ddot {\theta }}_{1}+m_{2}L_{1}L_{2}{\ddot {\theta }}_{2}\cos(\theta _{2}-\theta _{1})+m_{2}L_{1}L_{2}{\dot {\theta _{2}} }^{2}\sin(\theta _{1}-\theta _{2})=-(m_{1}+m_{2})gL_{1}\sin \theta _{1}،$

$m_{2}L_{2}^{2}{\ddot {\theta }}_{2}+m_{2}L_{1}L_{2}{\ddot {\theta }}_{ 1}\cos(\theta _{2}-\theta _{1})+m_{2}L_{1}L_{2}{\dot {\theta _{1}}}^{2}\sin (\theta _{2}-\theta _{1})=-m_{2}gL_{2}\sin \theta _{2}.$

استفاده از مختصات تعمیم یافته θ i ( i = 1، 2) جایگزینی برای فرمول دکارتی دینامیک آونگ دوتایی فراهم می کند.

آونگ کروی [ ویرایش ]

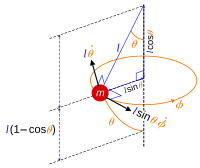
آونگ کروی: زوایا و سرعت ها.

برای مثال سه بعدی، یک آونگ کروی با طول ثابت l آزاد برای نوسان در هر جهت زاویه‌ای تحت تأثیر گرانش، محدودیت در باب آونگ را می‌توان به شکل بیان کرد.

$f(\mathbf {r} )=x^{2}+y^{2}+z^{2}-l^{2}=0\,,$

جایی که می توان موقعیت باب آونگ را نوشت

$\mathbf {r} =(x(\theta,\phi),y(\theta,\phi),z(\theta,\phi))\,,$

که در آن ( θ , φ ) زوایای قطبی کروی هستند زیرا باب در سطح یک کره حرکت می کند. موقعیت r در امتداد نقطه تعلیق تا باب اندازه گیری می شود که در اینجا به عنوان یک ذره نقطه در نظر گرفته می شود . یک انتخاب منطقی از مختصات تعمیم یافته برای توصیف حرکت زوایای ( θ , φ ) هستند . فقط دو مختصات به جای سه مورد نیاز است، زیرا موقعیت باب را می توان با دو عدد پارامتر کرد و معادله محدودیت سه مختصات ( x ، y ، z ) را به هم متصل می کند.بنابراین هر یک از آنها از دو دیگر مشخص می شود.

مختصات تعمیم یافته و کار مجازی [ ویرایش ]

اصل کار مجازی بیان می کند که اگر یک سیستم در تعادل ایستا باشد، کار مجازی نیروهای اعمال شده برای تمام حرکات مجازی سیستم از این حالت صفر است، یعنی δ W = 0 برای هر تغییر δ r . [15] هنگامی که بر حسب مختصات تعمیم یافته فرمول بندی می شود، معادل این شرط است که نیروهای تعمیم یافته برای هر جابجایی مجازی صفر باشد، یعنی F i = 0 .

بگذارید نیروهای وارد بر سیستم F j باشد ( j = 1, 2, …, m ) به نقاطی با مختصات دکارتی rj ( j = 1, 2, …, m ) اعمال شود ، سپس کار مجازی توسط یک جابجایی مجازی ایجاد می شود . از موقعیت تعادل توسط داده می شود

$\delta W = \sum_{j=1}^m \mathbf{F}_j\cdot \delta\mathbf{r}_j.$

جایی که δ r j ( j = 1, 2, …, m ) نشان دهنده جابجایی های مجازی هر نقطه از بدن است.

حال فرض کنید که هر δ r j به مختصات تعمیم یافته q i بستگی دارد ( i = 1, 2, …, n ) سپس

$\delta \mathbf{r}_j = \frac{\partial \mathbf{r}_j}{\partial q_1} \delta{q}_1 + \ldots + \frac{\partial \mathbf{r}_j}{\ جزئی q_n} \delta{q}_n،$

$\delta W = \left(\sum_{j=1}^m \mathbf{F}_j\cdot \frac{\partial \mathbf{r}_j}{\partial q_1}\right) \delta{q}_1 + \ldots + \left(\sum_{j=1}^m \mathbf{F}_j\cdot \frac{\partial \mathbf{r}_j}{\partial q_n}\right) \delta{q}_n .$

n شرایط _

$F_i = \sum_{j=1}^m \mathbf{F}_j\cdot \frac{\partial \mathbf{r}_j}{\partial q_i},\quad i=1,\ldots, n,$

نیروهای تعمیم یافته ای هستند که بر روی سیستم عمل می کنند. کین [16] نشان می دهد که این نیروهای تعمیم یافته را می توان بر حسب نسبت مشتقات زمانی نیز فرموله کرد.

$F_i = \sum_{j=1}^m \mathbf{F}_j\cdot \frac{\partial \mathbf{v}_j}{\partial \dot{q}_i},\quad i=1,\ldots ، n ،$

که در آن v j سرعت نقطه اعمال نیروی F j است .

برای اینکه کار مجازی برای یک جابجایی مجازی دلخواه صفر شود، هر یک از نیروهای تعمیم یافته باید صفر باشد، یعنی

$\delta W = 0 \quad \Rightarrow \quad F_i =0, i=1,\ldots, n.$

همچنین ببینید [ ویرایش ]

ویکی‌نقل نقل قول‌هایی مربوط به مختصات تعمیم‌یافته دارد .

یادداشت ها [ ویرایش ]

^ برخی از نویسندگان به عنوان مثال Hand & Finch شکل بردار موقعیت برای ذره k را می گیرند ، همانطور که در اینجا نشان داده شده است، به عنوان شرط برای هولونومیک بودن محدودیت در آن ذره.

^ برخی از نویسندگان معادلات محدودیت را برای راحتی با برخی از معادلات محدودیت (مثلاً آونگ ها) روی یک ثابت قرار می دهند، برخی دیگر آن را صفر می کنند. فرقی نمی کند زیرا ثابت را می توان کم کرد تا در یک طرف معادله صفر شود. همچنین در معادلات لاگرانژ از نوع اول فقط مشتقات مورد نیاز است.

منابع

https://en.wikipedia.org/wiki/Generalized_coordinates

مشخصات وب

در این وبلاگ به ریاضیات و کاربردهای آن و تحقیقات در آنها پرداخته می شود. مطالب در این وبلاگ ترجمه سطحی و اولیه است و کامل نیست.در صورتی سوال یا نظری در زمینه ریاضیات دارید مطرح نمایید .در صورت امکان به آن می پردازم. من دوست دارم برای یافتن پاسخ به سوالات و حل پروژه های علمی با دیگران همکاری نمایم.در صورتی که شما هم بامن هم عقیده هستید با من تماس بگیرید.
09132003030

ریاضیات

آموزش ریاضی