1-مختصات تعمیم یافته

توسط علی رضا نقش نیلچی | پنجشنبه بیست و یکم اردیبهشت ۱۴۰۲ | 11:39

از ویکیپدیا، دانشنامه آزاد

مکانیک کلاسیک
بخشی از یک سریال در
${\textbf {F}}={\frac {d}{dt}}(m{\textbf {v}})$ قانون دوم حرکت
تاریخ جدول زمانی کتاب های درسی
نشان می دهد شاخه ها
نشان می دهد مبانی
پنهان شدن فرمولاسیون قوانین حرکت نیوتن مکانیک تحلیلی مکانیک لاگرانژی مکانیک هامیلتونی مکانیک روتین معادله همیلتون-جاکوبی معادله حرکت اپل مکانیک کوپمن-فون نیومن
نشان می دهد موضوعات اصلی
نشان می دهد چرخش
نشان می دهد دانشمندان
پورتال فیزیک دسته بندی
v تی ه

در مکانیک تحلیلی مختصات تعمیم یافته مجموعه ای از پارامترها هستند که برای نمایش وضعیت یک سیستم در یک فضای پیکربندی استفاده می شوند . این پارامترها باید پیکربندی سیستم را نسبت به یک حالت مرجع به طور منحصر به فرد تعریف کنند. [1] سرعت های تعمیم یافته مشتقات زمانی مختصات تعمیم یافته سیستم هستند. صفت "تعمیم یافته" این پارامترها را از استفاده سنتی اصطلاح "مختصات" برای اشاره به مختصات دکارتی متمایز می کند .

مثالی از مختصات تعمیم یافته، توصیف موقعیت یک آونگ با استفاده از زاویه آونگ نسبت به عمودی است، نه با موقعیت x و y آونگ.

اگرچه ممکن است گزینه‌های زیادی برای مختصات تعمیم‌یافته برای یک سیستم فیزیکی وجود داشته باشد، اما معمولاً برای ساده کردن محاسبات، مانند حل معادلات حرکت برای سیستم، انتخاب می‌شوند. اگر مختصات مستقل از یکدیگر باشند، تعداد مختصات تعمیم یافته مستقل با تعداد درجات آزادی سیستم تعریف می شود. [2] [3]

مختصات تعمیم یافته با گشتاور تعمیم یافته جفت می شوند تا مختصات متعارفی را در فضای فاز ارائه کنند .

محدودیت ها و درجات آزادی [ ویرایش ]

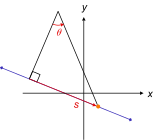
راه مستقیم را باز کنید

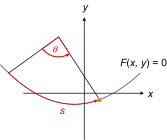
مسیر منحنی F ( x , y ) = 0 را باز کنید

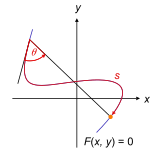
مسیر منحنی بسته C ( x , y ) = 0

یک مختصات تعمیم یافته (یک درجه آزادی) در مسیرهای دو بعدی. فقط یک مختصات تعمیم یافته برای مشخص کردن موقعیت های منحصر به فرد روی منحنی مورد نیاز است. در این مثال ها، آن متغیر یا طول قوس s یا زاویه θ است . داشتن هر دو مختصات دکارتی ( x , y ) غیر ضروری است زیرا x یا y با معادلات منحنی ها به دیگری مربوط می شود. آنها همچنین می توانند با s یا θ پارامتر شوند .

باز کردن مسیر منحنی F ( x , y ) = 0 . تقاطع های متعدد شعاع با مسیر.

مسیر منحنی بسته C ( x , y ) = 0 . خود تقاطع مسیر.

طول قوس s در امتداد منحنی یک مختصات تعمیم یافته قانونی است زیرا موقعیت به طور منحصر به فرد تعیین می شود، اما زاویه θ اینگونه نیست زیرا موقعیت های متعددی برای یک مقدار θ وجود دارد .

مختصات تعمیم یافته معمولاً برای ارائه حداقل تعداد مختصات مستقلی که پیکربندی یک سیستم را تعریف می کند، انتخاب می شوند، که فرمول بندی معادلات حرکت لاگرانژ را ساده می کند. با این حال، ممکن است مجموعه مفیدی از مختصات تعمیم یافته نیز وابسته باشند ، به این معنی که آنها با یک یا چند معادله محدودیت مرتبط هستند.

محدودیت های هولونومیک [ ویرایش ]

سطح منحنی باز F ( x ، y ، z ) = 0

سطح منحنی بسته S ( x ، y ، z ) = 0

دو مختصات تعمیم یافته، دو درجه آزادی، روی سطوح منحنی به صورت سه بعدی. فقط دو عدد ( u , v ) برای تعیین نقاط روی منحنی مورد نیاز است، یک امکان برای هر مورد نشان داده شده است. سه مختصات دکارتی کامل ( x ، y ، z ) ضروری نیستند زیرا هر دو، سومی را با توجه به معادلات منحنی ها تعیین می کنند.

برای سیستمی از ذرات N در فضای مختصات واقعی سه بعدی ، بردار موقعیت هر ذره را می توان به صورت سه تایی در مختصات دکارتی نوشت :

${\begin{aligned}&\mathbf {r} _{1}=(x_{1},y_{1},z_{1}),\\&\mathbf {r} _{2}= (x_{2}،y_{2}،z_{2})،\\&\qquad \qquad \vdots \\&\mathbf {r} _{N}=(x_{N}،y_{N}، z_{N})\end{تراز شده}}$

هر یک از بردارهای موقعیت را می توان r k نشان داد که در آن k = 1، 2، ...، N ذرات را برچسب گذاری می کند. یک محدودیت هولونومیک معادله قیدی شکل ذره k است [4] [a]

$f(\mathbf{r}_k، t) = 0$

که هر 3 مختصات فضایی آن ذره را به هم متصل می کند، بنابراین مستقل نیستند. محدودیت ممکن است با زمان تغییر کند، بنابراین زمان t به صراحت در معادلات محدودیت ظاهر می شود. در هر لحظه از زمان، هر مختصاتی از مختصات دیگر تعیین می شود، به عنوان مثال اگر x k و z k داده شوند، y k نیز چنین است . یک معادله محدودیت به عنوان یک قید محسوب می شود. اگر قیود C وجود داشته باشد ، هر کدام یک معادله دارند، بنابراین C وجود خواهد داشتمعادلات محدودیت لزوماً یک معادله محدودیت برای هر ذره وجود ندارد، و اگر هیچ محدودیتی در سیستم وجود نداشته باشد، هیچ معادله محدودیتی وجود ندارد.

تا کنون، پیکربندی سیستم با 3 N کمیت تعریف شده است، اما مختصات C را می توان حذف کرد، یک مختصات از هر معادله محدودیت. تعداد مختصات مستقل n = 3 N - C است . (در ابعاد D ، پیکربندی اصلی به مختصات ND نیاز دارد و کاهش توسط محدودیت ها به معنای n = ND - C است ). ایده آل است که از حداقل تعداد مختصات مورد نیاز برای تعریف پیکربندی کل سیستم استفاده کنید، در حالی که از محدودیت های موجود در سیستم استفاده کنید. این کمیت ها به عنوان مختصات تعمیم یافته شناخته می شونددر این زمینه، q j ( t ) نشان داده شده است . جمع آوری آنها در یک n - تاپل راحت است

$\mathbf {q} (t)=(q_{1}(t),\ q_{2}(t),\ \ldots ,\ q_{n}(t))$

که نقطه ای در فضای پیکربندی سیستم است. همه آنها مستقل از یکدیگر هستند و هر کدام تابع زمان هستند. از نظر هندسی آنها می توانند طول در امتداد خطوط مستقیم، یا طول قوس در امتداد منحنی ها، یا زاویه باشند. نه لزوما مختصات دکارتی یا سایر مختصات متعامد استاندارد . برای هر درجه آزادی یکی وجود دارد ، بنابراین تعداد مختصات تعمیم یافته برابر است با تعداد درجات آزادی، n . درجه آزادی مربوط به کمیتی است که پیکربندی سیستم را تغییر می‌دهد، برای مثال زاویه یک آونگ، یا طول قوسی که توسط یک مهره در امتداد یک سیم عبور می‌کند.

اگر بتوان از روی قیود به تعداد درجات آزادی متغیر مستقل را پیدا کرد، می توان از آنها به عنوان مختصات تعمیم یافته استفاده کرد. [5] بردار موقعیت r k ذره k تابعی از تمام n مختصات تعمیم یافته (و از طریق آنها، زمان) است، [6] [7] [8] [5] [nb 1]

$\mathbf {r} _{k}=\mathbf {r} _{k}(\mathbf {q} (t))\,,$

و مختصات تعمیم یافته را می توان به عنوان پارامترهای مرتبط با محدودیت در نظر گرفت.

مشتقات زمانی مربوط به q سرعت های تعمیم یافته هستند،

${\dot {\mathbf {q} }}={\frac {d\mathbf {q} }{dt}}=({\dot {q}}_{1}(t),\ {\ نقطه {q}}_{2}(t)،\ \ldots،\ {\dot {q}}_{n}(t))$

(هر نقطه روی یک مقدار نشان دهنده یک مشتق زمانی است ). بردار سرعت v k مشتق کل r k نسبت به زمان است

$\mathbf {v} _{k}={\dot {\mathbf {r} }}_{k}={\frac {d\mathbf {r} _{k}}{dt}}=\ مجموع _{j=1}^{n}{\frac {\partial \mathbf {r} _{k}}{\partial q_{j}}}{\dot {q}}_{j}\,.$

و بنابراین به طور کلی به سرعت ها و مختصات تعمیم یافته بستگی دارد. از آنجایی که می‌توانیم مقادیر اولیه مختصات و سرعت‌های تعمیم‌یافته را جداگانه مشخص کنیم، مختصات تعمیم‌یافته qj و سرعت‌های dq j / dt را می‌توان به عنوان متغیرهای مستقل در نظر گرفت .

محدودیت‌های غیرهولونومیک [ ویرایش ]

یک سیستم مکانیکی می تواند شامل محدودیت هایی در مختصات تعمیم یافته و مشتقات آنها باشد. محدودیت هایی از این نوع به عنوان غیرهولونومیک شناخته می شوند. محدودیت‌های غیرهولونومیک مرتبه اول این شکل را دارند

$g(\mathbf{q}, \dot{\mathbf{q}}, t) = 0\,,$

نمونه ای از چنین محدودیتی چرخ غلتشی یا لبه چاقویی است که جهت بردار سرعت را محدود می کند. محدودیت‌های غیرهولونومیک همچنین می‌توانند مشتقات مرتبه بعدی مانند شتاب‌های تعمیم‌یافته را شامل شوند.

مشخصات وب

در این وبلاگ به ریاضیات و کاربردهای آن و تحقیقات در آنها پرداخته می شود. مطالب در این وبلاگ ترجمه سطحی و اولیه است و کامل نیست.در صورتی سوال یا نظری در زمینه ریاضیات دارید مطرح نمایید .در صورت امکان به آن می پردازم. من دوست دارم برای یافتن پاسخ به سوالات و حل پروژه های علمی با دیگران همکاری نمایم.در صورتی که شما هم بامن هم عقیده هستید با من تماس بگیرید.
09132003030

ریاضیات

آموزش ریاضی