ریاضیات

کاربرد قانون گاوس

کاربردهای مختلفی از قانون گاوس وجود دارد که اکنون به آنها خواهیم پرداخت. فقط برای شروع، می دانیم که مواردی وجود دارد که در آنها محاسبه میدان الکتریکی بسیار پیچیده است و شامل یکپارچگی سخت است . ما از قانون گاوس برای ساده کردن ارزیابی میدان الکتریکی به روشی آسان استفاده می کنیم.

قبل از اینکه درباره برنامه ها بیشتر بیاموزیم، ابتدا ببینیم چگونه می توانیم قانون را اعمال کنیم . ما باید یک سطح گاوسی را انتخاب کنیم، به طوری که ارزیابی میدان الکتریکی آسان شود. برای آسان کردن مسائل باید از تقارن استفاده کرد. همچنین باید به یاد داشته باشیم که لزومی ندارد که سطح گاوسی با سطح واقعی منطبق باشد. این می تواند در داخل یا خارج از سطح گاوسی باشد.

میدان الکتریکی به دلیل سیم بی نهایت

اجازه دهید یک سیم بی نهایت طولانی با چگالی بار خطی λ و طول L را در نظر بگیریم. برای محاسبه میدان الکتریکی، سطح گاوسی استوانه ای را در نظر می گیریم. از آنجایی که میدان الکتریکی E در جهت شعاعی است، شار از انتهای سطح استوانه ای صفر خواهد بود.

دلیل آن این است که میدان الکتریکی و بردار مساحت بر یکدیگر عمود هستند. از آنجایی که میدان الکتریکی بر هر نقطه از سطح منحنی عمود است، می توان گفت که قدر آن ثابت خواهد بود.

مساحت سطح استوانه ای منحنی 2πrl است. شار الکتریکی از طریق منحنی است

E × 2πrl

طبق قانون گاوس

باید به خاطر داشته باشید که اگر چگالی بار خطی مثبت باشد، جهت میدان الکتریکی به صورت شعاعی به سمت بیرون است. از سوی دیگر، اگر چگالی بار خطی منفی باشد، شعاعی به سمت داخل خواهد بود.

میدان الکتریکی به دلیل ورق صفحه بی نهایت

اجازه دهید یک صفحه صفحه بی نهایت، با چگالی بار سطحی σ و سطح مقطع A را در نظر بگیریم. موقعیت صفحه صفحه بی نهایت به صورت زیر است:

جهت میدان الکتریکی ناشی از یک ورقه بار بی نهایت عمود بر صفحه ورق است. اجازه دهید یک سطح گاوسی استوانه ای را در نظر بگیریم که محور آن نسبت به صفحه ورق عموداست. می‌توان میدان الکتریکی E را از قانون گاوس مطابق قانون ارزیابی کرد:

از یک بار توزیع بار پیوسته q چگالی بار (σ) برابر مساحت (A) خواهد بود. در مورد شار خالص الکتریکی صحبت می کنیم، شار الکتریکی را فقط از دو سر سطح گاوسی فرضی در نظر خواهیم گرفت. می‌توانیم آن را به این واقعیت نسبت دهیم که سطح منحنی و میدان الکتریکی نسبت به یکدیگر نرمال هستند و در نتیجه شار الکتریکی صفر تولید می‌کنند. بنابراین شار الکتریکی خالص است

Φ = EA – (– EA)

Φ = 2EA

سپس، می توانیم بنویسیم

عبارت A cancels out به معنای میدان الکتریکی ناشی از صفحه صفحه بی نهایت مستقل از سطح مقطع A است و برابر است با:

میدان الکتریکی به دلیل پوسته کروی نازک

اجازه دهید یک پوسته کروی نازک با چگالی بار سطحی σ و شعاع "R" را در نظر بگیریم. با مشاهده می توان دریافت که پوسته دارای تقارن کروی است. بنابراین، می‌توان میدان الکتریکی ناشی از پوسته کروی را در دو موقعیت مختلف ارزیابی کرد:

• میدان الکتریکی خارج از پوسته کروی
• میدان الکتریکی در داخل پوسته کروی

اجازه دهید این دو مورد را با جزئیات بیشتری بررسی کنیم.

میدان الکتریکی خارج از پوسته کروی

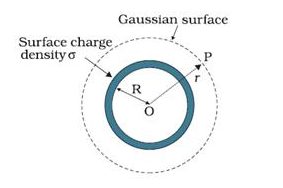
برای یافتن میدان الکتریکی خارج از پوسته کروی، نقطه P را در خارج از پوسته در فاصله r از مرکز پوسته کروی می گیریم. با تقارن، سطح کروی گاوسی را با شعاع r و مرکز O در نظر می گیریم. سطح گاوسی از P عبور می کند و میدان الکتریکی ثابت  E  را در اطراف تجربه می کند زیرا همه نقاط به طور مساوی "r" از مرکز کره فاصله دارند . سپس طبق قانون گاوس:

بار محصور شده در داخل سطح گاوسی q σ × 4 πR ^2 خواهد بود. کل شار الکتریکی از طریق سطح گاوسی خواهد بود

Φ = E × 4 πr ^2

سپس با قانون گاوس، می توانیم بنویسیم

با قرار دادن مقدار چگالی بار سطحی σ به عنوان q/4 πR ^2 ، می توانیم میدان الکتریکی را به صورت بازنویسی کنیم.

در شکل برداری، میدان الکتریکی است

که r بردار شعاع است که جهت میدان الکتریکی را نشان می دهد . آنچه در اینجا باید به آن توجه کنیم این است که اگر چگالی بار سطحی σ منفی باشد، جهت میدان الکتریکی به صورت شعاعی به سمت داخل خواهد بود.

میدان الکتریکی در داخل پوسته کروی

برای ارزیابی میدان الکتریکی داخل پوسته کروی، یک نقطه P را در داخل پوسته کروی در نظر می گیریم. با تقارن، دوباره یک سطح گاوسی کروی را می گیریم که از P می گذرد، در مرکز O و با شعاع r. حالا طبق قانون گاوس

شار الکتریکی خالص E × 4 π r^ 2 خواهد بود.

مثال حل شده برای شما

سوال: چرا میدان الکتریکی درون پوسته کروی وجود ندارد؟

راه حل: بار محصور q صفر خواهد بود، زیرا می دانیم که چگالی بار سطحی در خارج از سطح پراکنده است، بنابراین هیچ باری در داخل پوسته کروی وجود ندارد. بنابراین، E = 0

این بحث ما را در مورد موضوع کاربرد قانون گاوس به پایان می رساند.

منبع

https://www.toppr.com/guides/physics/electric-charges-and-fields/applications-of-gauss-law/