ریاضیات

گروه های متناهی تا مرتبه9

برای فهرست بندی تمام گروه های متناهی بامرتبه9 ، از نتایج زیر استفاده می کنیم:

قضیه . یک گروه متناهی از مرتبه اعداد اول دوری است.

در نتیجه تنها یک گروه از هر یک از مرتبه های وجود دارد ، یعنی گروه های چرخهای ، ، و .

گروه های مرتبه 4 و 9 شامل قضیه می شوند:

قضیه . اجازه دهید که منظور از یک گروه است ، که در آن یک عدد اول است. سپس آبلی است. علاوه بر این ، یا مرتب دوری است ، یا ضرب مستقیم دو گروه دوری از مرتبه است .

این نتیجه نشان می دهد که دو گروه از مرتبه 4 و 9 وجود دارد. این گروه ها گروه های حلقوی یا ، یا ، و هستند . هر کدام از آنها آبلی هستند.

این گروه به عنوان گروه کلاین چهار نیز شناخته می شود  .

اجازه دهید یک گروه از مرتبه 8. قضیه لاگرانژ نشان می دهد که مرتبه عنصر تقسیم می کند مرتبه ، یعنی 8. بنابراین هر عنصر دارای مرتبه 1،2،4 یا 8 است.

اگر عنصری از مرتبه 8 وجود داشته باشد ، دوری است ، یعنی .

اگر هیچ عنصر مرتبه 4 را شامل نمی شود ، باید از عناصر با مرتبه 2 (و همانی) تشکیل شود. به راحتی می توان دریافت که چنین گروهی آبلی هستند. یعنی ، در این مورد ، یعنی برای هر . سپس برای هر .

بنابراین ، برای غیرآبلی بودن ، باید یک عنصر مرتبه 4 داشته باشد. این به ما می دهد 4 عناصر : . اگر عنصری متفاوت از یکی از این موارد با مرتبه 2 وجود دارد ، به عنوان مثال ، از آنجا که مرتبه 4 نیز دارد و گروه ایجاد شده توسط آن یک زیر گروه نرمال است (زیرا فقط 2 کاست). این دلالت می کنه که:

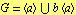• تجزیه ستون سمت چپ از 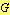و است 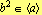. این به آن 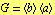و آن دلالت دارد .
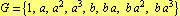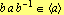• به از آنجا که 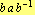از درجه 4 ، 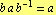یا 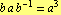. مورد اول دلالت بر آن دارد 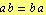، و آن 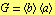یا آن 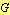آبلی ، یک تناقض است.  

در نتیجه . از آنجا که و از برابری و غیر ممکن است. در هر دو مورد ، و از آن زمان ، آبلی خواهد بود. بنابراین باقی می ماند که و و گروه حاصله گروه دی هدرال است .

این گروه توسط دو عنصر ایجاد می شود و ، جایی که از مرتبه 4 ، از مرتبه 2 است ، به گونه ای که .

بنابراین این امر باعث می شود که همه عناصر عدم وابستگی باید دارای مرتبه 4 باشند. یکی از این موارد باشد. از آنجا که مرتبه 2 دارد ، باید برابر باشد. عنصر نمی تواند قدرت یا . بنابراین دوباره مرتبه 4. عناصر هستند بنابراین . این گروه نسبت به گروه کواترنیون یکریخت است  .

این گروه توسط دو عنصر ایجاد می شود و هر دو از مرتبه 4 به این مرتبه و . هنگام استفاده از واحدهای کواترنیون برای توصیف ، ایزومورفیسم با نگاشت به و به داده می شود .

برای گروه های درجه 6 ما دو احتمال داریم: گروه حلقوی یا ضرب مستقیم دو گروه حلقوی .