ادامه نوار موبیوس

توسط علی رضا نقش نیلچی | شنبه بیست و نهم خرداد ۱۴۰۰ | 11:39

هندسه و توپولوژی [ ویرایش ]

شیئی که در یک جهان به شکل نوار موبیوس وجود داشته باشد ، از تصویر آینه ای آن قابل تشخیص نیست - پنجه بزرگتر این خرچنگ کمانچه با هر گردش از چپ به راست تغییر می کند. غیرممکن است که جهان بتواند این خاصیت را داشته باشد. کرم چاله غیر جهت دار را ببینید

یکی از راه های نمایش نوار موبیوس تعبیه شده در فضای اقلیدسی سه بعدی با استفاده از پارامتر است:

${\ displaystyle {\ start {تراز شده} x (u ، v) & = \ چپ (1 + {\ frac {v} {2}} \ cos {\ frac {u} {2}} \ راست) \ cos u \\ y (u، v) & = \ left (1 + {\ frac {v} {2}} \ cos {\ frac {u} {2}} \ right) \ sin u \\ z (u، v ) & = {\ frac {v} {2}} \ sin {\ frac {u} {2}} \\\ end {تراز شده}}}$

برای ${\ displaystyle 0 \ leq u <2 \ pi}$ و ${\ displaystyle -1 \ leq v \ leq 1}$ . این یک نوار Möbius به عرض 1 ایجاد می کند که دایره مرکزی آن شعاع 1 دارد و در آن قرار دارد $xy$ و مرکز آن است $(0،0،0)$ . پارامتر u در اطراف نوار اجرا می شود در حالی که v از یک لبه به لبه دیگر منتقل می شود.

در مختصات قطبی استوانه ای $(r ، \ تتا ، z)$ ، یک نسخه محدود از نوار Möbius را می توان با معادله نشان داد:

${\ displaystyle \ log (r) \ sin \ left ({\ tfrac {1} {2}} \ theta \ right) = z \ cos \ left ({\ tfrac {1} {2}} \ theta \ right) .}$

گسترده ترین تعبیه ایزومتریک در 3 فضا [ ویرایش ]

اگر یک نوار صاف موبیوس در سه فضا یک مستطیل باشد - یعنی از شناسایی دو ضلع مخالف یک مستطیل هندسی با خم شدن اما کشیده نشدن سطح ایجاد شده است - در صورت وجود نسبت ابعاد ، چنین تعبیه ای ممکن است شناخته شود. مستطیل بزرگتر از است ${\ sqrt 3}$ ، با اضلاع کوتاه تر مشخص شده است. (برای نسبت ابعادی کوچکتر ، مشخص نیست که امکان تعبیه صاف وجود دارد.) با کاهش نسبت ابعاد به سمت ${\ sqrt 3}$ ، به نظر می رسد هر چنین تعبیه ای به شکلی نزدیک می شود که می توان آن را نواری از سه مثلث متساوی الاضلاع تصور کرد که روی هم جمع شده اند تا مثلث متساوی الاضلاع را اشغال کنند.

اگر نوار موبیوس در سه فضا فقط یک بار به طور مداوم قابل تغییر باشد (کلاس $C_ {1}$ ) ، با این وجود قضیه نش-کوایپر نشان می دهد که هیچ حد پایینی وجود ندارد.

یک روش ساخت نوار موبیوس از یک نوار مستطیلی بیش از حد گسترده برای چرخاندن ساده و اتصال (به عنوان مثال ، یک مستطیل فقط یک واحد طول و یک واحد عرض) این است که ابتدا جهت عریض را به عقب و جلو با استفاده از تعداد زوج تا بزنید - "برابر آکاردئون" - به طوری که نوار تا شده به اندازه کافی باریک شود که بتوان آن را پیچ و تاب کرد و بهم پیوست ، همان اندازه که یک نوار تنها به اندازه کافی طولانی می تواند به هم متصل شود. [10] با دو برابر ، به عنوان مثال ، a $1 \ بار 1$ نوار تبدیل خواهد شد ${\ displaystyle 1 \ times {\ tfrac {1} {3}}}$ نوار تا شده ای که سطح مقطع آن به شکل 'N' باشد و پس از نیم پیچ خوردن 'N' باقی بماند. این نوار تا شده ، سه برابر عرض آن ، به اندازه کافی بلند است که سپس در انتها به هم متصل شود. این روش در اصل کار می کند ، اما در صورت استفاده از کاغذ ، پس از تا خوردگی به اندازه کافی غیر عملی می شود. با استفاده از کاغذ معمولی ، می توان این ساختار را صاف و با تمام لایه های کاغذ در یک صفحه واحد تا کرد ، اما از نظر ریاضی ، آیا بدون کشش سطح مستطیل این امکان وجود ندارد. [11]

توپولوژی [ ویرایش ]

برای تبدیل مستطیل به نوار موبیوس ، لبه های دارای برچسب A را به هم متصل کنید تا جهت فلش ها مطابقت داشته باشد.

از نظر توپولوژی ، نوار موبیوس را می توان مربع تعریف کرد ${\ displaystyle [0،1] \ times [0،1]}$ با دو طرف بالا و پایین آن با رابطه مشخص می شود ${\ displaystyle (x ، 0) \ sim (1-x، 1)}$ برای $0 \ le x \ le 1$ ، همانطور که در نمودار نشان داده شده است.

ارائه کمتر استفاده شده از نوار موبیوس به عنوان ضریب توپولوژیکی یک توروس است. [12] یک توروس می تواند به عنوان مربع ساخته شود ${\ displaystyle [0،1] \ times [0،1]}$ با لبه های مشخص شده ${\ displaystyle (0، y) \ sim (1، y)}$ (چسب از چپ به راست) و ${\ displaystyle (x ، 0) \ sim (x، 1)}$ (چسب پایین به بالا). اگر یکی نیز شناسایی شود ${\ displaystyle (x، y) \ sim (y، x)}$ ، سپس نوار موبیوس بدست می آید. مورب مربع (نقاط ${\ displaystyle (x ، x)}$ جایی که هر دو مختصات اتفاق نظر دارند) به مرز نوار موبیوس تبدیل می شود ، و دارای یک ساختار دو شاخه است ، که از لحاظ هندسی با "بازتاب" مطابقت دارد - ژئودزیک ها (خطوط مستقیم) در نوار موبیوس از لبه به سمت نوار منعکس می شوند. از نظر نمایی ، اینطور نوشته شده است ${\ displaystyle T ^ {2} / S ^ {2}}$ - 2-چنبره quotiented توسط اقدام گروه از گروه متقارن در دو نامه (تعویض مختصات)، و می توان آن را به عنوان فکر فضای پیکربندی از دو نقطه نامرتب بر روی دایره، احتمالا همان (مربوط لبه به نقاط همان)) ، با تورس مربوط به دو نقطه مرتب بر روی دایره.

نوار موبیوس یک منیفولد فشرده دو بعدی (یعنی یک سطح ) با مرز است. این یک نمونه استاندارد از سطحی است که جهت پذیر نیست . در حقیقت ، نوار موبیوس نمونه ای از پدیده توپولوژیکی عدم جهت گیری است . دلیل این امر آنست که اشکال دو بعدی (سطوح) کمترین ابعادی هستند که غیر قابل جهت گیری برای آنها امکان پذیر است و نوار موبیوس تنها سطحی است که از نظر توپولوژیکی یک فضای فرعی از هر سطح غیرقابل جهت است. در نتیجه ، هر سطحی غیر قابل منشأ است اگر و فقط در صورت وجود یک باند Möbius به عنوان یک فضایی فرعی باشد.

نوار Möbius نیز یک نمونه استاندارد است که برای نشان دادن مفهوم ریاضی بسته نرم افزاری فیبر استفاده می شود . به طور خاص ، این یک بسته غیرمستقیم بر روی دایره است $S ^ {1}$ با فیبر آن برابر با فاصله واحد ، $من = [0،1]$ . نگاه کردن فقط به لبه نوار موبیوس دو امتیاز غیرمنتظره (یا $\ mathbb {Z} _ {2}$ ) بسته بیش از $S ^ {1}$ .

گرافیک رایانه ای [ ویرایش ]

یک ساخت ساده از نوار Möbius که می تواند برای به تصویر کشیدن آن در گرافیک رایانه یا بسته های مدل سازی استفاده شود:

یک نوار مستطیلی بردارید. آن را حول یک نقطه ثابت بچرخانید نه در صفحه آن. در هر مرحله ، نوار را در امتداد یک خط در صفحه آن بچرخانید (خطی که نوار را به دو قسمت تقسیم می کند) و عمود بر شعاع اصلی مداری است. سطح تولید شده در یک دور کامل نوار موبیوس است.
یک نوار موبیوس بردارید و آن را در امتداد وسط نوار ببرید. این یک نوار جدید است ، که یک مستطیل است که با چرخاندن یک انتهای یک چرخش کامل به هم متصل می شود. با برش دوباره از وسط ، این دو نوار چرخشی بهم پیوسته را ایجاد می کند.

هندسه باند باز Möbius [ ویرایش ]

گروه Möbius باز است با حذف تشکیل مرزی از گروه استاندارد موبیوس. از مجموعه ساخته شده است ${\ displaystyle S = \ {(x، y) \ in \ mathbb {R} ^ {2} \ mid 0 \ leq x \ leq 1،0 <y <1 \}}$ با شناسایی (چسباندن) نقاط $(0 ، سال)$ و ${\ displaystyle (1،1-y)}$ برای همه ${\ displaystyle 0 <y <1}$ .

ممکن است به عنوان سطح انحنای ثابت ، منفی یا صفر (گوسی) ساخته شود . در موارد انحنای منفی و صفر ، باند Möbius می تواند به عنوان یک سطح کامل (از نظر ژئودزیکی) ساخته شود ، به این معنی که همه ژئودزیک ها ("خطوط مستقیم" روی سطح) ممکن است به طور نامحدود در هر دو جهت تمدید شوند.

انحنای منفی ثابت: [ ویرایش ]

مانند صفحه و استوانه باز ، باند باز Möbius نه تنها یک معیار کامل انحنای ثابت 0 ، بلکه یک متریک کامل از انحنای منفی ثابت را نیز پذیرفته است. یکی از راه های برای دیدن این است که با آغاز مدل هواپیما نیم بالا (پوانکاره) از هواپیما اغراقی ، هندسه انحناء ثابت که خطوط در مدل های نیم دایره که با نشان $ایکس$ محورها در زاویه های راست. زیر مجموعه نیمه صفحه بالایی را بین دو نیم دایره تو در تو قرار داده و نیم دایره بیرونی را با چرخش چپ و راست نیم دایره داخلی مشخص کنید. نتیجه از نظر توپولوژی یک باند کامل و غیر جمع و جور Möbius با انحنای منفی ثابت است.

انحنای صفر (ثابت): [ ویرایش ]

با شروع بخشي از صفحه نيز ممكن است اين سطح به عنوان يك سطح كامل ساخته شود $\ R ^ 2$ تعریف شده بوسیله ی ${\ displaystyle 0 \ leq y \ leq 1}$ و شناسایی $(x ، 0)$ با ${\ displaystyle (-x، 1)}$ برای همه ${\ displaystyle x \ in \ mathbb {R}}$ . متریک حاصل ، باند باز Möbius را به یک سطح مسطح (از نظر جغرافیایی) کامل تبدیل می کند (یعنی دارای انحنای گاوسی در همه جا برابر 0). این تنها معیار موجود در باند Möbius تا مقیاس بندی یکنواخت است که هم مسطح و هم کامل است.

انحنای مثبت ثابت: [ ویرایش ]

یک گروه موبیوس از انحنای ثابت ثابت نمی تواند کامل باشد ، زیرا شناخته شده است که تنها سطوح کامل انحنای مثبت ثابت کره و صفحه نمایش است . هواپیمای فرافکنی $\ mathbb {P} ^ {2}$ از انحنای ثابت 1+ ممکن است به عنوان ضریب کره واحد ساخته شود $S ^ {2}$ که در $\ mathbb {R} ^ {3}$ توسط نقشه antipodal ${\ displaystyle A: S ^ {2} \ به S ^ {2}}$ تعریف شده بوسیله ی ${\ displaystyle A (x، y، z) = (- x، -y، -z)}$ . باند موبیوس باز با صفحه نمایشی که یک بار سوراخ شده است هومومورفیک است ، یعنی $\ mathbb {P} ^ {2}$ با حذف یک نقطه این ممکن است نزدیکترین باری باشد که یک باند ثابت انحنای مثبت Möbius می تواند به یک سطح کامل برسد: فقط با یک نقطه فاصله.

فضای خطوط unoriented در هواپیما diffeomorphic به گروه Möbius باز است. [13] برای دیدن دلیل ، اجازه دهید ${\ displaystyle L (\ theta)}$ خط را از طریق مبدا در یک زاویه مشخص می کنیم $\ تتا$ به مثبت $ایکس$ -محور. برای هر ${\ displaystyle L (\ theta)}$ خانواده وجود دارد $P (\ تتا)$ از تمام خطوط موجود در صفحه عمود بر ${\ displaystyle L (\ theta)}$ . از نظر توپولوژی ، خانواده $P (\ تتا)$ فقط یک خط است (زیرا هر خط در $P (\ تتا)$ خط را قطع می کند ${\ displaystyle L (\ theta)}$ فقط در یک نقطه) به این ترتیب ، همانطور که $\ تتا$ در محدوده افزایش می یابد ${\ displaystyle 0 \ leq \ theta <\ pi}$ ، خط ${\ displaystyle L (\ theta)}$ خطوط متمایز یک خط را نشان می دهد. اما کی $\ تتا$ می رسد $\ پی$ ، ${\ displaystyle L (\ pi)}$ یکسان است با $L (0)$ ، و بنابراین خانواده ها $P (0)$ و ${\ displaystyle P (\ pi)}$ از خطوط عمود نیز خانواده های یکسانی هستند. خط $L (0)$ ، با این حال ، به عنوان خود بازگشت ${\ displaystyle L (\ pi)}$ در جهت مخالف اشاره کرد . هر خط در هواپیما دقیقاً با یک خط در برخی خانواده ها مطابقت دارد $P (\ تتا)$ ، دقیقاً برای یکی $\ تتا$ ، برای ${\ displaystyle 0 \ leq \ theta <\ pi}$ ، و ${\ displaystyle P (\ pi)}$ یکسان است با $P (0)$ اما برمی گردد در جهت مخالف. این اطمینان می دهد که فضای تمام خطوط در صفحه - اتحاد همه $P (\ تتا)$ برای ${\ displaystyle 0 \ leq \ theta <\ pi}$ - یک گروه باز Möbius است.

گروه تحولات خطی ذهنی ${\ displaystyle GL (2 ، \ mathbb {R})}$ هواپیما به خودش (واقعی $2 بار 2$ ماتریس هایی با تعیین کننده غیر صفر) به طور طبیعی باعث ایجاد اختلاف در فضای خطوط هواپیما به سمت خود می شود که گروهی از هومومورفیسم های فضای خطوط را تشکیل می دهد. از این رو همین گروه گروهی از خودهمجنس گویی گروه موبیوس را که در پاراگراف قبل شرح داده شد ، تشکیل می دهد. اما هیچ معیاری در فضای خطوط هواپیما وجود ندارد که تحت عملکرد این گروه از هومومورفیسم ها ثابت باشد. از این نظر ، فضای خطوط در هواپیما هیچ متریک طبیعی بر روی آن ندارد. این بدان معنی است که گروه موبیوس دارای یک گروه طبیعی 4 بعدی Lie از خود همومورفیسم است که توسط ${\ displaystyle GL (2 ، \ mathbb {R})}$ ، اما این درجه بالای تقارن را نمی توان به عنوان گروه ایزومتری هر متریک نشان داد.

باند موبیوس با مرز گرد [ ویرایش ]

لبه یا مرز یک نوار موبیوس هومومورفیک (معادل توپولوژیک) یک دایره است . در قسمت تعبیه شده معمول نوار در فضای اقلیدسی ، مانند بالا ، مرز یک دایره واقعی نیست. با این حال ، می توان یک نوار موبیوس را به صورت سه بعدی تعبیه کرد تا مرز یک دایره کامل باشد که در یک سطح قرار دارد. به عنوان مثال ، به شکل 307 ، 308 و 309 "هندسه و تخیل" مراجعه کنید. [14]

همانطور که توسط بلین لاوسون کشف شده است ، یک جاسازی هندسی بسیار بیشتر با یک بطری کلین غوطه ور در 3 کره شروع می شود . سپس نیمی از این بطری کلاین را می گیریم تا یک باند Möbius تعبیه شده در 3 کره (واحد واحد در 4 فضای) بدست آوریم. نتیجه را گاهی اوقات "باند سودانی موبیوس" می نامند ، [15] که در آن "سودان" نه به کشور سودان بلکه به نام دو توپولوژیست ، سو گودمن و دانیل آسیموف اشاره دارد. استفاده از طرح stereographic به مکان های باند سودان آن را در فضای سه بعدی، به عنوان در زیر مشاهده می - یک نسخه با توجه به جورج فرانسیس را می توان یافت در اینجا .

از حداقل کلاین لاوسون بطری ما تعبیه باند به استخراج 3-حوزه S 3 ، به عنوان زیر مجموعه ای از C 2 است که هندسی همان R 4 . ما از طریق زاویه η ، φ را به اعداد مختلط z 1 ، z 2 رسم می کنیم

$z_ {1} = \ sin \ eta \ ، e ^ {i \ varphi}$

$z_ {2} = \ cos \ eta \ ، e ^ {i \ varphi / 2}.$

در اینجا پارامتر η از 0 تا π و φ از 0 تا 2 π اجرا می شود . از آنجا که | z 1 | 2 + | z 2 | 2 = 1 ، سطح تعبیه شده کاملا در S 3 نهفته است . مرز نوار توسط | داده می شود z 2 | = 1 (مربوط به η = 0 ، π ) ، که به وضوح یک دایره در 3 کره است.

برای به دست آوردن کدهای جاسازی از نوار موبیوس در R 3 یکی نقشه S 3 به R 3 از طریق یک طرح stereographic . نقطه فرافکنی می تواند هر نقطه از S 3 باشد که روی نوار تعبیه شده Möbius قرار نگیرد (این امر باعث حذف کلیه نقاط معمول طرح ریزی می شود). یک انتخاب ممکن این است $\ چپ \ {1 / {\ sqrt {2}} ، i / {\ sqrt {2}} \ راست \}$ . پیش بینی های استریوگرافی ، دایره ها را به دایره ها ترسیم می کند و مرز دایره ای نوار را حفظ می کند. نتیجه جاسازی صاف نوار موبیوس در R 3 با لبه دایره ای و بدون تقاطع های شخصی است.

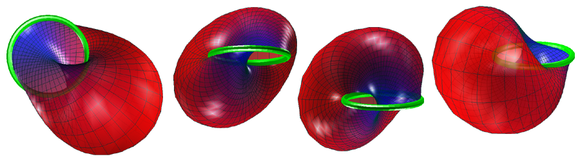
باند سودانی Möbius در سه کره S 3 از نظر هندسی یک بسته فیبر بر روی یک دایره بزرگ است که الیاف آن نیم دایره های عالی هستند. متقارن ترین تصویر از یک طرح کلیشه ای از این باند به R 3 با استفاده از یک نقطه فرافکنی که روی آن دایره بزرگ قرار دارد و از وسط هر یک از نیم دایره ها عبور می کند ، بدست می آید. هر انتخاب چنین نقطه فرافکنی منجر به ایجاد تصویری می شود که با تصویر دیگر مطابقت داشته باشد. اما از آنجا که چنین نقطه ای از خود بر روی باند موبیوس قرار دارد ، دو جنبه تصویر به طور قابل توجهی متفاوت از مورد است (که در بالا نشان داده شده است) که نقطه روی باند نیست: 1) تصویر در R 3باند کامل Möbius نیست ، بلکه باند با یک نقطه حذف شده است (از خط مرکزی آن). و 2) تصویر نامحدود است - و هرچه از مبدا R 3 فاصله می گیرد ، به طور فزاینده ای یک صفحه را تقریب می بخشد. با این حال این نسخه از تصویر استریوگرافی دارای یک گروه 4 تقارن در R 3 است (نسبت به گروه 4 کلاین یکسان نیست ) ، در مقایسه با نسخه محدود که در بالا نشان داده شده است و گروه تقارن آن گروه منحصر به فرد از مرتبه 2 است. (اگر تمام تقارن ها و نه فقط ایزومتری های جهت دار R 3 مجاز است ، تعداد تقارن ها در هر حالت دو برابر می شود.)

اما از نظر هندسی متقارن ترین نسخه ، باند اصلی Möbius سودان در سه کره S 3 است ، جایی که گروه کامل تقارن آن با گروه دروغ O (2) یکدست نیست. با داشتن یک کاردینالیته نامحدود ( پیوستار ) ، این به مراتب بزرگتر از گروه تقارن هرگونه تعبیه احتمالی باند Möbius در R 3 است .

منبع

https://en.wikipedia.org/wiki/M%C3%B6bius_strip

مشخصات وب

در این وبلاگ به ریاضیات و کاربردهای آن و تحقیقات در آنها پرداخته می شود. مطالب در این وبلاگ ترجمه سطحی و اولیه است و کامل نیست.در صورتی سوال یا نظری در زمینه ریاضیات دارید مطرح نمایید .در صورت امکان به آن می پردازم. من دوست دارم برای یافتن پاسخ به سوالات و حل پروژه های علمی با دیگران همکاری نمایم.در صورتی که شما هم بامن هم عقیده هستید با من تماس بگیرید.
09132003030

ریاضیات

آموزش ریاضی