ریاضیات

مقدمه تئوری گراف

EMAT 6690

یاماگوچی ، ژوئن-ایچی

در ترم تابستان سال 2005 ، من دوره ریاضیات را با عنوان "تئوری گراف (MATH6690)" می گذرانم. این دوره سخت اما بسیار جالب است و چشم من را به دنیای جدید ریاضی باز می کند.

من عاشق مطالعه تئوری گراف هستم و واقعاً می خواهم این ریاضیات بسیار جوان را بخوانید.

این رشته از ریاضیات را می توان برای بسیاری از موضوعات استفاده کرد ، از تحقیقات عملیاتی و شیمی گرفته تا ژنتیک و زبانشناسی و از مهندسی برق و جغرافیا گرفته تا جامعه شناسی و معماری.

تئوری گراف چیست؟

تئوری گراف مربوط به رابطه بین خطوط و نقاط است.

یک گراف از برخی نقاط و چند خط بین آنها تشکیل شده است.

به موقعیت نقاط و طول خطوط توجهی نمی شود.

بنابراین ، دو گراف زیر گراف یکسانی هستند.

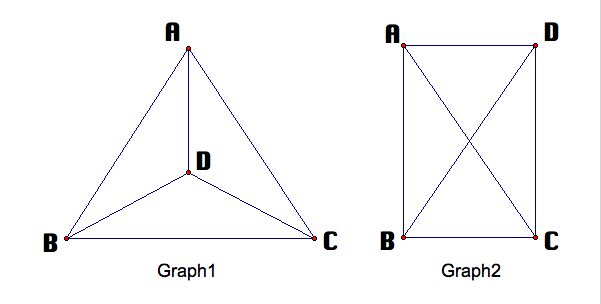
اصطلاحات اساسی تئوری گراف

ساده G گراف یک رضایت بخش است که است.

(1) داشتن حداکثر یک لبه (خط) بین هر دو رئوس (نقطه) و ،

(2) نداشتن لبه به راس اصلی.

من دو نمونه از گرافها را نشان می دهم که ساده نیستند.

مثال: این گراف ساده نیست زیرا دارای لبه ای نیست که راضی کننده باشد (2). لبه یک حلقه است.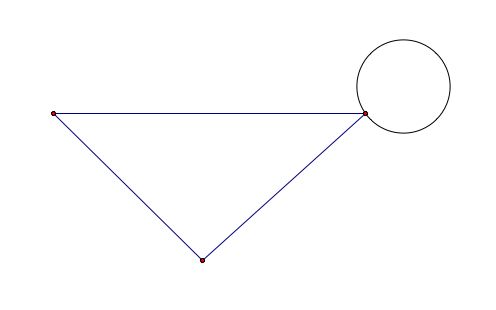

مثال: این گراف ساده نیست زیرا دارای 2 لبه بین رئوس A و B است.

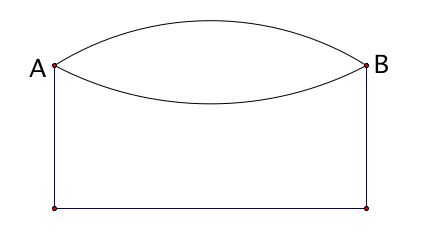
اگر یک لبه ، vx وجود داشته باشد ، دو رئوس v و w یک گراف مجاور هستند . سپس رئوس در نظر گرفته می شود INCIDENT به لبه ، vx.

درجه یک راس v از یک گراف تعداد یالهای با پنجم است.

مثال: درجه هر راس در این گراف زیر با تعداد نشان داده شده است.

تمرین 1

همه شش گراف ساده با 4 راس را پیدا کنید.

پاسخ

تمرین 2

dgree هر راس گراف زیر را پیدا کنید.

پاسخ

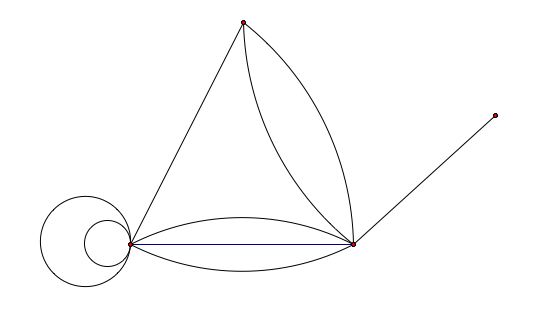
برخی از مسائل جالب در تئوری گراف.

من در تئوری گراف سه مسئله را نشان می دهم که جالب و اساسی هستند.

1. دست دادن لما (اساساً به دلیل لئونارد اولر در سال 1736)

اگر چند نفر با هم دست بدهند ، پس مجموع دستهای لرزان شده چقدر است؟

(توجه داشته باشید که تعداد مصاحبه ها نیست.)

وقتی برای بیان این سوال از برخی اصطلاحات نظریه گراف استفاده می کنیم ، می توان یک راس و یک لبه را به ترتیب یک شخص و یک مصافحه در نظر گرفت.

از آنجا که یک لبه با 2 راس اتفاق می افتد (توجه داشته باشید که G ساده است) ، به راحتی می توانیم ببینیم که 1 دست دادن از 2 نفر تشکیل شده است ، یعنی 2 دست.

نتیجه این است که تعداد کل لرزش دست ها دو برابر تعداد لرزش ها است.

متأسفانه ، ما نمی توانیم تعداد دقیق دستهای تکان داده شده را تشخیص دهیم زیرا از تعداد دست دادن اطلاع نداریم.

تنها چیزی که می دانیم این است که تعداد دست های لرزیده یکنواخت است.

از نظر تئوری گراف ، در هر گراف مجموع تمام راس-درجه ها یک عدد زوج است - در واقع ، دو برابر تعداد لبه ها.

علاوه بر این ، می توانیم بگوییم که در هر گراف تعداد رئوس درجه فرد زوج است.

2. گرافهای اولریایی

یک مسئله معمول را در نظر بگیرید که آیا می توان بدون برداشتن مداد از روی کاغذ و بدون تکرار خطوط ، گراف مشخصی ترسیم کرد: (رسم یک تصویر با یک ضربه(

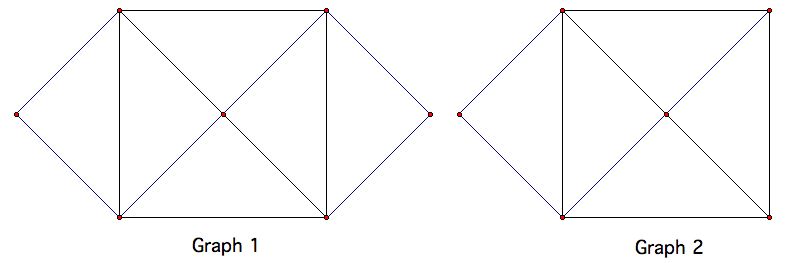
مشکل: کدام یک از گرافهای 1 ، 2 و 3 زیر را می توان با یک بار کشیدن ترسیم کرد؟

aaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaa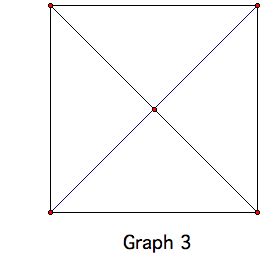

پاسخ:

گرافهای 1 و 2 را می توان به روش دلخواه ترسیم کرد ، اما گراف 3 نمی تواند.

آیا تفاوت بین رسم گراف 1 و گراف 2 را دیدید؟

با توجه به نقاشی های یک زمانه گراف 1 ، نقطه پایان همان نقطه شروع است. در مقابل ، نقشه های یک زمانه گراف 2 شروع و پایان متفاوتی دارند.

مانند گراف 1 بالا ، اگر یک گراف راهی برای رسیدن از یک راس به دیگری داشته باشد که دقیقاً یک بار شامل هر لبه شود و به راس اولیه ختم شود ، گراف آن اولریایی است (یک گراف اولریایی است).

مانند گراف 2 در بالا ، اگر یک گراف دارای راه هایی برای رسیدن از یک راس به دیگری باشد که دقیقاً یک بار شامل هر لبه باشد و به یک راس دیگر غیر از ابتدا شروع شود ، گراف نیمه اولری است (گراف نیمه اولری است).

نام 'اولریان' از این واقعیت ناشی می شود که ریاضیدان اولر اولین کسی است که مسئله معروف "مشکل پل های کونیگسببرگ" را حل کرد ، که به شما می گوید چگونه دقیقاً یکبار از هر 7 پل موجود در شکل زیر عبور کرده و به مرحله اصلی خود بازگردید. نقطه.

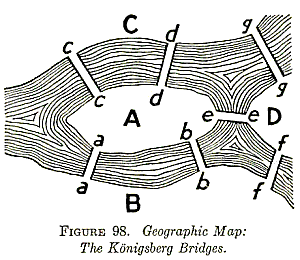
نمایی از کونیگسبرگ همانند روزهای اولر

این معادل پرسیدن این است که آیا گراف زیر یک دنباله اولریایی دارد ، این است که آیا گراف اولری است.

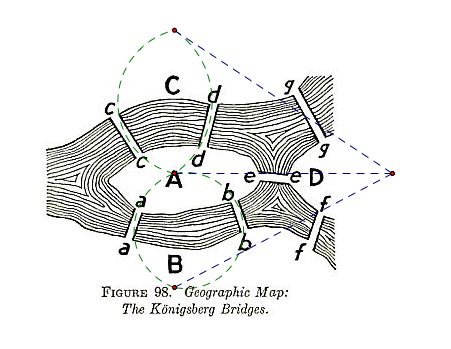
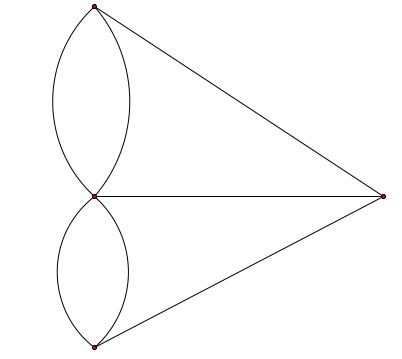
ورزش: سعی کنید دنباله اولری را در گراف Königsberg پیدا کنید.

امتحان کردی؟

من حدس می زنم که شما نمی توانید هیچ دنباله اولری پیدا کنید زیرا اولر از نظر ریاضی ثابت کرد که هیچ کس نمی تواند نقاشی یک ضربه ای روی آن گراف پیدا کند.

در اینجا معروف ترین و ساده ترین قضیه (اولر 1736) در مورد اینکه آیا گراف داده شده اولری است یا نه ، آمده است.

یک گراف متصل G ، اولریایی است اگر و فقط اگر درجه هر راس G یکنواخت باشد

با استفاده از این قضیه ، گراف مسئله پل های Königsberg حل نشدنی است.

3. گرافهای همیلتونی

در حالی که ما در بخش "گراف اولری" راهی را برای رفتن و بازگشت شامل هر لبه گراف در نظر گرفتیم ، ما در اینجا یک مشکل مشابه دور زدن روی گراف شامل هر "راس" (نه "لبه") را در نظر می گیریم.

مشکل: کدامیک از گرافهای 1 ، 2 و 3 زیر راهی برای عبور از هر راس دارد؟

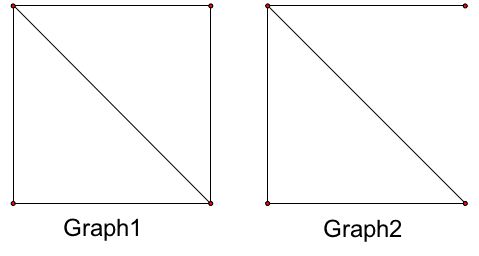
آاااااااااااااااا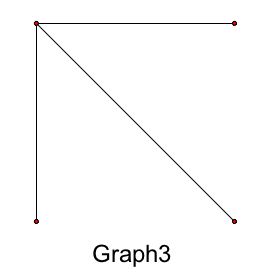

پاسخ:

گراف 1 و گراف 2 چنین روشی دارند (همانطور که در زیر نشان داده شده است) ، اما گراف 3 نه.

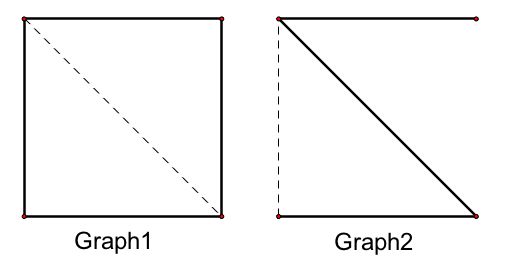
مشابه داستان گراف اولری ، بین نحوه گراف 1 و گراف 2 تفاوت وجود دارد. این مربوط به نقاط انتهایی مسیرها است.

با توجه به مسیر گراف 1 ، نقطه پایان همان نقطه شروع است. در مقابل ، مسیر گراف 2 شروع و پایان متفاوتی دارد.

مانند گراف 1 در بالا ، اگر گراف دارای مسیری باشد که دقیقاً یک بار شامل هر راس باشد ، در حالی که به راس اولیه ختم می شود ، گراف همیلتونین است (گراف همیلتونین است). به این مسیر "چرخه همیلتون" گفته می شود.

مانند گراف 2 در بالا ، اگر یک گراف مسیری داشته باشد که دقیقاً یکبار شامل هر راس باشد ، اما به انتهای دیگر نسبت به راس دیگر ختم شود ، گراف نیمه هامیلتونی است (گراف نیمه همیلتون است).

به یاد بیاورید که در بخش قبلی "اولریان" قضیه بسیار ساده و مفیدی راجع به اینکه آیا گراف اولری است یا نه ، دیدیم. از آنجا که متأسفانه ، به طور کلی درباره چرخه همیلتونی اطلاعات کمی در دست است ، یافتن چنین خصوصیاتی یکی از مشکلات حل نشده تئوری گراف است.

مسئله:

یک گراف همیلتونین از گراف زیر پیدا کنید.

یکی از پاسخ های این مشکل است

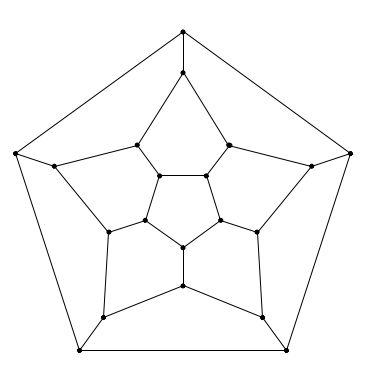
مسئله:

یک گراف همیلتونین از گراف زیر پیدا کنید.

(این مشکل کاملاً سخت است. با این حال ، این بدان معنا نیست که پاسخی وجود ندارد).

یکی از پاسخ های این مشکل است

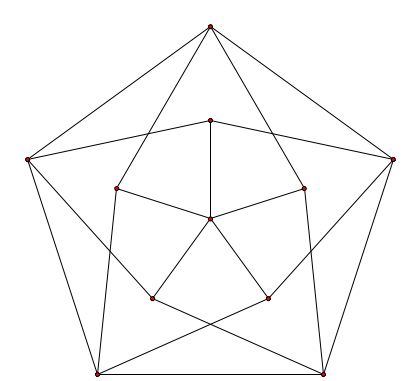
من برخی اصطلاحات و مفاهیم اساسی تئوری گراف را معرفی کرده ام.

من تقریباً توضیحات خود را برای معرفی تئوری گراف به پایان می برم.

اما بسیاری از موضوعات جالب توجه دیگر را نیز می توانم نشان دهم.

در اینجا من فقط لیستی از این مسائل را با پیوندها برای تعریف و توضیح درباره آنها ارائه می دهم.

برخی از موضوعات ارتباط قوی با سایر رشته های تحصیلی دارند.